![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。好奇心旺盛で根気強い《元気少女》。
ここは高校の図書室。いまは放課後。
僕は後輩のテトラちゃんとおしゃべりをしている。
テトラ「そういえば先輩は、アキレスと亀というお話はご存じですよね」
僕「もちろん知っているよ。有名なパラドックスだよね。 『アキレスは足が速いのに、足が遅い亀に追いつけない』 という話。明らかにまちがいなんだけど、 どこがまちがいなのか言い当てることが難しい。 まさにパラドックスだね」
テトラ「はい、それです」
僕「《アキレスと亀》のパラドックスを提示したゼノンは哲学的な話をいいたかったらしいけど、 そちらの方はよく知らない。 でも、少なくとも数学的には解決できる話だと思うよ。 テトラちゃんだったら、すぐにわかる」
テトラ「あっ、いえいえ、 あたしも《アキレスと亀》のパラドックスは知っています。 別にわからないというわけじゃないんです。 というか、ええとですね。わかっていると思っていたんですが……」
僕「?」
テトラ「先日、お友達とおしゃべりしていて数学の話になったんです。 あっ、女の子のお友達です」
僕「うん、それで?」
テトラ「その友達は、あたしのことを数学が得意だと思っていて、 この《アキレスと亀》の話をふってきたんです。 どこがおかしいか説明してほしいって」
僕「ああ、なるほど。テトラちゃんじゃなくて、 その友達が《アキレスと亀》をわからなかったということなんだね」
テトラ「はい……でも、説明しているうちに、 あたしまでよくわからなくなってしまったんです」
僕「へえ、でも、いちど理解したら、そんなに難しくないと思うんだけど」
テトラ「それで、先輩だったら《アキレスと亀》をどんなふうに説明なさるかなあ……って」
僕「なるほど。じゃあ、まず、そもそもの問題から考えてみようか」
テトラ「はいっ!」
僕「《アキレスと亀》の問題は、こういうものだね」
《アキレスと亀》の問題(1)
アキレスと亀が、走る競争(徒競走)をする。
アキレスは亀よりも足が速いのでハンディをつける。
亀は、アキレスの位置よりも前に出た位置から走り始める。
アキレスは亀よりも足が速いのに、亀を追い越すことができない。
その理由は以下の通り。
テトラ「はい、そうですね。よくわかります。 これが《アキレスと亀》のパラドックスです」
僕「この話、ユーリにもしたことがあるけど、 たいへんだったよ」
テトラ「何がたいへんなんでしょう」
僕「細かいツッコミが多かったんだよ。 たとえば、 『スタート地点を気にするのはいいけど、 ゴール地点は決めなくていいの? 競争なんだから、まずゴール地点を決めろよー』 とか『前ってどっち? アキレスがゴールに近かったら意味がない』 とかね」
テトラ「なるほどです」
僕「それはさておき、 この問題の表し方は考えにくいよね。 《最初に二人がいる位置》や、 《亀がいた位置》までアキレスがたどり着いたときの《亀の位置》のように、 いろんな位置が出てくるから、まぎらわしい。 《さっき亀がいた位置》や《そのときに亀がいる位置》のように指示語が多くなってしまうとややこしい。 数学的な表現をした方がわかりやすくなる」
テトラ「はい、そうですね」
《アキレスと亀》の問題(2)
数直線上を移動する二点 $A$ と $B$ がある。
以下、 $n = 1,2,3,\ldots$ という段階を踏んで話を進める。
各段階の点 $A$ の位置を $a_n$ で表す。
各段階の点 $B$ の位置を $b_n$ で表す。
【段階 $1$ 】
点 $A$ は、 $a_1 = 0$ の位置からスタートして速さ $1$ で正の向きに進むとする。
点 $B$ は、 $b_1 = 1$ の位置からスタートして速さ $\frac12$ で正の向きに進むとする(つまり、点 $B$ の速さは点 $A$ の半分の速さである)。
【段階 $2$ 】
点 $B$ を追い越すため、 点 $A$ は位置 $b_1$ まで進まなければならない。 このとき点 $A$ の位置は $a_2 = b_1$ となる。
点 $A$ が位置 $a_1$ から $a_2$ まで進むとき、 点 $A$ は距離 $a_2 - a_1 = 1$ だけ進んだことになる。 そのとき点 $B$ は点 $A$ が進んだ距離の半分($\frac12$)だけ進んでいることになるので、 点 $B$ は $b_2 = b_1 + \frac12$ の位置まで進んでいる。
【段階 $3$ 】
点 $B$ を追い越すため、 点 $A$ は位置 $b_2$ まで進まなければならない。 このとき点 $A$ の位置は $a_3 = b_2$ となる。
点 $A$ が位置 $a_2$ から $a_3$ まで進むとき、 点 $A$ は距離 $a_3 - a_2 = \frac12$ だけ進んだことになる。 そのとき点 $B$ は点 $A$ が進んだ距離の半分($\frac14$)だけ進んでいることになるので、 点 $B$ は $b_3 = b_2 + \frac14$ の位置まで進んでいる。
僕「ここまでは、いいよね?」
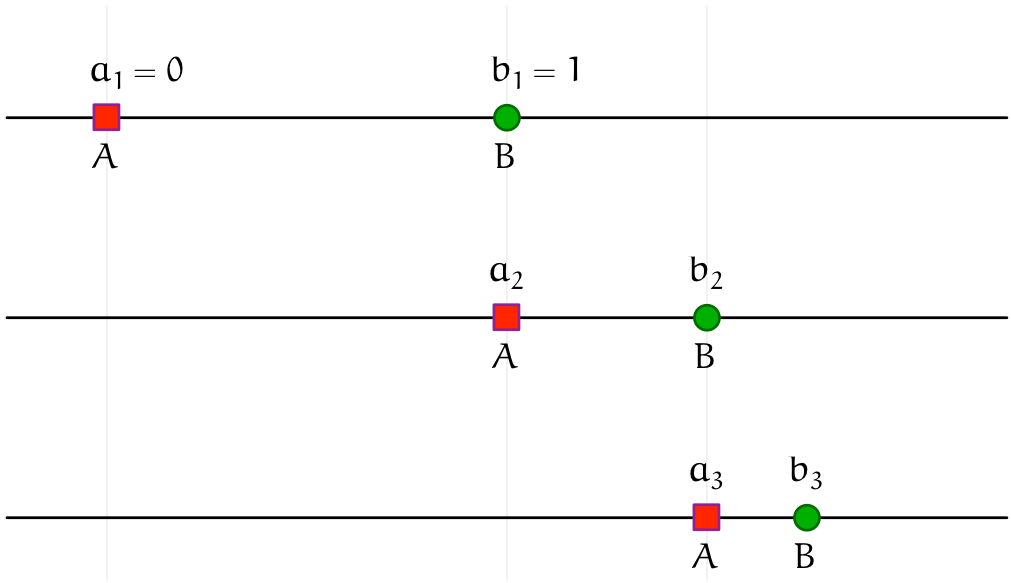
テトラ「は、はい。大丈夫です。点 $A$ がアキレスに相当して、 点 $B$ が亀に相当するということですよね。 なるほど段階 $n$ ですか……」
僕「うん。段階 $n$ のときはこうなっている」
【段階 $n$ 】
点 $B$ を追い越すため、 点 $A$ は位置 $b_{n-1}$ まで進まなければならない。 このとき点 $A$ の位置は $a_{n} = b_{n-1}$ となる。
点 $A$ が位置 $a_{n-1}$ から $a_{n}$ まで進むとき、 点 $A$ は距離 $a_{n} - a_{n-1} = \frac{1}{2^{n-1}}$ だけ進んだことになる。 そのとき点 $B$ は点 $A$ が進んだ距離の半分($\frac{1}{2^n}$)だけ進んでいることになるので、 点 $B$ は $b_{n} = b_{n-1} + \frac{1}{2^{n}}$ の位置まで進んでいる。
テトラ「……」
僕「だから、段階 $n$ がいくら進んでも、点 $B$ の位置 $b_n$ は点 $A$ の位置 $a_n$ よりも、 $$ \frac{1}{2^{n}} $$ だけ前に進んでいることになる。 つまり、どんな正の整数 $n$ に対しても、 $$ a_{n} < b_{n} $$ が成り立つことになる。したがって、 いつまでたっても、点 $A$ は点 $B$ を追い越せない。 これがパラドックスに見える問題」
テトラ「先輩!」
僕「どうしたの?」
テトラ「これって、この《アキレスと亀》の問題って、 数学的帰納法で証明できてしまいませんか? だって、数学的帰納法は 《どんな正の整数 $n$ に対しても、 数学的主張 $P(n)$ が成り立つことを証明する証明法》ですよね?」
僕「ああ、もちろん証明できるよ。《ステップA》と《ステップB》を踏めばいいからね」
テトラ「でも! 証明できてしまったらパラドックスになってしまいますっ!」
僕「パラドックスに見えるけど、パラドックスじゃないよ」
テトラ「え、ええと……」
僕「テトラちゃんが心配しているのはこういうことだよね?」
テトラちゃんの心配
《アキレスと亀》の問題(2)について、どんな正の整数 $n$ に対しても、 $$ a_{n} < b_{n} $$ が成り立つことは、数学的帰納法で証明できる。
点 $A$ の位置 $a_n$ はアキレスを表し、点 $B$ の位置 $b_n$ は亀を表している。
したがって、アキレスはいつまでも亀を追い越すことはできない。
テトラ「そうです……どうなるんでしょうか」

僕「それはね、数学的帰納法で証明できることは何かを確かめればはっきりするんだよ」
テトラ「数学的帰納法で証明できること?」
僕「うん。さっきの話をちゃんと数学的帰納法で証明してみよう。こうなるよ」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2018年2月16日)