![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
ユーリと僕は、 $$ \frac17 = 0.142857142857\cdots = 0.\dot14285\dot7 $$ という数を使って楽しくおしゃべりをしている(第213回参照)。
ユーリ「そーいえば、エジプトもこれだったね」
僕「これって?」
ユーリ「$\frac17$ みたいな分数を考えるんじゃなかったっけ」
僕「単位分数のことだね。 分子が $1$ になっている分数の和の形で数を表した」
ユーリ「それそれ。《いにしえの数学》イベントで見た(第182回参照)」
僕「古代エジプトだと、分子が $1$ になっている分数と、 それから $\frac23$ が基本的な数として使われたんだね。 たとえば、 $\frac{3}{5}$ という数を表すときには、 $$ \frac{1}{3} + \frac{1}{5} + \frac{1}{15} $$ に相当する書き方をする」
ユーリ「クラゲみたいなの」
僕「クラゲというか、雲というか……」
古代エジプトの文字(ヒエログリフ)で書いた $\frac{1}{3} + \frac{1}{5} + \frac{1}{15}$
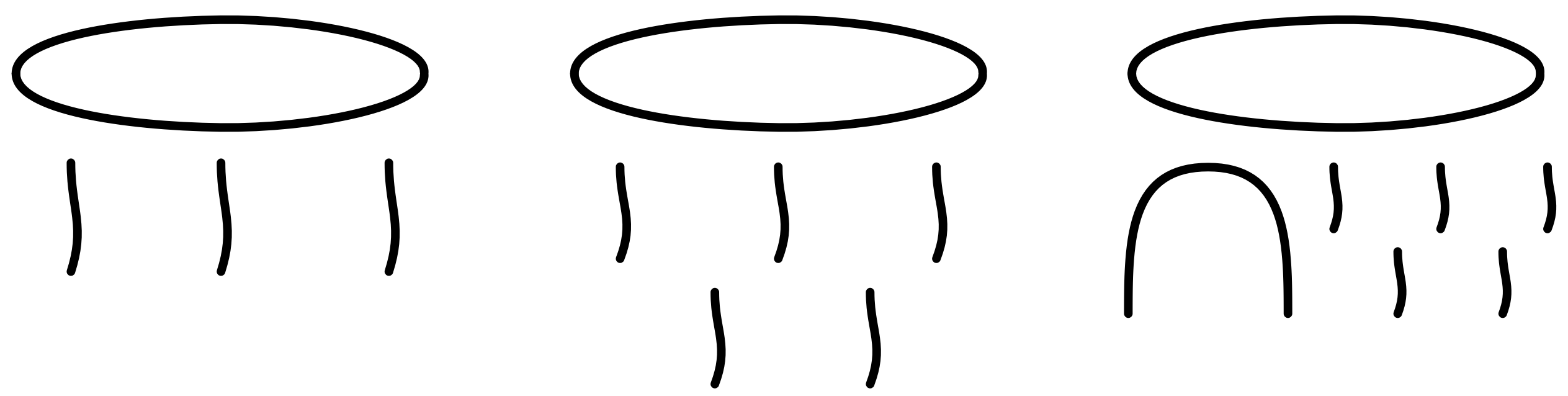
ユーリ「めんどいよね。 だって $\frac{3}{5}$ って書けばいいだけなのに、 わざわざ並べて足し算にするなんて」
僕「古代エジプトの人はそれで慣れていたのかもしれないけどね。 数の表記法には一長一短あるから」
ユーリ「ひょうきほう? いっちょういったん?」
僕「《数の表記法》、つまり《数を書き表すやり方》によって、 便利な場合と不便な場合が変わるってこと」
ユーリ「ちょっと何言ってるかわかんない」
僕「たとえば、さっきの話に出てきた $\frac17$ は分数で書いたけど、 小数で書くこともできる。 $\frac17$ と書く代わりに、 $0.\dot14285\dot7$ と書く」
$$ \frac17 = 0.\dot14285\dot7 $$ユーリ「そだね」
僕「いまの二つの書き表し方、つまり表記法は違う。 でも、その二つはイコールで結べる。 $\frac17$ と $0.\dot14285\dot7$ とは、異なる表記法で書かれているけれど、 値は等しいんだよということを表している」
ユーリ「まわりくどい言い方」
僕「でも、大事なことなんだよ。ある数を書き表したいと思ったときに、 分数の形で表すなら $\frac17$ と書くし、 小数の形で表すなら $0.\dot14285\dot7$ と書く。 古代エジプト人がヒエログリフで表すなら $7$ を表すヒエログリフの上に雲みたいなものを描いたかもしれない。 でも、表記法が違うだけで値は等しい」
ユーリ「それで? いっちょういったん」
僕「うん。 $\frac17$ の形で書くと、 $1$ を $7$ で割った値だなということがわかりやすい。 でも、ほら、さっき調べたような $142857$ の繰り返しが出てくるというパターンを調べるは $\frac17$ という表記法ではわかりにくい」
ユーリ「ふむふむ。パターンね」
僕「それから、大きさを比べるときも考えてみよう。 $\frac{7}{13}$ と $\frac{11}{21}$ ではどっちが大きい?」
クイズ1(どちらが大きいか?)
$$ \frac{7}{13} \qquad \REMTEXT{と} \qquad \frac{11}{21} $$
ユーリ「えっと?」
僕「こういう分数同士だと、パッと見て大きさの比較は難しい。 でも、小数で表されていれば、 $0.\dot53846\dot1$ と $0.\dot52380\dot9$ のどちらが大きいかはすぐわかる」
クイズ2(どちらが大きいか?)
$$ 0.\dot53846\dot1 \qquad \REMTEXT{と} \qquad 0.\dot52380\dot9 $$
ユーリ「$0.\dot53846\dot1$ の方が大きい! だって、 左は $0.53\cdots$ だけど、右は $0.52\cdots$ だから」
僕「そうなんだ。小数で表すと、二つの数の大小関係はいつもわかりやすい。 それに比べて分数だと大きさの比較が難しいことがある」
ユーリ「なるほどー。あ、でも、簡単なときもあるよ」
僕「そうだね。分数の大小比較がいつも難しいとは限らない。分母が等しかったり、 分子が等しかったりすれば比較は簡単」
ユーリ「分母は大きくて分子が小さいとかね」
僕「そういうこと」
ユーリ「単位分数同士なら、分子がいつも $1$ だから比較は楽だね」
僕「なるほど。確かにそれはいえるな。 ともかく、値と表記法の区別は大事だし、 表記法ごとに便利な点は違うというのは納得できた?」
ユーリ「ナットク、ナットク」
僕「そういえば、小学校のときに《分数を小数に直す計算》や《小数を分数に直す計算》をたくさんやったよね」
ユーリ「やったやった。超めんどいの」
僕「あれは、《数の値は変えずに、表記法を変える》という練習だったんだね。 分数には分数の、小数には小数の便利なところがある。 だから、自分の都合がいい表記法に書き換えるのは大事なこと。 でも、書き換える途中で値を変えちゃだめだよね。 さっきのクイズ1,2も同じ問題なんだけど、表記法が違うだけ。 $$ \begin{align*} \frac{7}{13} &= 0.\dot53846\dot1 \\ \frac{11}{21} &= 0.\dot52380\dot9 \\ \end{align*} $$ だから、 $$ \frac{7}{13} = 0.\dot53846\dot1 > 0.\dot52380\dot9 = \frac{11}{21} $$ ということ」
ユーリ「ふむふむ」
クイズ1とクイズ2の答え
$$ \frac{7}{13} = 0.\dot53846\dot1 > 0.\dot52380\dot9 = \frac{11}{21} $$
ユーリ「あれ? お兄ちゃん。逆は?」
僕「《ならば》は出てきてないよ」
ユーリ「その逆じゃなくて、反対は?」
僕「ねえ、ユーリ。テレパシーで会話するのはやめようよ。 何の話か順序立てて言ってくれないとわからないよ」
ユーリ「察し悪いのう。あのね、 $\frac{1}{7}$ を小数で表すと、 $$ \frac17 = 0.\dot14285\dot7 $$ になるんでしょ?」
僕「そうだね。もちろん、 $0.142857142857\cdots$ と表してもいいけど。それで?」
ユーリ「小数に直すとどうなるかは、 $1$ を $7$ で割ればわかるじゃん?」
$\frac17$ を小数に直す
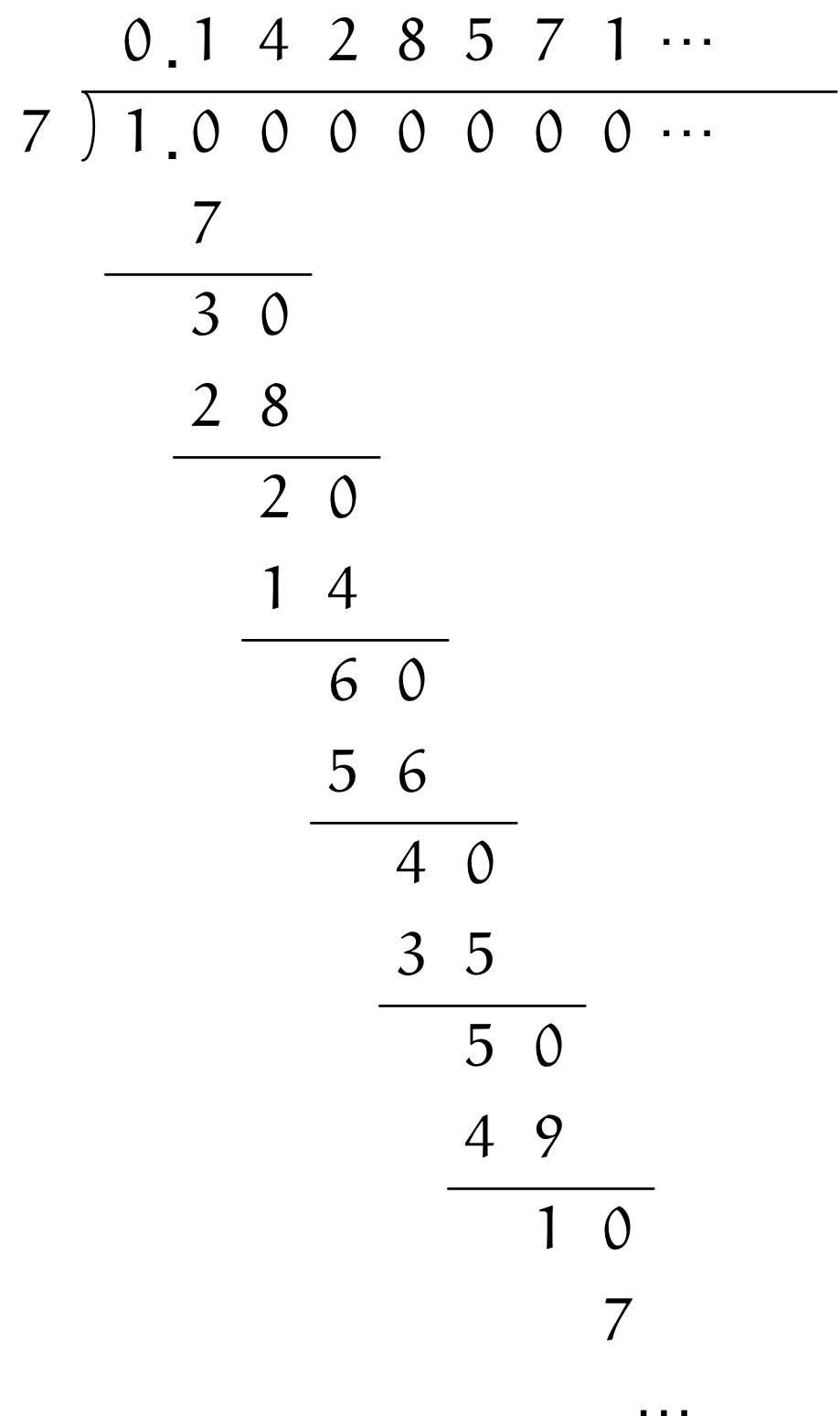
僕「そうだね」
ユーリ「だから、その逆は? $0.\dot14285\dot7$ を見たとき、 $\frac17$ ってすぐわかる? 小学校で習ったっけ?」
僕「なるほど! 《$0.\dot14285\dot7$ という小数を分数に直す》にはどうするかという問題だね」
ユーリ「そーゆーことじゃ。 あっ、もちろん $\frac17$ になるのはもう知ってるからわかるよ。 でもたとえば、適当に、 $$ 0.123123123\cdots = 0.\dot12\dot3 $$ みたいな小数を作ったら、これって分数にできるの? $0.123$ じゃないくて、 $0.\dot12\dot3$ だよ? お兄ちゃん、暗記してる?」
僕「いや、暗記はしてないし、小学校で習った覚えもないけど、 これは考えれば解ける問題だよ」
問題(無限小数を分数に直す)
次の無限小数を分数で表せ。 $$ 0.123123123\cdots = 0.\dot12\dot3 $$

ユーリ「《あなたも、考えてみましょう!》のカンバン、出ちゃった」
僕「メタ発言自重……考え方は難しくないと思うけど」
ユーリ「うーん。 $0.123$ だったら楽なんだけど」
僕「それだよ、ユーリ。ポリヤの問いかけ《似た問題を知らないか》だね。 ユーリは $0.\dot12\dot3$ を分数に直す方法は知らない。でも、 $0.123$ を分数に直す方法という似た問題なら解ける」
ユーリ「だって、 $$ 0.123 = \frac{123}{1000} $$ でしょ? 約分はできない」
僕「そうだね。いまは約分は気にしなくていいよ。ともかく、 $0.123$ はすぐに分数にできた。でも $0.\dot12\dot3$ は分数にできない。 その二つは何が違うんだろう」
ユーリ「$0.\dot12\dot3$ は $123$ が無限に続いているから。 $\frac{123}{1000}$ だけじゃ足りないでしょ?」
僕「……」
ユーリ「むむ? さては、その無言は《ヒントの無言》だにゃ? お兄ちゃんの目が語ってる! 『そこがポイントだよ。じっくり考えてごらん、かわいいユーリ』って語ってる!」
僕「《求めたいものは何か》」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2017年12月1日)