第202回 シーズン21 エピソード2

最初に最後を考えて（後編）

僕の部屋

僕「うん、だからね。 $1,-1,1,-1,\ldots$ のように $1$ と $-1$ が交互に現れる数列は、 $(-1)^n$ と表すこともできるし、 $(-1)^{n+2}$ と表すこともできるし、 $\cos n\pi$ と表すこともできるし、 $\sin \left(n\pi + \frac{\pi}{2}\right)$ と表すこともできる。 どれが正しいなんてことはないんだよ」

ユーリ「えー、 でもいきなりコサインで書く人はいないんじゃない？」

僕「確かにね。 $(-1)^n$ はシンプルでわかりやすいから」

ユーリ「そーだよ。わざわざ三角関数で……」

僕「ああ、でも、ミルカさんがおもしろいこと言ってたなあ。 『数列も関数だよ』って」

ユーリ「いまの、ミルカさまのモノマネのつもり？　あんま似てない」

僕「いや……そういうわけじゃないよ。 ともかく、数列は関数と考えることができる。数列は関数の一種だという話をしてたんだ」

ユーリ「数列って、関数なの？」

僕「納得いかない？」

ユーリ「だって、数列って数が並んでるものじゃん？　 でも、関数は……関数は……」

僕「関数は？」

ユーリ「関数は、わかんないけど、 もっとヒュンとしてる。ギュインって」

僕「なんだそりゃ」

ユーリ「だって、関数ってグラフみたいなものじゃん？　 ヒュンと直線だったり」

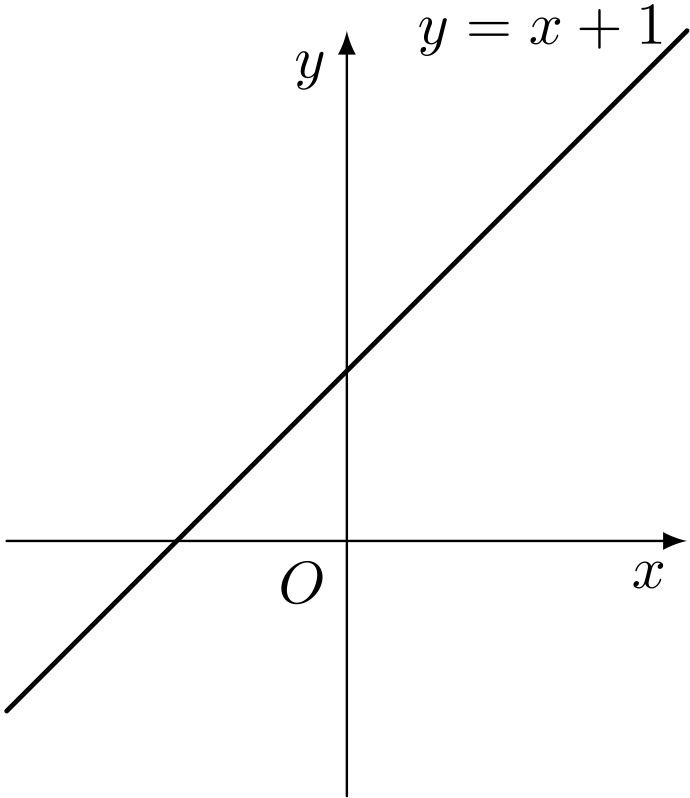
僕「ギュインって放物線だったり？」

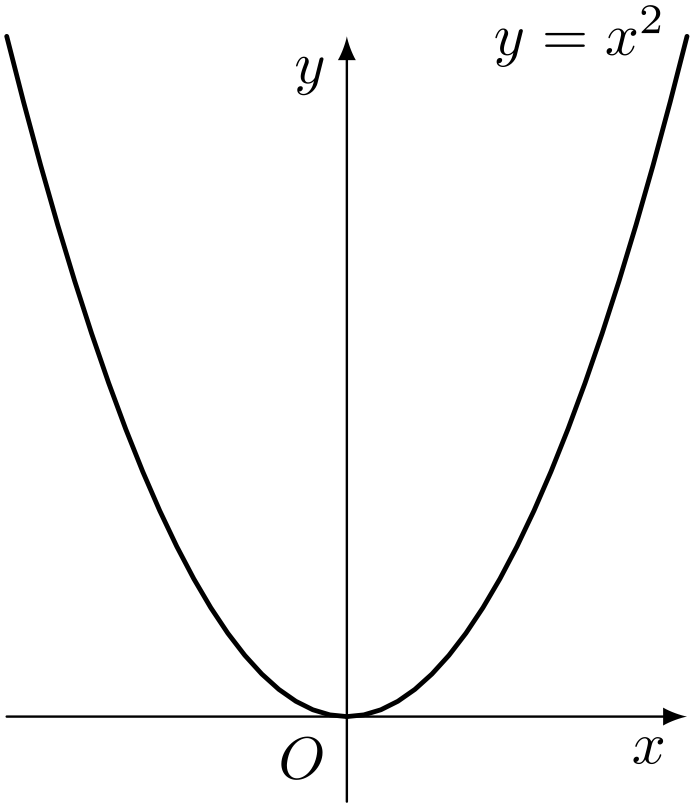
ユーリ「そーそー、そゆこと」

僕「確かに、 関数をグラフで表すというのはよくやることだね。 そして関数をグラフで表したときに直線や放物線になることも、もちろんある。 そこまではユーリは正しいよ」

ユーリ「うんうん。そーだ！　関数って $f(x)$ みたいなの！」

僕「そうだね。 $x$ の関数のことを $f(x)$ と表すこともある。 それも正しい。でもね、《関数とは何か？》って改めて聞かれたら、 ユーリはなんて答える？」

ユーリ「関数とは、何か……」

僕「そうだね。 つまり、関数の定義を聞かれていることになる」

ユーリ「関数の定義！　関数に定義なんてあるの？」

僕「そりゃあるよ。そうでなくちゃ、 関数についてきちんと考えることは難しいよね。 どんなものなら関数と呼ぶことができるか。 どんなものは関数と呼べないか。 それをはっきりさせてくれるのが定義だからね」

ユーリ「関数の定義なんて考えたこともなかったよー」

僕「だったら、いまが考えるチャンスだね」

ユーリ「『いまでしょ！』とか言わないの？」

僕「言わない」

$y = x + 1$ を考える

僕「関数を定義する前に、関数の例を見てみようか。 さっきユーリは直線とか放物線とかいってたよね」

ユーリ「うん。グラフ」

僕「たとえば、これは $y = x + 1$ という式で表されるグラフだよね」

ユーリ「そーそー、こーゆーの。これは直線でしょ？」

僕「そうだね。このグラフは直線になっていて、 $y = x + 1$ という式で表されている。 このグラフで $x$ の値が $0$ のとき、 $y$ の値は何になる？」

ユーリ「$x$ が $0$ なら、 $y$ は $1$ でしょ？ $x$ に $1$ 足せば $y$ だもん」

僕「そうだね、正解。 じゃあ、 $x$ の値が $5$ のとき、 $y$ の値は何になる？」

ユーリ「$1$ 足すから $6$」

僕「うん。それでいいよ。このグラフで $x = 5$ のとき $y = 6$ だ」

ユーリ「カンタン。そんで？」

僕「だったら、 $x = -12345$ だったら？」

ユーリ「いきなりマイナス！　えーと、 $y = -12344$ かにゃ？」

僕「そうだね。 $y = x + 1$ なんだから、 $x = -12345$ のときは $y = -12345 + 1 = -12344$」

ユーリ「難しくない」

僕「次は難しいよ。 $x$ の値がユーリだったら、 $y$ の値は？」

ユーリ「は？　なに言ってるですか？　$x = \REMTEXT{ユーリ}$なんてありえないじゃん」

僕「それはどうしてだろう」

ユーリ「ユーリは数じゃないもん！　 $\REMTEXT{ユーリ} + 1$なんて計算できない！」

僕「そうだね。このグラフの $x$ 軸にユーリは出てこないし、 犬も猫も出てこない」

ユーリ「おどろいちゃった」

僕「さっきから、 $y = x + 1$ というグラフを使って、 《$x$ の値がナントカのとき、 $y$ の値はナニになる？》 と聞いたけれど、この質問に答えるのが関数なんだよ」

ユーリ「何それ突然！」

関数の定義

僕「関数の定義をきちんと書くとこうなるよ、ユーリ」

ユーリ「意味わかんない」

僕「がく。ちゃんと読んだ？」

ユーリ「何となくわかるけど、わざとややこしく書いてない？」

僕「いやいや、抽象的だけど、ややこしくはないよ。イメージがわかりにくいかったら、こんな図はヒントになるよ」

ユーリ「どっちにしても、よくわかんない」

僕「確かに、定義は抽象的に見えることが多いかもね。 だからこそ、定義を見たときには具体例を作ることが大事なんだ。 ほら、《例示は理解の試金石》だから」

ユーリ「《例示は理解の試金石》だし《礼儀は社会の潤滑油》だよね」

僕「ちゃかさない。関数の定義を $y = x + 1$ に照らし合わせてみよう」

ユーリ「へーい」

僕「さっき僕たちは $y = x + 1$ というグラフで、 関数のことをぼんやりと考えたけど、 関数の定義に合わせてきちんと表してみよう」

ユーリ「ほほー」

僕「僕たちは $y = x + 1$ のグラフを考えるとき、 どんな実数 $x$ に対しても、実数 $y$ が対応付けられていると考えるよね」

ユーリ「それって、 $x$ に対して $y$ は $x + 1$ になるってこと言ってるの？」

僕「そうだよ。実数 $x$ に対して実数 $y$ がたった一つ決まる。 $y$ を決める約束、ルール、対応付け、規則が決まっている。 その規則のことを関数と呼ぶんだ」

ユーリ「はあ」

僕「さっきの《関数の定義》では最初に、 《二つの集合 $X$ と $Y$ を考える》 といってたけど、 $y = x + 1$ のときには集合 $X$ も $Y$ もどちらも《実数全体の集合》としていいよ」

ユーリ「実数全体の集合……」

僕「うん。 $y = x + 1$ のグラフを考えるとき、 $x$ 軸上のどんな点 $x$ を選んでも対応する $y$ が一つ決まった。 $x$ 軸上の点を一つ選ぶというのは、 実数を一つ選んでいるということ。 そしてそれに対して $y$ が決まるけど、 これは $y$ 軸上の点つまり実数を一つ決めていることになる」

ユーリ「まわりくどいけど、いーよ」

僕「しかも、 $y = x + 1$ というグラフでは、 実数 $x$ に対して実数 $y$ がたった一つだけ決まる。つまり……

• $x$ に対して、 $y$ が決まらないということはない。
• $x$ に対して、 $y$ が二つ以上決まるということもない。
• $x$ に対して、決まった $y$ が実数以外ということもない。

ユーリ「おー！　あたりまえで、めちゃめちゃくどいけど、確かに」

僕「どんな実数 $x$ に対しても、実数 $y$ がたった一つだけ対応して必ず決まる。 その対応の規則は、 さっきの例では $y = x + 1$ という式で表されていた。 もしもこの規則に $f$ という名前を付けるとしたら、 $$ y = x + 1 $$ のことを、 $$ y = f(x) $$ と書ける」

ユーリ「解説、乙。 でもにゃあ……あたりまえにわかってることを回りくどく言ってるみたい」

僕「まあね。でも、関数の定義で、 集合 $X$ と集合 $Y$ をきちんと決めておくことが大事だとわかるよね。 さっきの『$y = x + 1$ で $x$ の値がユーリだったら $y$ の値は何？』 という質問が無意味なのは、ユーリが実数じゃないからなんだよ」

ユーリ「はあ」

僕「関数 $f$ の定義に出てくる集合 $X$ のことを定義域というんだ」

ユーリ「ていぎいき」

僕「$f$ が関数なら、定義域にある要素 $x$ を選んだとき、 対応する値が一つ定まることが保証される。 それを $f(x)$ で表すんだね」

ユーリ「うーん……ねえお兄ちゃん。説明はわかったけど、 飽きてきちゃった。だって、何だかぜんぶあたりまえみたいなんだもん」

僕「うん、関数の定義はこのくらいにして、さっきの話に戻ろう」

ユーリ「さっきの話って何だっけ？」

僕「数列も関数だよ、って話」