第169回 シーズン17 エピソード9

広がりを求めて（前編）

僕の部屋

ユーリ「ねーお兄ちゃん、こないだ複素数の話してたよね。 複素数とゆーか、複素平面。複素数という《数》を《点》で表す話」

僕「うん、そうだね（第164回参照）」

ユーリ「あれって平面じゃん？　二次元の世界」

僕「そうだね」

ユーリ「だったら、複素数は《二次元の数》と呼べる？」

僕「うん、呼んでかまわないと思うよ」

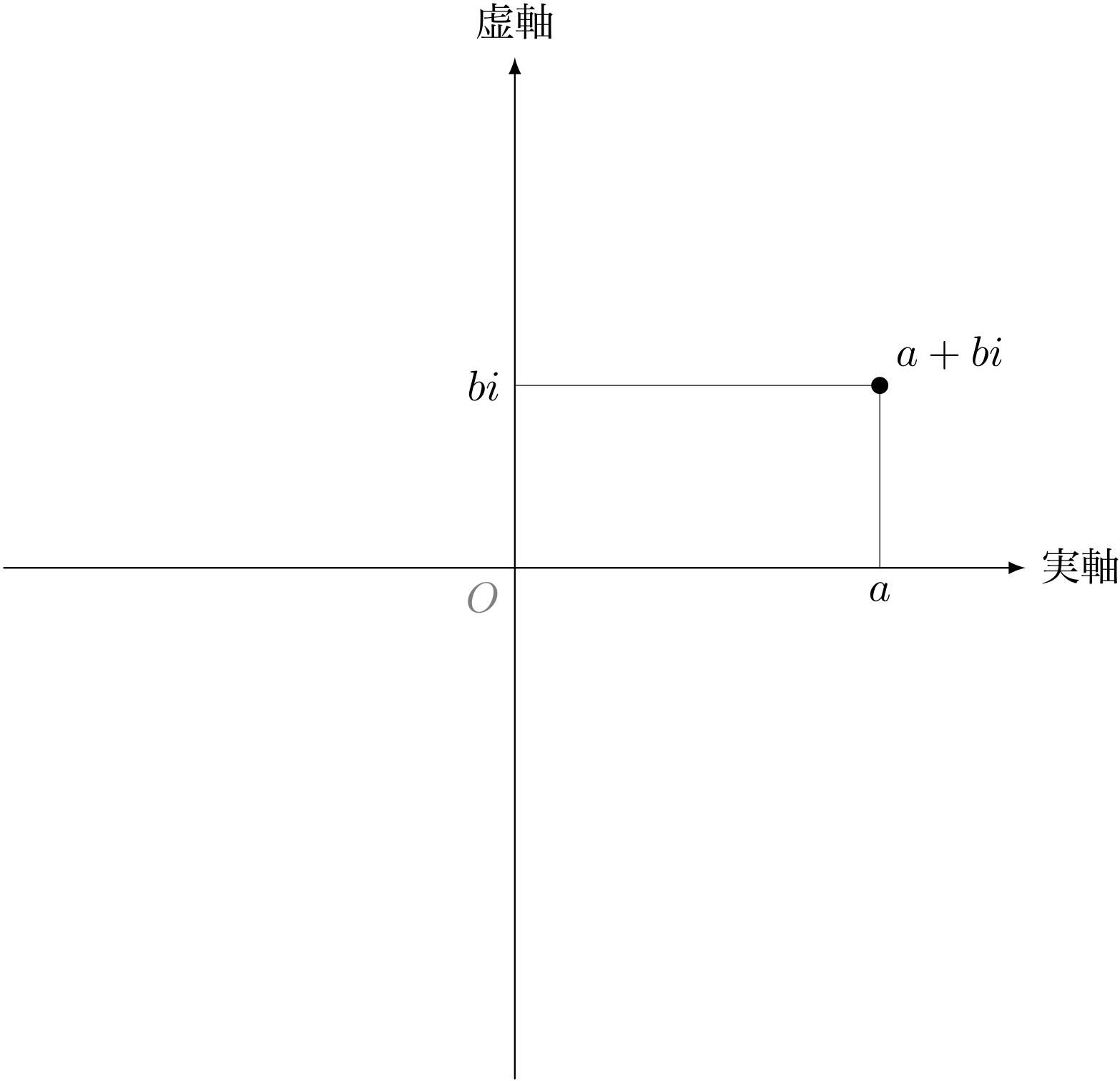
ユーリ「だったらさ、《三次元の数》って作れないの？」

僕「三次元の数？」

ユーリ「うん。複素数を作ったのと同じように、作れないの？」

僕「ええと……ちょっと待った。たとえば複素数 $a+bi$ は点 $(a,b)$ で表すことが できるから、それと同じように考えて $(a,b,c)$ という点を作ることはできるよ。 この場合 $(a,b,c)$ というのは三次元空間上の点になるわけだけど……」

ユーリ「それそれ、そーゆーの。 その《三次元の数》って、高校で習う？」

僕「いや……高校では習わないし、それに、 確か、そんな数は存在しないんじゃなかったかな？」

ユーリ「は？」

僕「うん、何かの本で読んだことがある。 複素数を拡張して新しい数を作るのは、できないはずだよ、確か」

ユーリ「お兄ちゃん、何言ってんの？　そんなわけないじゃん。 だって、いまお兄ちゃん $(a,b,c)$ という点は三次元だって言ったばっかだし。 それに、数学なんだから、何でも定義できるんじゃないの？　新しい数を作るのが《できない》って意味わかんない！」

僕「……うん、もう少し正確にいうと、 実数や複素数が満たすような数の性質を保ったまま、 複素数を拡張して《三次元の数》を作ることはできないはず」

ユーリ「ぜんっぜん、まったく、納得できなーい！　証明してよ」

僕「いやいや、たぶんこれはすごく難しい話になると思うから、僕に証明はできないよ、悪いけど」

ユーリ「……やだ」

僕「ユーリ……」

ユーリ「お兄ちゃん、よく言うじゃん。 自分の《わからない最前線》を見つけなさい、って。先生口調で。 そのお兄ちゃんが、《三次元の数》の証明をやろうともしないで《できない》って言うの？」

僕「わかった、わかったよ。わかりました。じゃあ、できるとこまで、いっしょに考えてみようか。 《三次元の数》が作れないことの証明。 うまく証明できるかもしれないけど、うまくいかないかもしれないよ」

ユーリ「『うまくいくかもしれないし、うまくいかないかもしれない。それは自明である』」

僕「誰の言葉？」

ユーリ「ユーリの言葉」

三次元の数

僕「まずはじっくり始めよう。 証明したいことは何かをはっきりさせないとね。 《証明したいことは何か》」

ユーリ「さっき言ったじゃん」

僕「改めて、きちんと言わないと話は始まらないよ」

ユーリ「うーんとね。 『複素数みたいな《三次元の数》は作れるか？』 を証明したい……これでいい？」

僕「出発点としてはね。 でも、『ナニナニはできるか？』という疑問文は証明の問題じゃないよ。 『できる』か『できない』かを調べることじゃなくて、その理由付けが大事なんだから」

ユーリ「めんどいこと言い出したね？」

僕「証明したいことは『○○である』か『○○ではない』のどちらかの形になる。必ず」

ユーリ「はいはい。だったら、証明したいことは『複素数みたいな《三次元の数》は作れない』だよ。これでいい？」

僕「うん、いいね。それで、次にはっきりさせないといけないのは、 複素数みたいな《三次元の数》っていう言葉の意味だね」

ユーリ「そこはそれ、何となく雰囲気で」

僕「というわけにもいかないよね。 ユーリが好きな《バシッと決める》ためには、 そんなふわふわしたことじゃ証明できない」

ユーリ「けっこう大変なんだ」

僕「……だから、さっきからそう言ってるじゃないか……じゃ、まず、複素数についての復習から行こう。 《はい、これが複素数です》という一番いい方法は、数式を使って書くことだよ。そうすれば誤解がない」

ユーリ「ふむふむ？」

僕「だから、こんなふうに表現する」

ユーリ「$a+bi$ って、よく書くよね、お兄ちゃん」

僕「うん。 $a+bi$ という形に書ける数はすべて複素数で、 逆に複素数ならば $a+bi$ という形で書ける」

ユーリ「いーよ。だったらね……」

僕「ちょっと待って。いま複素数について話したとき、 《実数》と《虚数単位》については何も言わなかったけど、それは大丈夫？」

ユーリ「実数は数直線の数でしょ？　そっか、実数って《一次元の数》なんだ！」

僕「そっちに話が行ったか。そうだよ。その理解でとりあえずはいいんだけど、 言いたかったのは、複素数の定義をするときに、 いちおう実数と虚数単位についてはわかっているものとして定義したよ、 ということ。それを確認したかっただけ」

ユーリ「？」

僕「でないと、いくらでも話をさかのぼらないといけなくなるから」

ユーリ「いーよ。ところでね。《三次元の数》って、ユーリ、わかった気がする！」

僕「へえ？」

ユーリ「《二次元の数》が $a+bi$ なんだから、《三次元の数》は $a+bi+cj$ って書けるものだ！」

僕「なるほど。確かに、そのユーリの考え方は正しそうだね。 というか《三次元の数》というふわっとした言い方をどう定義するかは、 ユーリの自由だからね。でも……」

ユーリ「でも？」

僕「このときにとても大事なのは《その文字は何か》だよ、 ユーリ」

ユーリ「文字って？」

僕「いまユーリは《三次元の数》を、 $$ a+bi+cj $$ と書いたけれど、 ここには $a,b,c,i,j$ という $5$ 個の文字が出てきた。 その $a,b,c,i,j$ という $5$ 個の文字は、それぞれ何を表しているかをはっきりさせようということ。 数式で表すのは大事だけど、 そこに出てくる文字が何かをはっきりさせないと何の意味もないよね」

ユーリ「はいはい、ごもっともですにゃあ。 $a,b,c$ は実数で、 $i$ は虚数単位でしょ。 $j$ は……えっと、なんだろ」

僕「《三次元の数》で新しく登場する、 その $j$ が最重要ポイントだよね。 《三次元の数》を $a+bi+cj$ で表すとして、 $j$ は実数だろうか？」

ユーリ「違うと思う」

僕「違うよね。だって、 $j$ が実数だったら、 $a+bi+cj = (a+cj)+bi$ と書くことができて、 $a+cj$ が実数なんだから、 $(a+cj)+bi$ は複素数の形になってるものね。 《三次元の数》という新しい数にはならなくなっちゃう」

ユーリ「うーん、だったら、 $j$ は複素数でもないよね」

僕「うん、 $j$ は複素数でもない。なぜそういえる？」

ユーリ「さっきのお兄ちゃんの計算と同じ」

僕「そうだね。ちゃんといえば、こうなるよ。 $j$ が複素数なら $j = d + ei$ と書ける。 $d, e$ は実数。 そうすると、《三次元の数》$a+bi+cj$ は、 $$ \begin{align*} a + bi + cj &= a + bi + c(d + ei) \\ &= a + bi + cd + cei \\ &= (a + cd) + (b + ce)i \\ \end{align*} $$ と計算できる。 $a+cd$ と $b+ce$ は実数だから、 $$ (\underbrace{a+cd}_{\REMTEXT{実数}})+(\underbrace{b+ce}_{\REMTEXT{実数}})i $$ という形になっている。つまり、 $(a+cd) + (b + ce)i$ は複素数ということだよね。 そうすると、結局 $a+bi+cj$ は複素数になってしまう。 《三次元の数》という新しい数になれない」

ユーリ「……」

僕「どうした？」

ユーリ「だったら、 $j$ って何？　お兄ちゃんは答えを知ってるの？」

僕「いや、知らないよ。 ユーリは $a+bi+cj$ と書けるものを《三次元の数》と呼べばいいと思った。 僕もそれでいいと思う。では、そのとき $j$ をどう考えればいいのか……それがわかれば、 ユーリのいう《三次元の数》の姿がはっきりするかも。 姿がはっきりすれば、存在しないという証明もできるはず」

ユーリ「へんなの。姿がはっきりすると存在しないってわかるんだ」

僕「そりゃそうだよね。どんなものか定義できなかったら、存在するもしないもないし」

ユーリ「それはいーんだけど！　結局 $j$ って何？」

僕「だから、知らないって。 $a+bi+cj$ の $j$ とは何か。どう考えたらいいのかなあ……」

僕「少し見えてきたよ、ユーリ。しゃべってもいい？」

ユーリ「いーよ」

僕「$j$ というのは $i$ みたいなものだよね」

ユーリ「どゆこと？」

僕「実数 $a,b$ から複素数 $a+bi$ を作るときに虚数単位 $i$ を使った。 それと同じように、複素数 $a+bi$ と実数 $c$ から《三次元の数》$a+bi+cj$ を作るわけだから」

ユーリ「ふんふん」

僕「ということで、もう少し虚数単位 $i$ について考えた方がよさそうだ。 $i$ と $j$ は似ているはずだから。 $i$ についてわかっていることを使って $j$ を考える」

ユーリ「お兄ちゃん、あったまいーね！」

僕「$i$ とは何かというと」

ユーリ「$2$ 乗したら $-1$ だ！」

僕「そうだね。 $i$ は、 $i^2 = -1$ で定義されてる。いいかえると、 $i^2 + 1 = 0$ つまり、 $$ x^2 + 1 = 0 $$ という《$2$ 次方程式の解》であることが虚数単位の本質といえるよね。 この $2$ 次方程式の解は $x = i$ と $x = -i$ の二つあるけれど、 そのうちの片方を虚数単位として使ったわけだ」

ユーリ「わかった！　 $j$ っていうのは $-i$ なんだ！」

僕「残念だけど、そうじゃないよ。さっき考えたように、 $j$ は複素数じゃないんだから……というか、複素数であってほしくないんだからね」

ユーリ「そーだった。それなら、 $j$ って何？」

僕「うん。あのね。さっき浮かんだのはこういうアイディア」

ユーリ「ほほー？」

僕「だからこれを拡張して、 $j$ を決める」

ユーリ「すごーい！　お・も・し・ろ・い！」

僕「それはいいんだけど、係数が複素数になってる方程式か……考えたことなかったなあ……今日は、ここまでかな」

ユーリ「えーっ！」

僕「とりあえず、証明したいことはきちんと書けると思うよ」

ユーリ「$a+bi+cj$ は……何？」

僕「難しいな。《$a+bi+cj$ は新しい数にならない》と言いたいんだけど」

ユーリ「《$a+bi+cj$ は新しい数にならない》じゃだめなの？」