![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/複素数の広がり』として書籍化されています。
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
僕とユーリは、複素平面を使った数学トークを楽しんでいる(第162回参照)。
僕「……複素数 $a + bi$ を、 $(a, b)$ という実数のペアだと見なすのは楽しいんだよ。 $(a,b)$ を座標だと見なすと、平面上の $1$ 点が、複素数 $1$ 個に対応する。 こうやってできた平面には複素平面や複素数平面 という名前が付いている」
複素平面上の点 $(a,b)$ を、複素数 $a+bi$ と見なす

ユーリ「前から気になってたんだけど、 $a + bi$ って数が二つなのに、一つの数なんだね」
僕「そうだね。 《$a,b$ という二つの実数》と考えることもできるし、 《$a+bi$ という一つの複素数》と考えることもできる。 どちらの見方も大事だよ。複素数を一つの文字で表すときもあって、 そのときは、ギリシア文字の $\alpha$ や $\beta$ などを使ったり、 あるいは $z$ を使ったりするよ」
ユーリ「ふーん」
僕「実数は直線上の一点で表されて、複素数は平面上の一点で表される。 平面は横軸と縦軸という二つの直線を組み合わせて作ることができるから、 実数二つの組が複素数一つを表すというのはとても納得がいくよね」
ユーリ「ふんふん」
僕「ユーリは《実数を直線上の点で表す》といわれてすぐわかるの?」
ユーリ「わかるよん。数直線のことでしょ?」
《数直線》
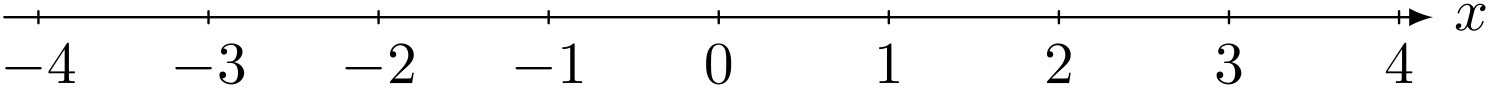
僕「そうそう。じゃあ、実数を数直線で表すと何がうれしいんだと思う?」
ユーリ「は? 別にうれしくない」
僕「え? うーん、じゃあ、うれしくなくてもいいけど、何が便利なんだと思う?」
ユーリ「実数を数直線で表すと便利なこと……ねー、これ、 《みんな仲間でみんな素敵》みたいな答えがユーリに期待されてんの? どんな実数も、 数直線のどこかに収まって《仲良し家族》はいいわねえ、みたいな」
僕「急に斜に構えるなよ。その発想はどこから来るんだ?。 でも《どんな実数も、数直線のどこかに収まる》というのは大事なことだと思うよ。 仲良し家族かどうかは知らないけどね。 $1,2,3,\ldots$ も、 $\frac12, \frac13,\frac14,\ldots$ も、 $\pi$ や $e$ も、一見違うように見えるけれど、ぜんぶ数直線に収まる」
ユーリ「そだね。 $\pi$ は円周率だから $3.14159\cdots$ のあたりにあるわけでしょ。 $e$ って何だっけ」
僕「$e$ は自然対数の底だね。 $e$ は $2.718281828\cdots$ のあたりにある。 $e < \pi$ だよ」
《数直線上の $e$ と $\pi$》

ユーリ「そんで? お兄ちゃんの答えは? 実数を数直線で表すと何がうれしーの?」
僕「もちろん答えは一つじゃないんだけど、お兄ちゃんが考えたのは、 《大小関係がよくわかる》ってことかなあ。 数直線で右に来る実数の方が大きいし、 左に来る実数の方が小さいってわかりやすいよね」
ユーリ「まーね。あたりまえっぽいけど」
僕「それに、数直線があるから、 実数はいかにも《存在する》って感じがする。 右にいくらでも伸ばせるから、いくらでも大きな実数が存在するというのも実感としてよくわかる」
ユーリ「複素数だって存在するじゃん」
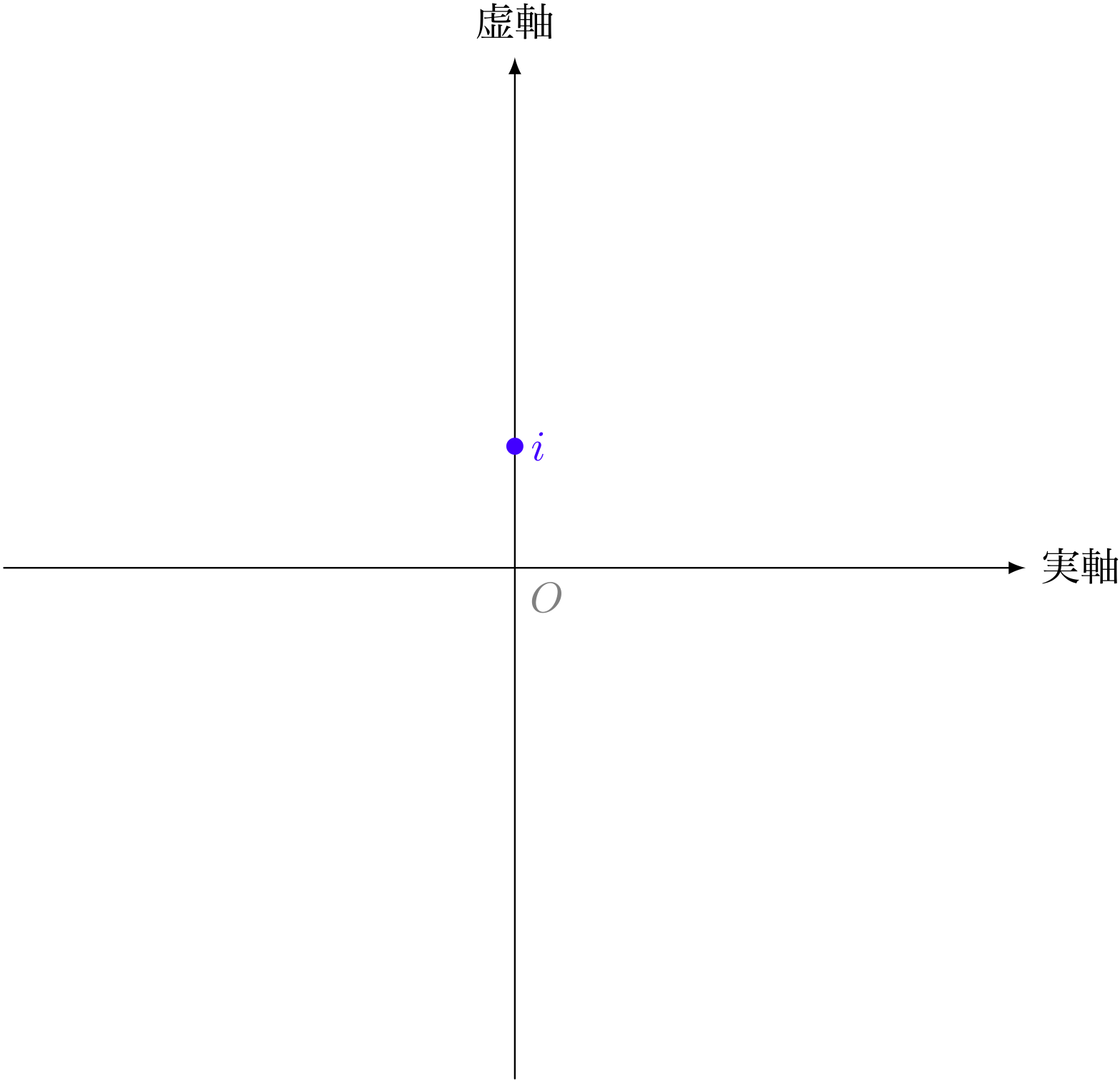
僕「そうだよね! それは複素平面をユーリが見ているからなんだよ、 きっと。虚数単位の $i$ でも、複素平面上で $(0,1)$ の点を指さして、 『ほらここにある』っていえるから、存在するように実感できる」
虚数単位 $i$ は《ここ》にある
ユーリ「あれ? 複素数ってどーなってるんだっけ」
僕「どうなっているとは、何が?」
ユーリ「大きさ。さっきお兄ちゃん『実数は数直線で右にある方が大きい』 って言ったじゃん? 複素数はどーなの? 複素平面で右にある方が大きいの?」
僕「うん。《実数と実数》は大小関係を比べることができるけど、 《虚数と虚数》や《実数と虚数》は大小関係は定義できないんだ」
ユーリ「虚数って何だっけ」
僕「複素数 $a + bi$ で、 $b \neq 0$ のものが虚数だね。 $b = 0$ のものが実数。 複素平面でいえば、実軸以外の点はすべて虚数。 要するに《実数と実数》という実軸の上の数同士でしか大小比較はできないんだ」
ユーリ「なんで? 定義すればいーじゃん。 $i > 0$ とか」
僕「虚数にまで大小関係を入れてしまうと、実数の大小関係と整合性がなくなるんだよ。 たとえば、僕たちが知ってる実数の大小関係には、 $$ a > 0 \,\REMTEXT{かつ}\, b > 0 \Longrightarrow ab > 0 $$ という性質があるけれど、それが成り立たなくなってしまう。 たとえば、 $i > 0$ と決めると、 $$ i > 0 \,\REMTEXT{かつ}\, i > 0 \Longrightarrow ii = i^2 = -1 > 0 \qquad \REMTEXT{(?)} $$ というおかしなことになってしまう」
ユーリ「そんなら、 $i < 0$ と定義したら?」
僕「同じことだよ。 $i < 0$ と定義したら $-i > 0$ にならなくちゃ困る。 そして、 $(-i)(-i) = i^2 = -1$ になるから、やっぱり $-1 > 0$ になってしまうよね」
ユーリ「う……」
僕「だから、虚数が入った大小関係は定義されていない。 でも、複素数の《絶対値》というのが定義されている」
ユーリ「ぜったいち」
僕「複素数 $a + bi$ の絶対値は $\sqrt{a^2 + b^2}$ と定義されているよ」
ユーリ「何でまたそんなややこしー定義を」
僕「いやいや、ぜんぜんややこしくないよ。 複素平面で考えればすごく自然な定義。 だって、複素数 $a + bi$ の絶対値 $\sqrt{a^2 + b^2}$ は、 原点からその複素数までの距離なんだから!」
複素数 $a + bi$ の絶対値 $\ABS{a + bi}$
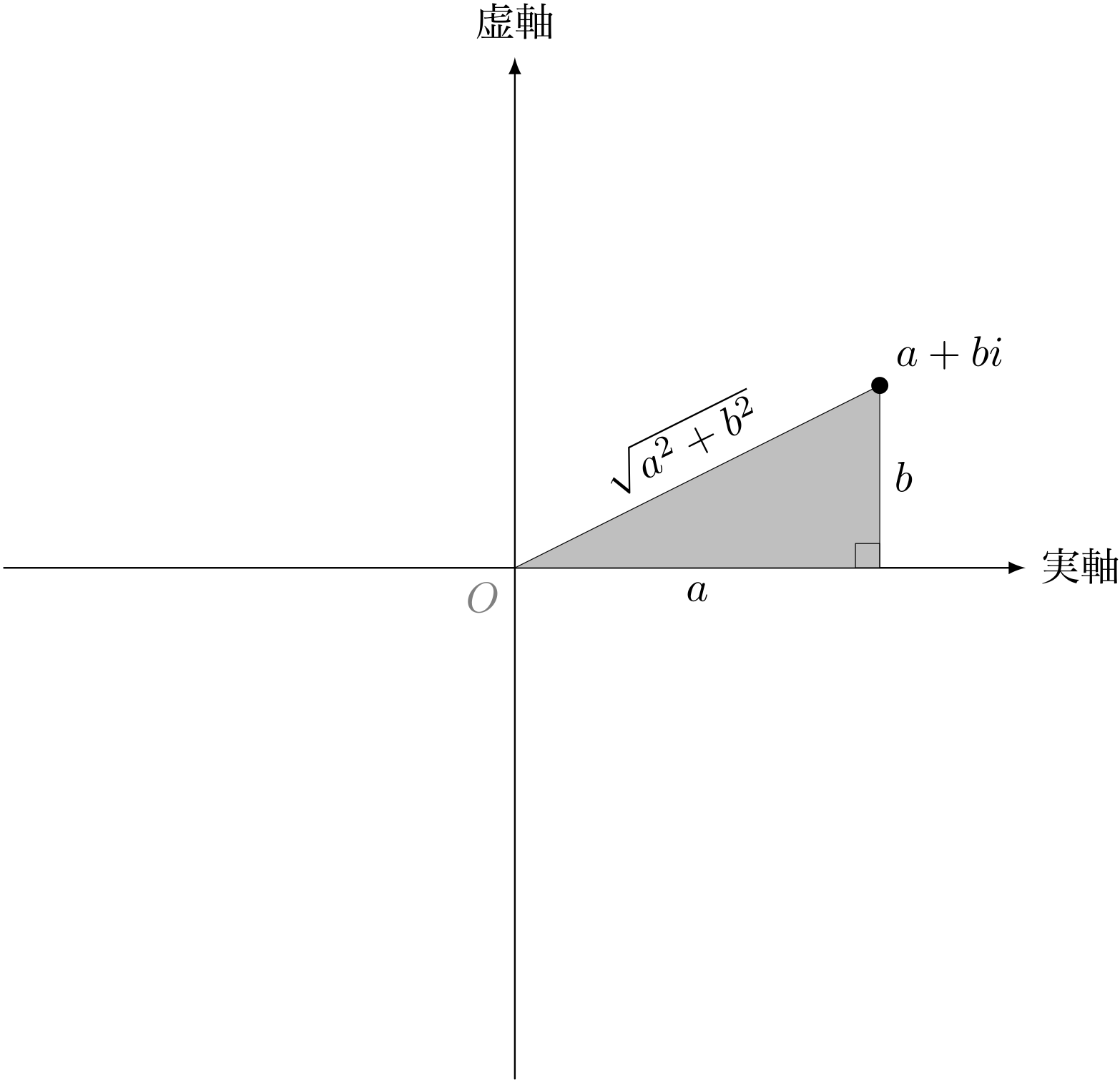
$$ \ABS{a + bi} = \sqrt{a^2 + b^2} $$
ユーリ「ほほー! そっか、直角三角形!」
僕「しかも、この定義は、実数の絶対値の定義とも一致しているんだよ。わかる?」
ユーリ「実数の絶対値って、 $\ABS{-3} = 3$ とかでしょ?」
僕「そうだね。 実数 $a$ というのは、言い換えると $a + 0i$ という複素数だよね。 だから、 $$ \ABS{a + 0i} = \sqrt{a^2 + 0^2} = \sqrt{a^2} = \ABS{a} $$ ということで、つじつまがあってる」
ユーリ「ん? そっか。 $\ABS{-3} = \sqrt{(-3)^2} = \sqrt{9} = 3$ だもんね」
僕「複素平面で、コンパスの針を原点に置き、 もう片方を複素数 $a + bi$ の上に置いたときのコンパスの《開き》が絶対値になってるわけだ。円の半径が $\sqrt{a^2+b^2}$ だね」
コンパスで円を描く
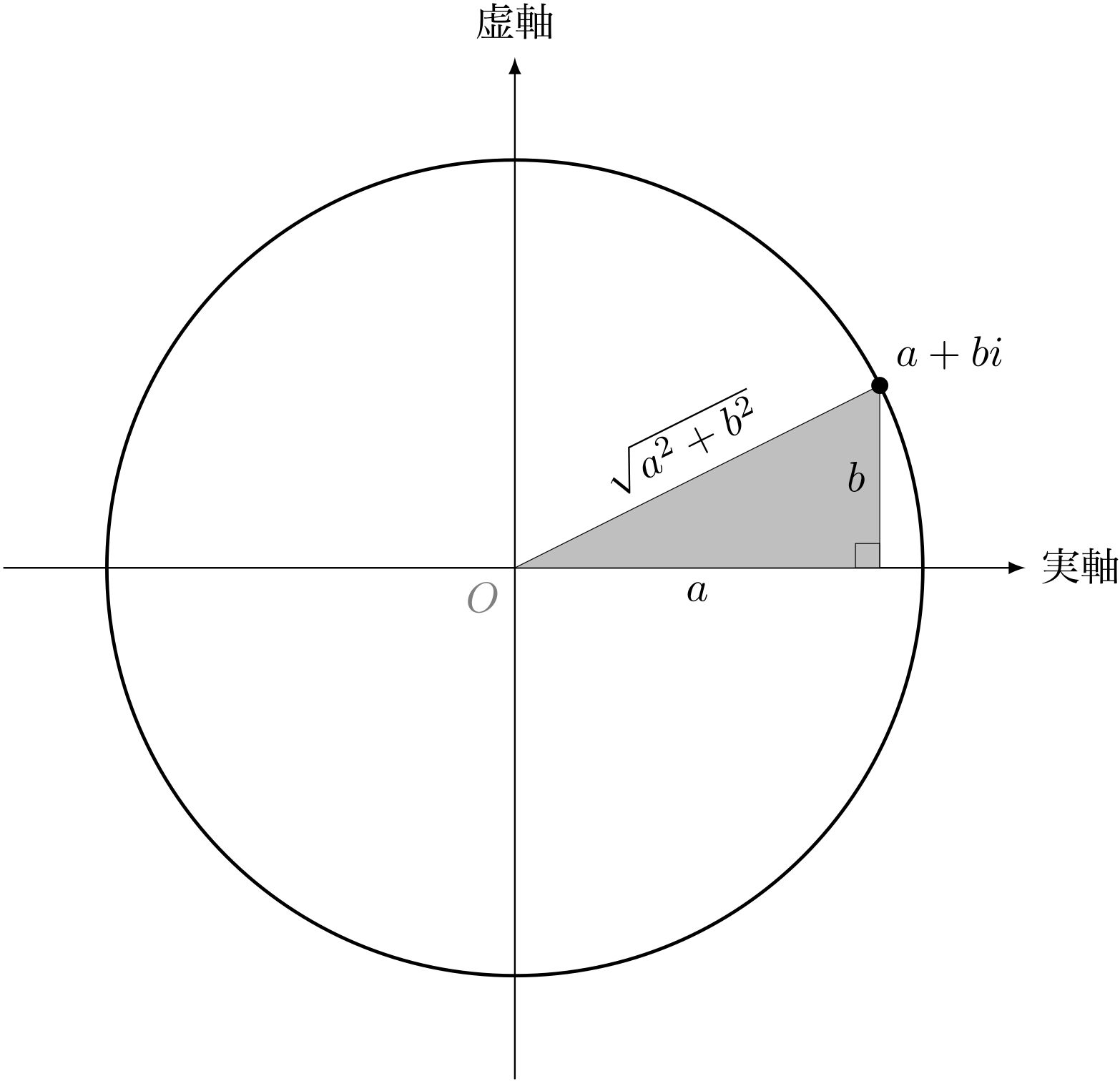
ユーリ「そーだね。あり? とゆーことは、絶対値が同じ複素数ってたくさんある?」
僕「もちろん。このコンパスで描いた円周上にある複素数はすべて同じ絶対値ということになるね」
ユーリ「そかそか! そして、横軸との交点は、絶対値が同じ二つの実数だね!」
僕「その通りだね。実軸との交点は $\sqrt{a^2 + b^2}$ と $-\sqrt{a^2 + b^2}$ という二つの実数」
原点中心、複素数 $a+bi$ を通る円と、実軸との交点
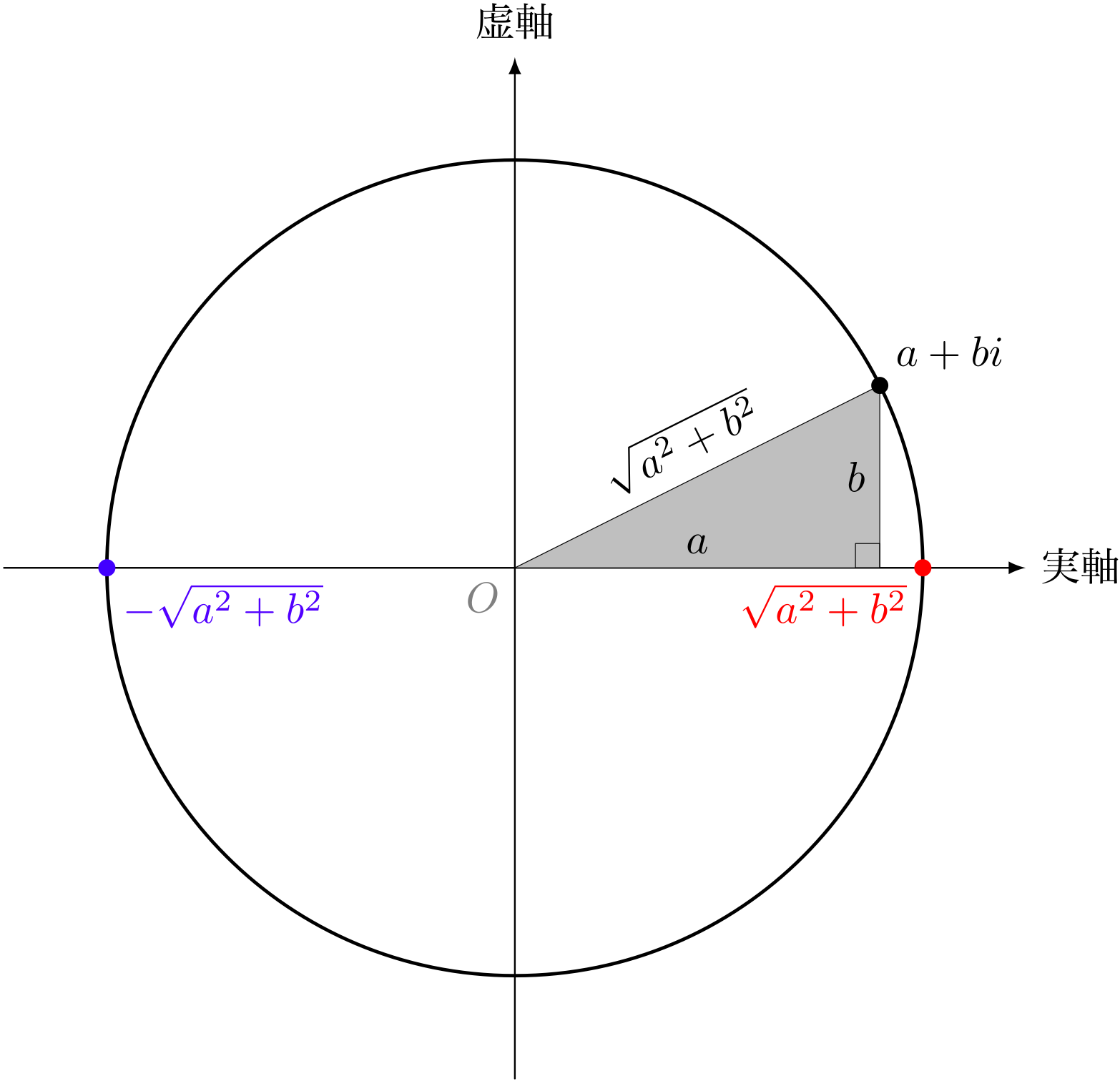
ユーリ「なんか急におもしろくなった。コンパスで直線を切ったみたい」
僕「複素平面を考えると、平面上の《点》がすべて《複素数》に対応しているよね。 てことは《複素数を操作する》というのは《点を操作する》ことを意味する」
ユーリ「意味わかんない。操作するって何?」
僕「ごめんごめん。計算っていったほうがいいかな。 《複素数で計算する》っていうのは、 《点を動かす》ようなものだってこと」
ユーリ「ちゅーしょーてきだにゃあ」
僕「たとえば《$3$ を足す》っていう計算を考えると、 それは《右に $3$ 動かす》っていう操作になるわけだ。 $a+bi$ という複素数に $3$ を加えて $(a+3)+bi$ になるから、 $$ a+bi \stackrel{+3}{\longmapsto} (a+3) + bi $$ という計算と、 $$ (a,b) \stackrel{\REMTEXT{右に$3$動かす}}{\longmapsto} (a+3,b) $$ という点の移動が対応する」
《$3$ を足す》と《右に $3$ 動かす》

ユーリ「にゃるほど。んじゃ《$3$ を引く》ってゆーのは、《左に $3$ 動かす》こと?」
僕「そうなるね。それじゃクイズ。《$i$ を足す》 という計算は、どういう移動になる?」

ユーリ「そんなのカンタン! 《$i$ 足す》のは《上に $1$ 動かす》でしょ?」
$$ \begin{align*} a+bi & \stackrel{+i}{\longmapsto} a + (b+1)i \\ (a,b) & \stackrel{\REMTEXT{上に$1$動かす}}{\longmapsto} (a,b+1) \end{align*} $$《$i$ 足す》と《上に $1$ 動かす》

僕「そうだね。そして《$3 + i$ を足す》のは《右に $3$ 動かし、上に $1$ 動かす》ことに相当するわけだ。 言い換えると《複素数を足す》というのは《平行移動》になっているんだね」
《$3 + i$ を足す》と《右に $3$ 動かし、上に $1$ 動かす》
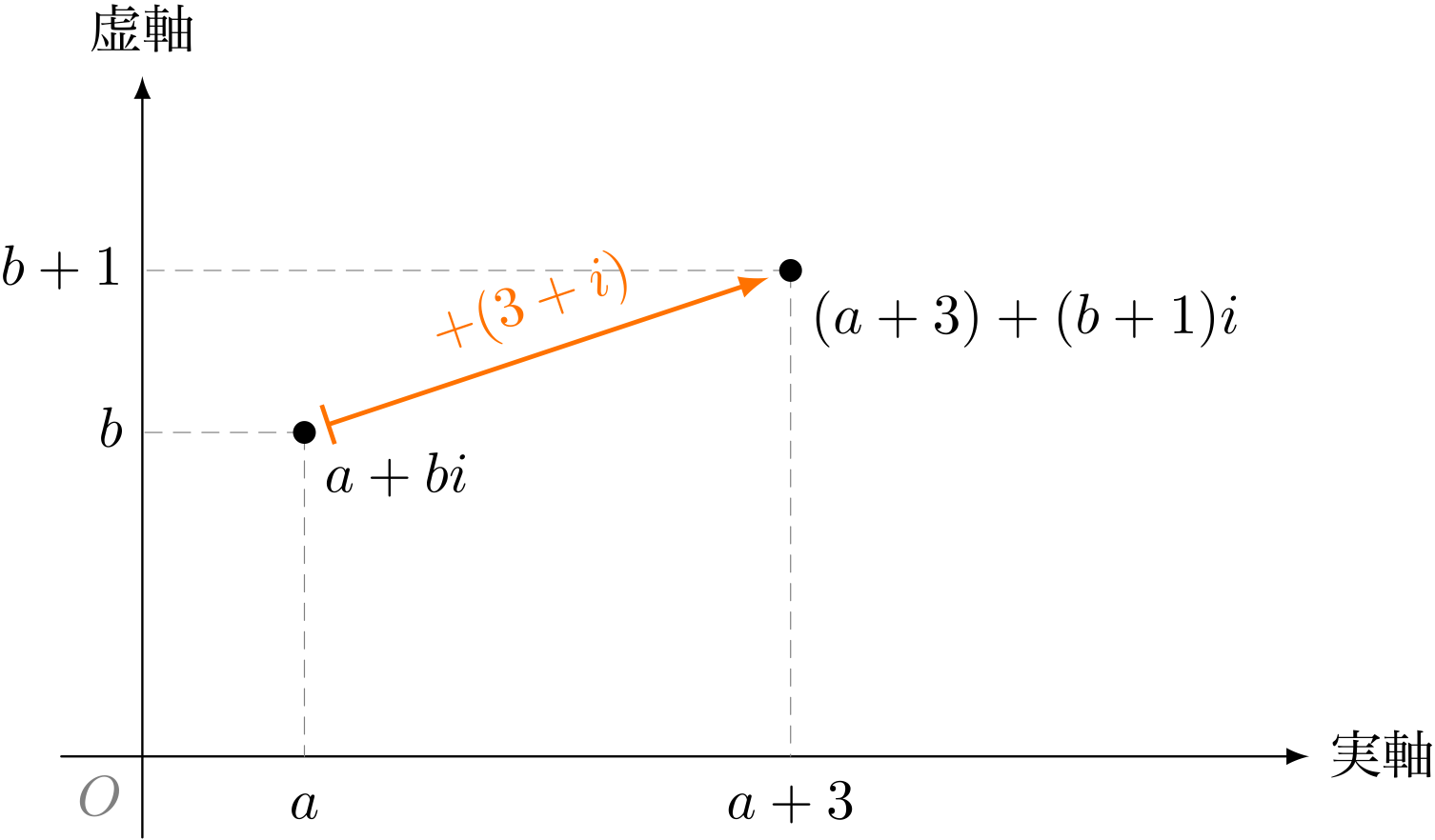
ユーリ「にゃるほど……あれ、お兄ちゃん? これってもしかしてベクトルで似たよーなことやらなかった?」
僕「ああ、そうだね。二つの平面ベクトルを足し合わせるところだね」
ユーリ「そーそー! あんときは平行四辺形が出てきてた。二つのベクトルを足すと、その対角線」
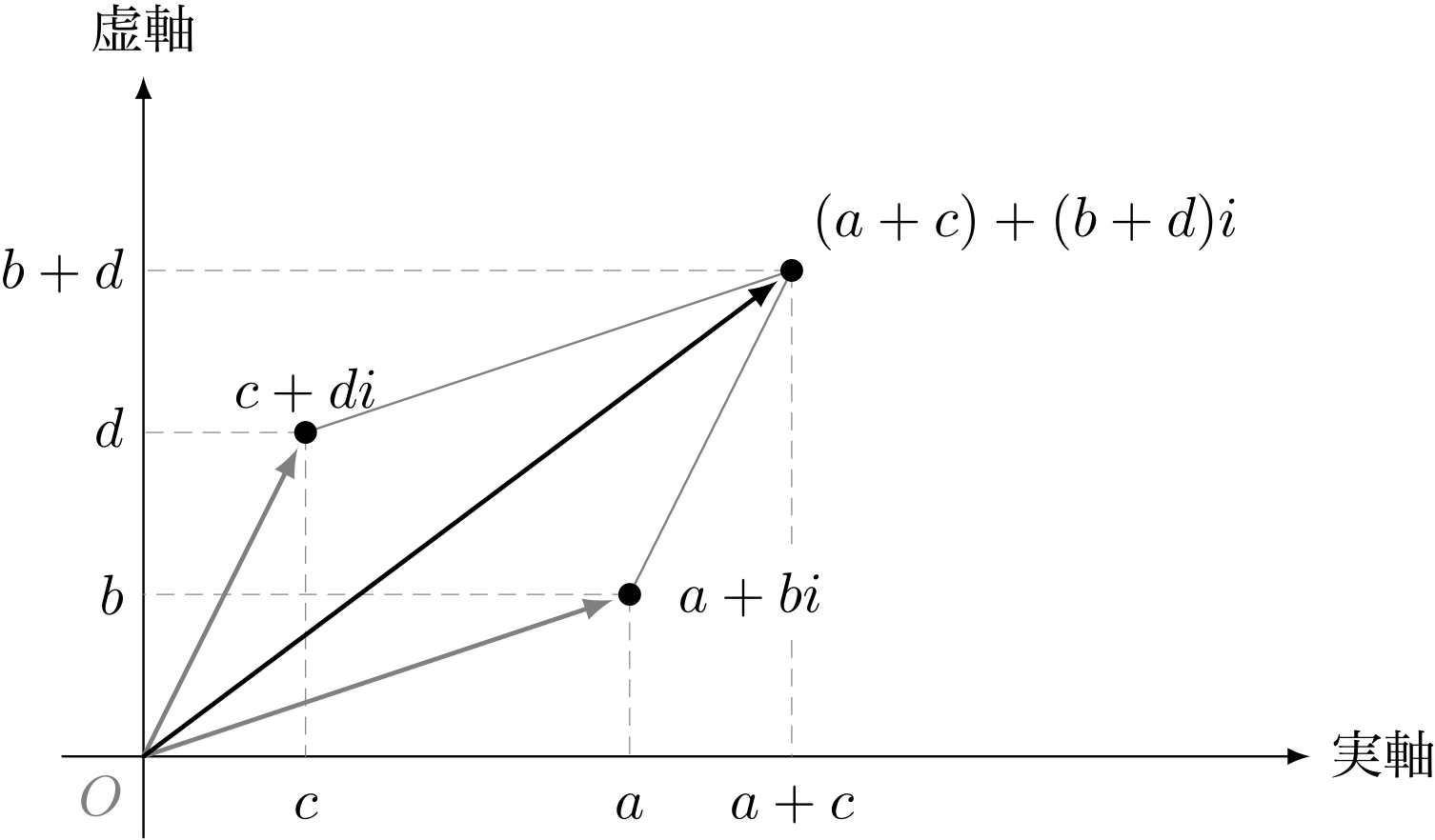
僕「うん。二つのベクトル $(a,b)$ と $(c,d)$ を加えると $(a+c, b+d)$ になる。 図形で表すと、二つのベクトルと原点をそれぞれ結んだ線分を二辺にする平行四辺形の対角線になる。 これは全部、同じものを見ているんだね」
複素数の和
$$ (a + bi) + (c + di) = (a+c) + (b+d)i $$

ベクトルの和
$$ (a,b) + (c,d) = (a+c, b+d) $$

ユーリ「おんなじだね」
僕「そういえば、ベクトルの大きさの定義も、複素数の絶対値と同じだよ」
ユーリ「ふんふん。いろんなのが関係してるんだ」
僕「そうだね。こんなふうに複素平面を考えると、 計算と図形が関係していることがよくわかる」
ユーリ「……あれ? ちょっと待って、なんか変だ」
僕「何が変?」
ユーリ「図で引っかかりそうになったけど、 さっきの、平行四辺形じゃないよね」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2016年7月22日)
この記事は『数学ガールの秘密ノート/複素数の広がり』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!