![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/数を作ろう』として書籍化されています。
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。好奇心旺盛で根気強い《元気少女》。
ミルカさん:数学が好きな高校生。僕のクラスメート。長い黒髪の《饒舌才媛》。
いまは放課後。ここは高校。僕がいつものように図書室に行くと、 テトラちゃんがノートを見つめていた。
僕「テトラちゃん、今日も熱心だね」
テトラ「あっ、先輩! いえ、あの、 やっぱりあたしは、どうも考える力が低いようです」
僕「そんなことないよ! テトラちゃんはいつもしっかり考えるじゃないか。 誰よりも粘り強いし、それになかなか納得しない」
テトラ「ありがとうございます。でも、あたしが納得しないのは、 頭が問題についていけてないからで……」
僕「どんな問題を解いているの?」
テトラ「いえいえ、何か問題を解いているわけではなくてですね、 ミルカさんのお話を思い出して、《もやもや》しているだけで……」
僕「まあ、ミルカさんは難しい話もぽんぽんと出してくるから」
テトラ「そうなんですが、あたしが気になるのは、 本来ならあたしが《わかるべき話》なんじゃないか、と思うときなんです」
僕「どういうこと?」
テトラ「つまりですね。お話ししている内容がとっても難しくて高度なときには、 『うわわわ』とは思いますが、『もやもや』とは思いません。 でも、とても簡単そうに見えるけれど、あたしにはよくわからないとき、 そんなときに《もやもや》するんです」
僕「いまのテトラちゃんの話で、僕が《もやもや》しているけど……具体的には、 ミルカさんのどんな話のことだろう」
テトラ「あっ、そうですよね。 あたしが気になっているのは、《デデキントの切断》の話です」
僕「ああ、そんなおしゃべりしたよね(第156回参照)」
《集合を切断する》
要素に大小の順序が定められている集合 $X$ に対して、 以下の性質すべてを満たす集合 $A,B$ を考える。
(1)$A$ も $B$ も空集合ではない。 $$ A \neq \{\}, B \neq \{\} $$
(2)共通部分は空集合。 $$ A \cap B = \{ \} $$
(3)和集合は $X$ 全体。
$$ A \cup B = X $$
(4)$A$ の任意の要素 $a$ と、 $B$ の任意の要素 $b$ に対して、 $$ a < b $$ が成り立つ。
このとき、順序対 $(A,B)$ を $X$ の切断と呼ぶ。
テトラ「はい……そして《有理数全体の集合》の切断 $(A,B)$ を考えて、 その切断一つを《実数》とみなすことができる。そういうお話でした」
僕「そうだね。ええと、そうそう、集合 $A$ の最大値 $\max A$ と、集合 $B$ の最小値 $\min B$ が存在するかどうかを考えたんだった」
テトラ「そうです。あたしはノートに整理しました」
(ケース1)$\max A$ は存在する。 $\min B$ も存在する。
→ これは、ありえません。有理数全体の集合は稠密だからです。
(ケース2)$\max A$ は存在する。 $\min B$ は存在しない。
→ これは、有理数になります。 $\max A$ がその値です。
(ケース3)$\max A$ は存在しない。 $\min B$ は存在する。
→ これも、有理数になります。 $\min B$ がその値です。
(ケース4)$\max A$ は存在しない。 $\min B$ も存在しない。
→ これを、無理数とみなします! 白丸と白丸の切断、その境目です!!!!
僕「テトラちゃんの《秘密ノート》登場だね。白丸と白丸……?」
テトラ「あたしのイメージはこうなんです」
《有理数全体の集合》を切断する
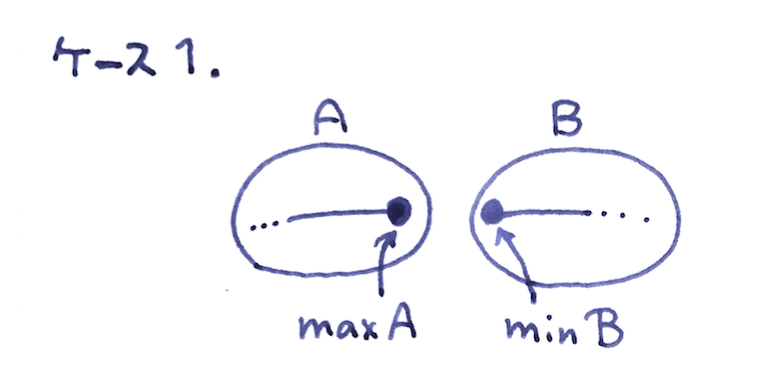

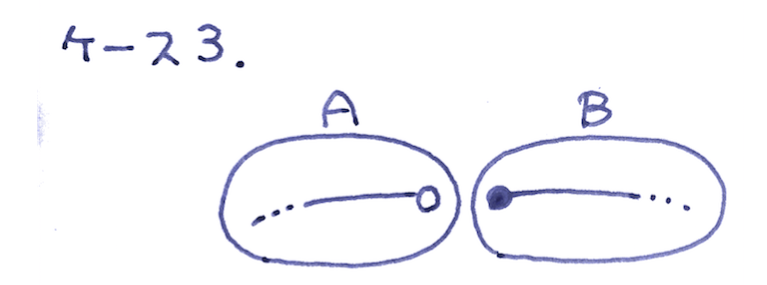

僕「なるほど、なるほど。確かに白丸だね。 なんだ、テトラちゃんはすごくよくわかっているよ。僕よりもちゃんと整理してわかっている」
テトラ「ちがうんです。問題はここからです。あたしはこの(ケース4)で『はてな?』と思いました」
僕「……」
どうしてテトラちゃんは『はてな?』というときに、 実際に首を傾げる仕草をするんだろう。
テトラ「たとえば、 $(A,B)$ という切断で $\sqrt{2}$ という無理数を表せるというんですよね?」
僕「そうだよ。《$\sqrt{2}$ よりも小さな有理数全体の集合》を $A$ として、 《$\sqrt{2}$ よりも大きな有理数全体の集合》を $B$ とすればいいよね。 そうすれば、僕たちの手元には有理数しかないのに、 $(A,B)$ は $\sqrt{2}$ という無理数を指し示していることになる。おもしろいよねえ」
テトラ「ほんとうにそうなんでしょうか?」
僕「というと?」
テトラ「いま、あたしたちは有理数しか知らないんですよね。 それなのに、《$\sqrt{2}$ よりも小さな有理数全体の集合》を $A$ として、 《$\sqrt{2}$ よりも大きな有理数全体の集合》を $B$ とすればいい……というのは、 おかしいんじゃないでしょうか。だって、知らないはずの無理数の $\sqrt{2}$ を持ち出してきています!」
僕「ああ、それは言葉の綾というか、話を先取りしているだけで、 実際には《$\sqrt{2}$ よりも小さな有理数全体の集合》を $A$ とするわけじゃなくて、 《有理数を $2$ 乗したときの値》を使うんだよ。そうすれば $\sqrt{2}$ という無理数は表には出てこない」
テトラ「あ! 確かに、そうすればいいですね! ということは、 $A$ は、 《$2$ 乗したら $2$ よりも小さくなる有理数全体の集合》と定義すればいいんですね!」
僕「惜しいけど、条件が抜けているよ、テトラちゃん。 負の数のことを忘れている。 $A$ は、《$0$ よりも小さいか、 $2$ 乗したら $2$ よりも小さくなる有理数全体の集合》だね」
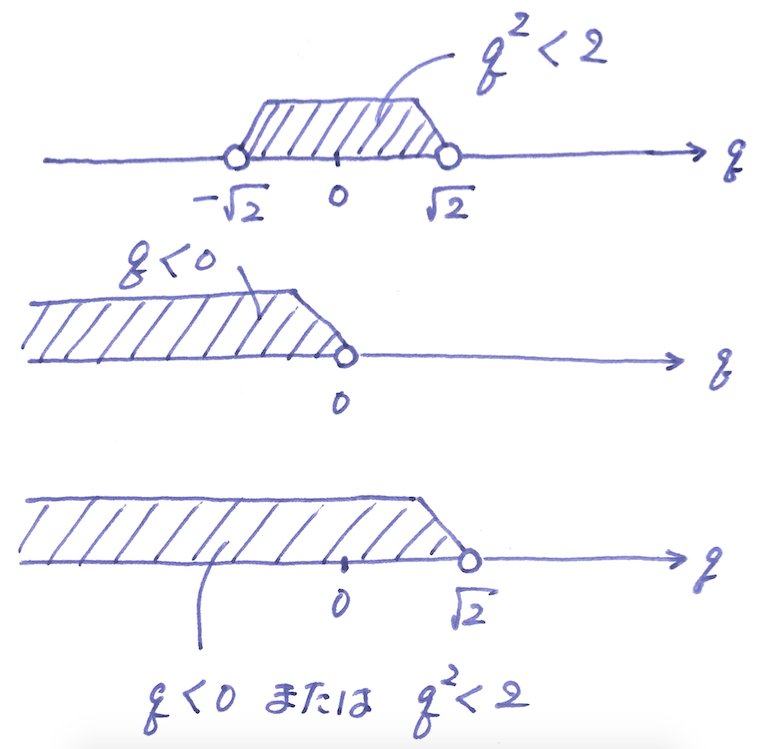
テトラ「あちゃあ……そうですね。 と、ともかく、そこまでは理解しました。 $\sqrt{2}$ という無理数を持ち出さなくても大丈夫と」
僕「うん。それに、実数は $\sqrt{2}$ のように、方程式の解として得られる数とは限らないから、 $1.41421356\cdots$ のように無限に続く数字列で考えた方がいいかもしれないけどね。 これで、テトラちゃんの《もやもや》は解決したの?」
テトラ「はい! 一つ目の《もやもや》については!」
僕「おっと、まだあるんだ」
テトラ「《有理数全体の集合》を切断して実数を作るというお話の中で、 $\max A$ と $\min B$ のどちらも存在しないときが無理数に対応していましたよね」
僕「そうだね。テトラちゃんのノートでは(ケース4)と書いていた」

テトラ「でも、ほんとうにこれで実数が決まるんでしょうか」
僕「うん、決まると思うけど。テトラちゃんは何を気にしているの?」
テトラ「あたしが気にしているのは……あのですね、 (ケース4)の切断で決まる無理数が《唯一》である保証はどこにあるのかということです」
僕「おお!」
テトラ「はい。(ケース4)の切断で有理数以外の何かを決められるのはわかります。 少なくとも有理数は決めていません。 でも、それを無理数としたとしても、その数が《たった一つ》に決まるとどうしていえるんでしょうか。 もしかしたら、 $(A,B)$ というひとつの切断で、二つの無理数が決まるかもしれませんよね? そこが《もやもや》しているんです!」
僕「なるほど……」

テトラ「でも、先輩! 不思議です。 先輩にこうやってお話ししていると、それだけで何だか心が整理されていくようです。 ひとりでずっと考えているのとは違いますね」
僕「人に話すと整理されるからね……ところで、 テトラちゃんのその疑問については、以前議論しなかったっけ。 ほらテトラちゃんが(ケース4)がありうるかどうかを気にして」
テトラ「それは、(ケース4)がありうるかどうかの話だったと思います。 もう(ケース4)がありうるのはわかります。 あたしが悩んでいるのは、(ケース4)の切断 $(A,B)$ で、 $A$ と $B$ の間に入る無理数が《複数個》存在することはありえないのか、ということなんですが」
僕「そうか……いやいやわかったぞ! それは簡単な話だよ。 複数個存在することは《ない》ね。証明もできるよ」
テトラ「そうなんですか!」
僕「$A$ と $B$ の間に入る二つの無理数があったとする。 ちゃんというと、 $$ \max A < a < b < \min B $$ という無理数 $a,b$ が存在したと仮定する。そういうことだよね?」
テトラ「そうです、そうです! 切断 $(A,B)$ で、 $A$ と $B$ の間には複数の無理数があってもおかしくないです! $2$ 個の無理数といわず、 無数の無理数があいだに入るかも知れませんし!」
僕「$a$ と $b$ を具体的に書くと、たとえば、こんなふうになるはずだよね。 $\clubsuit$ と $\diamondsuit$ は《どこか》が違う数字列として」
$$ \left\{\begin{array}{llll} a &= 1.41421356\underbrace{\cdots}_{\clubsuit} \\ b &= 1.41421356\underbrace{\cdots}_{\diamondsuit} \\ \end{array}\right. $$テトラ「……はい、そうです。 $a < b$ ということは、 $a \neq b$ ですから、 $a$ と $b$ の数字はどこかで違っています」
僕「テトラちゃん、そこだよ。いまテトラちゃんが言ったことに証明のカギがある。 無理数 $a$ と $b$ を書き表したとき、どこかの桁で初めて数字が違うなら、その桁に注目すればいい。こんなふうに」
$$ \left\{\begin{array}{llll} a &= \underbrace{1.41421356\cdots}_{\heartsuit}4\cdots \\ b &= \underbrace{1.41421356\cdots}_{\heartsuit}5\cdots \\ \end{array}\right. $$僕「いまは仮に $a$ は $4$ で、 $b$ は $5$ としたけど、なんでもいいよ」
テトラ「この $\heartsuit$ の部分はすべて同じ数字列ということですね……だめです。 やっぱり、あたし、考える力、弱いです。やっぱり $a$ と $b$ 以外にも無数の無理数があるとしか思えません」
僕「《求めるものは何か》だよ。僕たちはいま、何を求めているんだろう」
テトラ「無数の無理数……」
僕「じゃないよ。僕たちは、 $\max A < a < b < \min B$ という $2$ 個の無理数が存在するという仮定からスタートした。 僕たちは《背理法》で証明しようとしているんだよ?」
テトラ「あっ、矛盾です! あたしたちは矛盾を求めているんです! ……でも、やっぱりわかりません」
僕「《与えられているものは何か》はどうだろう」
テトラ「あたしたちに与えられているもの……それは切断 $(A,B)$ です。《有理数全体の集合》を $A,B$ に分けました」
僕「ということは、 $a$ と $b$ のあいだに有理数は存在しないはずだよね?」
テトラ「それはそうです。モーセが海を分けたように、有理数は左右にわかれて……わかれて……わかりました! さっきの《数字が変わる桁》ですね!」
僕「そうそう」
テトラ「$b$ の《しっぽ》を切ってしまえば、有理数 $c$ が作れます! すると $a < c < b$ になりますから、 $c$ は $A$ にも $B$ にも属しませんね……有理数なのに!」
$$ \left\{\begin{array}{llll} a &= \underbrace{1.41421356\cdots}_{\heartsuit}4\cdots && \REMTEXT{無理数} \\ c &= \underbrace{1.41421356\cdots}_{\heartsuit}5 && \REMTEXT{有理数を作った} \\ b &= \underbrace{1.41421356\cdots}_{\heartsuit}5\cdots && \REMTEXT{無理数} \\ \end{array}\right. $$僕「そうだね。いまは $4$ や $5$ という具体的な数でやっちゃったけれど、それで証明はおわりになるよ」
テトラ「なるほどです! こういうことですね」
僕「そうだね。これでテトラちゃんの《もやもや》は解決……どうしたの?」
テトラ「情けないです……。こんなに簡単なことなのに、どうして自力で解決できないんでしょう。 切断、有理数、無理数、背理法、あたしはわかっていたつもりなのに。 先輩の答えを聞いたあとは、もう『あたりまえ』としか思えないのに、 どうして、あたしは、答えを聞くまでわからないんでしょう」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2016年6月3日)
この記事は『数学ガールの秘密ノート/数を作ろう』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!