![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/やさしい統計』として書籍化されています。
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだけれど飽きっぽい。
僕とユーリはリビングでテレビを見ていた。
僕「ほらほら、またこれだよ」
ユーリ「何が?」
僕「いまのニュースに出ていたじゃないか」
ユーリ「え? 何が出たっけ」
僕「グラフだよ。よく出るんだよ」
ユーリ「意味わかんない。そりゃグラフが出るときもあるよね。 さっきは何だっけ。よく見てなかったけど……折れ線グラフ?」
僕「そうだね。ねえ、ユーリはグラフのこと《わかりやすい》と思う?」
ユーリ「来たな。お兄ちゃんの《先生トーク》。その手には引っかからないよーだ!」
僕「先生トークなんてしてないよ」
ユーリ「してたしてた。『グラフのこと《わかりやすい》と思う?』なーんて、当たり前の質問するじゃん? そこに引っかかって、 『そーだね! わかりやすいと思うよ』って答えるじゃん? そしたらお兄ちゃんは『そう思うよね、でも違うんだ』と上から目線で言う。 なんとゆーお決まりの流れ。これを《先生トーク》と言わずになんと呼ぶ」
僕「いきなり饒舌になったな」
ユーリ「そろそろ《饒舌才媛》の二つ名も、ユーリのものかにゃ?」
僕「それはさておき、グラフのこと《わかりやすい》と思う?」
ユーリ「……そりゃー、わかりやすいんじゃない? だってさ、数字がばらばら並んだ表を見せられてもよくわかんないもん。 グラフのほうがずっとわかりやすい」
僕「そう思うよね。でも違うんだ」
ユーリ「……」
僕「世の中の多くの人が、グラフのことをわかりやすいと思う。 確かに、表を見るよりもグラフのほうがパッとみてわかる……ように感じる」
ユーリ「でも違う?」
僕「うん。パッとみてわかるのはいいんだけど、問題は《グラフを見たときに、ほんとうに正しくわかるか》なんだよ」
ユーリ「えー、見てわかるなら、そりゃ、正しくわかるんじゃない?」
僕「具体的なグラフを作ってみよう。ちょっとテレビ切って」
ユーリ「へーい」
僕「これから話すのは架空のデータだよ。たとえば……そうだなあ、ある会社の社員数を調べるとする」
ユーリ「ふんふん? たとえば『ユーリ法律事務所』とか」
僕「法律事務所? まあ、何でもいいんだけどね。ユーリが社長なのかな」
ユーリ「ふふ」
僕「ともかく、その会社の社員数を考える。初めの年、つまり $0$ 年目は社員が $100$ 人で、 $1$ 年目は $117$ 人とするよ。たとえば」
ユーリ「$1$ 年目、社員が増えたんだ」
僕「そうそう。さらに、毎年調べると、 $126$ 人、 $133$ 人、 $135$ 人、 $136$ 人と変化していった……としよう」
ユーリ「いやー、そんなにペラペラ数字を言われましても」
僕「うん、だから、こういうときには表を作るといいよね。 表を使えば、毎年の社員数がはっきりとわかる」
ユーリ「そだね」
社員数の表を作る
$$ \begin{array}{c|cccccccc} \REMTEXT{年数} & 0 & 1 & 2 & 3 & 4 & 5 \\ \hline \REMTEXT{人} & 100 & 117 & 126 & 133 & 135 & 136 \\ \end{array} $$
僕「これを見ると……何がわかる?」
ユーリ「社員数がわかる」
僕「そうなんだけど、ほかにどんなことがいえる?」
ユーリ「増えてる」
僕「うん、社員数が増えていることがわかるね。数字を順番に見ていくとだんだん増えているから」
ユーリ「簡単じゃん」
僕「この会社の社長が……ユーリ社長が、表をもとにして、社員数の変化のようすを調べようと思った。 その場合は、たとえば、折れ線グラフを描いてみることになる。 棒グラフでもいいけど」
ユーリ「うん」
僕「折れ線グラフを作るのは難しくないよね。こんな感じになる」
社員数の折れ線グラフ
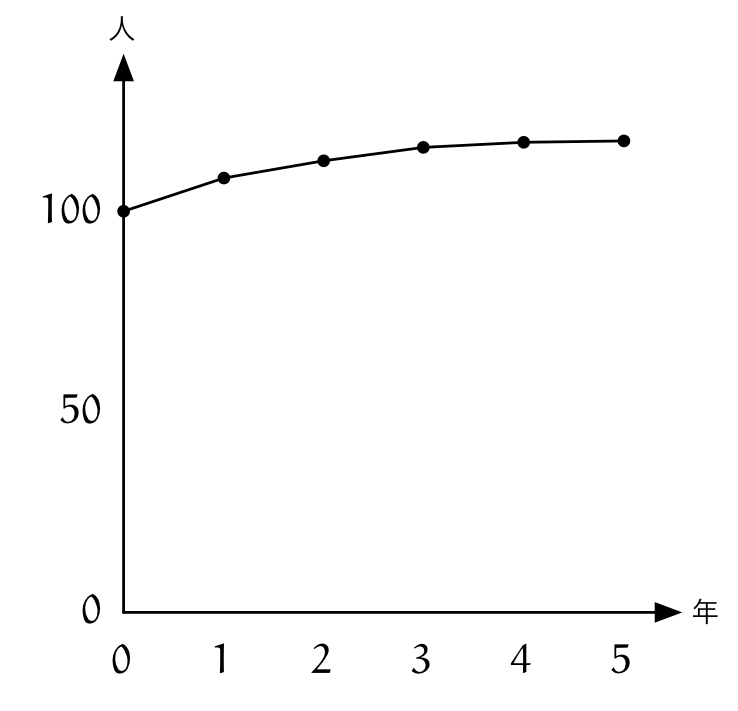
ユーリ「うん、問題ないよ。やっぱり社員数は増えてるね。まー少しずつだけど」
僕「でも、ユーリ社長はこれが気にくわない」
ユーリ「は?」
僕「ユーリ法律事務所を経営している社長のユーリは、社員数の増加が少しずつなのが気にくわないとする」
ユーリ「じゃ、たくさん雇えばいいじゃん」
僕「なかなかそうもいかない。だから、こんなことを考えた。『グラフを修正して、社員数の増加が大きいように見せてやろう!』」
ユーリ「データのカイザンだ!」
僕「いやいや、データを改竄するわけじゃない。正義感あふれるユーリ社長は、そんなことしないよね?」
ユーリ「もちろんじゃ」
僕「グラフの下をちょっと切り取るだけだよ。こんなふうに」
下を切り取った折れ線グラフ

ユーリ「ほほー。確かに、社員がぐっと増えたように見える……かな」
僕「グラフを見るときに大事なことは何だか知ってる?」
ユーリ「大事なこと……軸を見るだっけ」
僕「そうだね! グラフを見るときには必ず軸と目盛りをチェックするんだよ」
ユーリ「はいはい、センセー」
僕「下を切り取ったグラフの縦軸をよく見ると、『ここを省略してますよ』という波線が入っているよね、ほら」

ユーリ「あるねー」
僕「だから、データの改竄をしているわけでもないし、折れ線グラフに何かウソがあるわけでもない。 つまりこれは《正しいグラフ》だよね」
ユーリ「うん、正しーっちゃ正しーけど……」
僕「でも、ユーリ社長はこれでも気にくわない」
ユーリ「は?」
僕「グラフの下を切り取っただけだと、社員数の増加はそれほど大きく見えない」
ユーリ「だって、データは同じなんだもん」
僕「そこで、こんなふうにグラフを縦に引き延ばしてみた」
切り取ってさらに引き延ばした折れ線グラフ

ユーリ「何これすごい! ってか、何これひどい! 社員数がめちゃめちゃ増えてるみたいじゃん!」
僕「でも、グラフでウソをついているわけじゃない。グラフの縦軸の目盛りをよく見ると、 さっきの《下を切り取った折れ線グラフ》よりも間隔が大きくなっているから、 グラフが表している数値そのものを改竄しているわけじゃない。 だから、これも《正しいグラフ》といえる」
ユーリ「……ねー、お兄ちゃん。確かにそーかもしんないけど、 ユーリは正しくないと思っちゃう。だって、社員数の増加が実際よりも大きく見えるもん」
僕「そうだね。そこは大事なところ。そして微妙なところでもある。 繰り返しになるけれど……下を切り取っても、 さらに引き延ばしても、表している数値をごまかしているわけじゃないから、 あくまでこれは正しいグラフといえるんだよ。 ただし、そこにグラフを作る人の意図が入り込んでいることは確かだね」
ユーリ「意図?」
僕「そう。グラフを使って社員数の増加を大きく見せたい、という意図だね」
ユーリ「そんなのまちがっている!」
僕「ところが必ずしもそうじゃない。さっきのように切り取って引き延ばすと、 細かい変化の様子が拡大されてよくわかるようになる。 つまり、場合によってはデータのようすをはっきりと見せることになるんだ。 切り取ったから悪い! 引き延ばしたからまちがっている! のようにいちがいに決めつけることはできないんだよ」
ユーリ「そーかなー」
僕「だから、グラフを見る側のほうで注意深く読み取る必要がある」
ユーリ「どゆこと?」
僕「ここまでの話は《グラフを見せる側》の話だった。 グラフを見せる側が切り取って拡大して『ほらすごいだろ』といってきたときには、 《グラフを見る側》が『もしも下を切り取らなかったら、どんな印象を与えるグラフになるんだろう』と考えればいい。 そして、自分でグラフを作り直してみる。 そうすれば、ユーリ社長がいくら『社員数はこんなにすごく増加している!』とグラフで主張しても、 反論するグラフを作ることができるわけだね」
ユーリ「にゃるほど……」
僕「ところでここに、ユーリ社長に反旗を翻す専務が登場する」
ユーリ「は?」
僕「専務だよ。専務は次期社長の座を狙っていて、社長の主張に反対したい……としよう。 つまり『実のところ、社員数はそれほど増加していない』という印象を、グラフを使って他の人に与えたいとする」
ユーリ「陰謀渦巻く会社だにゃ」
僕「そこで、こんな表を作った。社員数の《前年からの増加分》を考えることにしたんだ」
前年からの増加分を表にした
$$ \begin{array}{c|cccccccc} \REMTEXT{年数} & 0 & 1 & 2 & 3 & 4 & 5 \\ \hline \REMTEXT{人} & 100 & 117 & 126 & 133 & 135 & 136 \\ \hline \REMTEXT{人(前年からの増加分)} & - & 17 & 9 & 7 & 2 & 1 \\ \end{array} $$
ユーリ「えーと、 $1$ 年目の $17$ 人は、 $117 - 100$ ってこと?」
僕「そうだね。 $0$ 年目は前年を考えないから、何もなし。 $-$ とだけ書いた. あとの $17,9,7,2,1$ は、それぞれ $117-100, 126-117, \ldots$ として……」
ユーリ「階差数列だ!」
僕「あ、そうなるね。前年からの増加分」
ユーリ「それで? これが何になるの?」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 430本すべての記事が読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2015年7月31日)
この記事は『数学ガールの秘密ノート/やさしい統計』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!