第105回 シーズン11 エピソード5

ラティス・サラダ（前編）

図書室にて

ミルカ「テトラは？」

僕「いや、知らないけど……今日は来てないね」

ミルカ「ふうん……」

僕「……」

ミルカ「どうした？」

僕「何でもないよ……」

ミルカ「……」

僕「……」

ミルカ「……」

僕「ミルカさん、顔赤くない？」

ミルカ「自分の顔色なんて見えない」

僕「そういう意味じゃなくて、熱っぽくないの？」

ミルカ「そういう自覚は特にないな」

僕「だったらいいけど。……そういえば、村木先生のカード、今回はあまりおもしろくなかったよ」

ミルカ「どれ？」

僕「これ」

ミルカ「ふうん……それで？」

僕「これは $2$ 進数だよね。こんなふうにまとめたほうが見やすくなる」

ミルカ「……」

僕「$4$ 桁だから $4$ ビット。 $0000$ から $1111$ までの $16$ 通り。 それぞれのビットは $0$ か $1$ かの $2$ 通りだから、 $4$ ビットで $2^4 = 16$ 通りになって計算も合ってる。 《もれなく、だぶりなく》」

ミルカ「ふむ。その点に異議はないが」

僕「だから、そこまでの話をかんたんにまとめて村木先生に持っていくつもりだよ。明日かな。 ところで、いま僕が計算しているのは指数関数の」

ミルカ「順序はどう見る？　それから演算も」

僕「何の話？」

ミルカ「君はこの $4$ ビットのパターンを見て、 $0000$ から $1111$ までの $16$ 通りと見た。 そこまでなら、もっと単純な表でもいいはずだろう？」

僕「単純な表というのは、たとえばこういうもの？」

ミルカ「そういうもの」

僕「まあ、そうだなあ……確かにこの村木先生の描き方は意味ありげだよね」

ミルカ「数えるのが好きな君が見逃しているのはおかしいな」

僕「え？　見逃しているわけじゃないよ。 $4$ ビット中の《$1$ の個数》のことだよね？　もちろん気付いているよ。 《$1$ の個数》が同じビットパターンは同じ行にまとまっている」

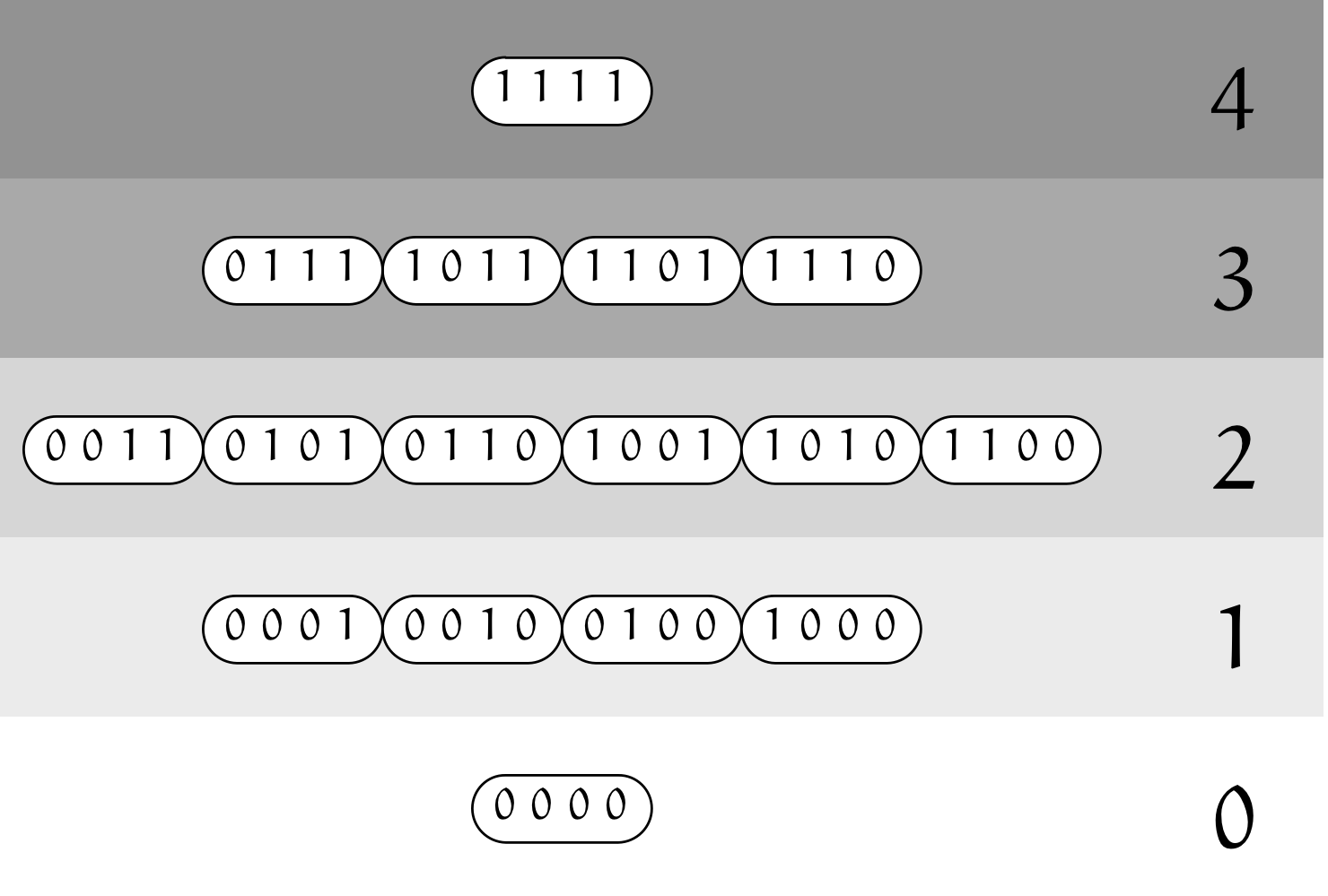
ミルカ「気付いていたのか」

僕「もちろんだよ。一番下が《$1$ が $0$ 個のビットパターン》で、上に行くごとに $1$ ずつ増えて、 $0,1,2,3,4$ となってる。 一番上が《$1$ が $4$ 個のビットパターン》」

ミルカ「一番下が最小値、一番上が最大値」

僕「うん、そうだね。《数える》という意味では、こういうのもあるよ。 $1$ の個数じゃなくて、各行ごとに《ビットパターンの個数》を数える。 上からでも、下からでも、 $1,4,6,4,1$ になる。この数のパターンは明らかだよね。二項係数だ」