![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/ビットとバイナリー』として書籍化されています。
登場人物紹介
僕:数学が好きな高校生(今回はインフルエンザでお休み)。
ユーリ:僕のいとこの中学生。僕のことを《お兄ちゃん》と呼ぶ。
テトラちゃん:僕の後輩。好奇心旺盛な《元気少女》。
ミルカさん:数学が好きな高校生。僕のクラスメート。長い黒髪の《饒舌才媛》(今回はインフルエンザでお休み)。
リサ:自在にプログラミングを行う無口な女子。赤い髪の《コンピュータ少女》。
読者のみなさん、こんにちは。テトラです(ぺこり)。
いつもご愛読ありがとうございます。
本日は先輩がインフルエンザでお休みなので、
あたしが語り部となります。どうぞよろしくお願いいたします。
それでは前編のあらすじですが、
あたしとユーリちゃんは、いま双倉図書館のイベントに来ています。
コンピュータに詳しいリサちゃんに解説してもらいながら、
スキャナとフィルタとプリンタで楽しんでいるところです。
前編の最後ではリサちゃんが「応用問題」を出題してくれました(第103回参照)。
後編はその場面からになります。
解説パネル(フィルタ)
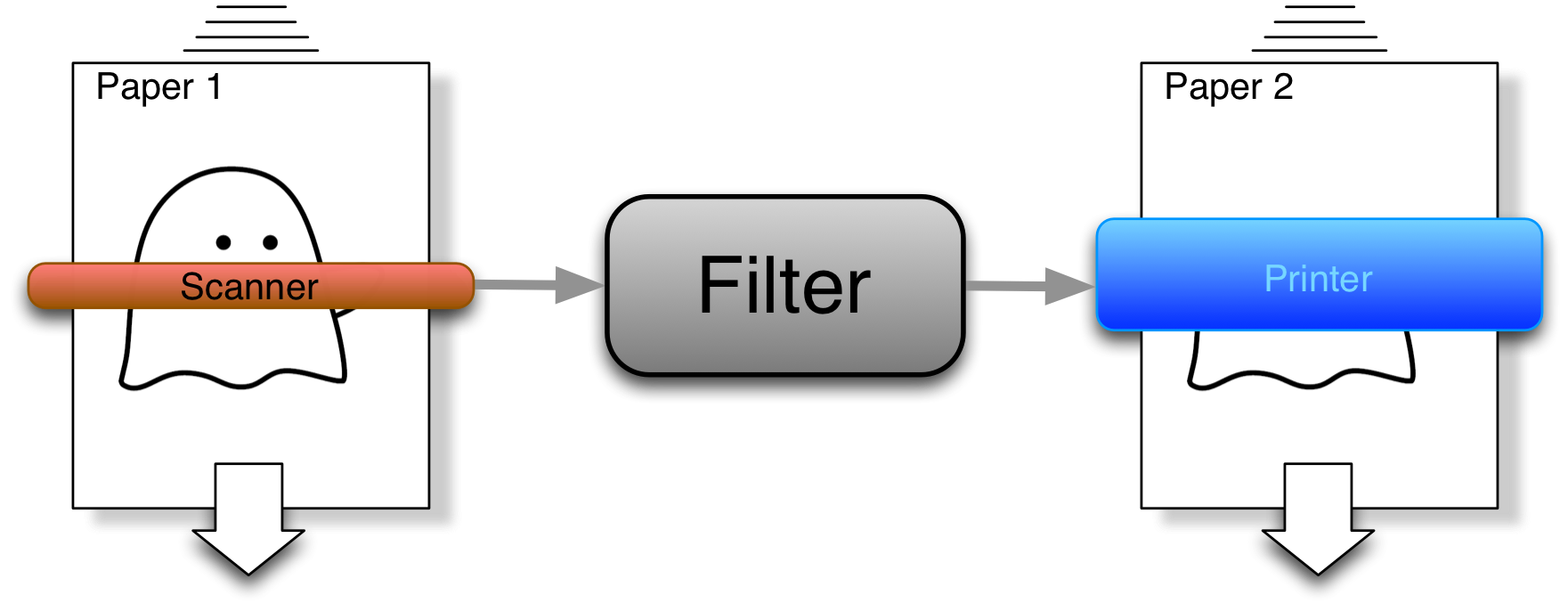
リサ「応用問題」
解説パネル(問題)
次のように画像を変形するには、 どんなフィルタを作ればいいでしょうか。

左側は、フィルタがスキャナから受信する画像です。
右側は、フィルタがプリンタに送信する画像です。
ユーリ「わかったよ、簡単!」
テトラ「ユーリちゃん、早いですね……あ、あたしはまだ」
ユーリ「これはねー、左右を逆転すればいーんだよ! こんな感じだよね」

テトラ「それはそうなんですけど、 フィルタが受信した《数》で行うにはどうするか、 が問題なんだと思いますよ。 どういう計算をすればこのような逆転ができるんでしょう」
ユーリ「それはねー……これから考える」
テトラ「あっ、そうです! こういうときこそ、ポリア先生の問いかけを使うべきですね。 たとえば《似た問題を知っているか》」
ユーリ「知ってる! ほらさっき、右 $8$ 個と左 $8$ 個を交換したじゃん?(第103回参照) それと同じよーにすればいーんだよ」
テトラ「はい、あのときは $f \gg 8$ で $8$ ビットを右にざざざざっと動かしましたね……」
ユーリ「だったら、 $f \gg 15$ にすれば、左端の $f_{15}$ は一番右に来るね!」

テトラ「はい。同じように、 $f \ll 15$ にすれば、右端の $f_{0}$ は一番左に来ます。 それはいいんですが……」
ユーリ「$f \gg 13$ にすれば、 $f_{14}$ は右から二番目に動くよ……あ」
テトラ「それじゃ、だめですよね。 $f_{14}$ は確かに右から二番目になりますが、 $f_{15}$ と $f_{13}$ が残ってしまいます」

ユーリ「そっかー! 《$f_{14}$ だけ取り出すこと》ができればいいのに」
リサ「論理積」
論理積(ビット単位) $$ \begin{align*} 0 \mathrel{\&} 0 &= 0 && \\ 0 \mathrel{\&} 1 &= 0 && \\ 1 \mathrel{\&} 0 &= 0 && \\ 1 \mathrel{\&} 1 &= 1 && \REMTEXT{両方が$1$のときだけ$1$} \\ \end{align*} $$
テトラ「論理積は、両方が $1$ のときだけ $1$ ですね……わかりましたよ。 これを使えば、 $f_{14}$ だけ取り出せます」
ユーリ「どーやるの?」
テトラ「$( 0000 0000 0000 0010)_2 $という数との論理積を作るんですよ! そうすれば右から二番目だけが残りますから!」

ユーリ「なーる!」
リサ「まとめたプログラム」
左右反転フィルタFILTER-REVERSE

テトラ「これは……何だかすさまじいですね」
リサ「ループにまとめたプログラム」
左右反転フィルタFILTER-REVERSE-LOOP(ループを使った)

テトラ「え、これは……」
リサ「同じフィルタ」
テトラ「FILTER-REVERSEとFILTER-REVERSE-LOOPは同じ……なんですか」
ユーリ「さっきとずいぶん違うみたい。 FILTER-REVERSEだとシフトが $16$ 個もあったけど……」
リサ「$\textit{RL7}$からのインナーループで」
テトラ「シフトは$\textit{RL11}$と$\textit{RL12}$にありますね……」
ユーリ「$(f \gg S) \mathrel{\&} R$ と $(f \ll S) \mathrel{\&} L$ のこと?」
テトラ「文字がたくさん出てきてよくわからないんですが、 たとえば、 $j = 0$ のときはどうなるんでしょう」
FILTER-REVERSE-LOOPで、 $j = 0$ のとき
$$ \left\{\begin{array}{llll} L &= 1 \ll (15 - 0) &= ( 1000 0000 0000 0000)_2 \\ R &= 1 \ll 0 &= ( 0000 0000 0000 0001)_2 \\ S &= 15 \\ \end{array}\right. $$
$j = 0$ のときのシフトのようす
$$ \left\{\begin{array}{llll} (f \gg S) \mathrel{\&} R & = (f \gg 15) \mathrel{\&} ( 0000 0000 0000 0001)_2 \\ (f \ll S) \mathrel{\&} L & = (f \ll 15) \mathrel{\&} ( 1000 0000 0000 0000)_2 \\ \end{array}\right. $$
ユーリ「うわすごい! これで、右端と左端が取り出せてる!」
テトラ「ははあ……FILTER-REVERSE-LOOPの $\textit{RL7}$からの繰り返し$8$回が効いているんですね」
ユーリ「リサさんすごい!」
リサ「《さん》は不要」
テトラ「鏡のように左右を逆にするだけのことなのに、複雑なプログラムになるんですね……」
リサ「トリック使用」
ユーリ「トリック?」
左右反転フィルタFILTER-REVERSE-TRICK(トリックを使った)

テトラ「え?」
ユーリ「え?」
リサ「$M_1,M_2,M_4,M_8$と$\textit{RT9}$からがトリック」(咳)
テトラ「これは……何をやっているんでしょう」
ユーリ「あれ? FILTER-REVERSEにあった $g$ がなくなってる」
テトラ「$f$を、$\textit{RT9}$からの$4$行で書き換えているんだと思うんですが……」
ユーリ「テトラさん、図に描いて研究しよーよ!」
テトラ「そ、そうですね……」
あたしとユーリちゃんは、リサさんが《トリック》と呼んだFILTER-REVERSE-TRICKを解読するため、 二人で図を描いて……心の底から驚きました。
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 430本すべての記事が読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2015年1月30日)
この記事は『数学ガールの秘密ノート/ビットとバイナリー』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!