第73回 シーズン8 エピソード3

大きくなる？小さくなる？（前編）

図書室で

テトラ「テトレーション……？」

僕「そうそう。テトレーションという名前がついているんだよ、それ」

テトラ「まるで私の計算みたいですねっ！」

僕「そうなんだよ。ユーリも『テトラさん？』なんて言ってた。 テトレーションという名前は加算→乗算→冪乗→テトレーションという順番で $4$ 番目だからそんな名前がついたんだよ」

テトラ「なるほど $4$ 番目で"tetra"なのですね。"tetration"ということは……ええと、"tetra + inflation" でしょうか」

僕「インフレーション？　いや、村木先生はテトラ＋イテレーションと言ってたかな」

テトラ「ふむふむふむふむ！ "tetra + iteration" で "tetration" ですか」

僕「でも、そこまではグッドシュタインの論文には書いてないそうだけど。Wikipedia情報」

テトラ「それにしても冪乗（べきじょう）の繰り返しってすごく大きくなるんですね」

僕「そうだね。繰り返さない冪乗でもすごく大きくなるんだけどね」

テトラ「放物線はぐーんと伸びていきますものね」

僕「え？」

テトラ「え？　ほ、放物線のグラフですよね？」

僕「……ああ、まあね。放物線のグラフ $y = x^2$ に出てくる $x^2$ も冪乗といえば冪乗だけど」

テトラ「何か、おかしかったでしょうか？」

僕「さっき話してた加算→乗算→冪乗→テトレーションというときの冪乗では、指数のところに変数が来るんだよ」

テトラ「はい」

僕「テトラちゃんがいま言った放物線を作るのは $x^2$ だから、 $2^x$ とは違うよね。 $x^2$ では底（てい）が変数 $x$ になっていて、 $2^x$ では指数が変数 $x$ になってる」

テトラ「ははあ……そうですね。勘違いしていました。すみません」

僕「実際ね、 $x^2$ と $2^x$ とではまったく違うんだよ。 $y = x^2$ と $y = 2^x$ のグラフを描いてみるとよくわかる」

テトラ「$y = x^2$ のグラフはこうですよね？　放物線」

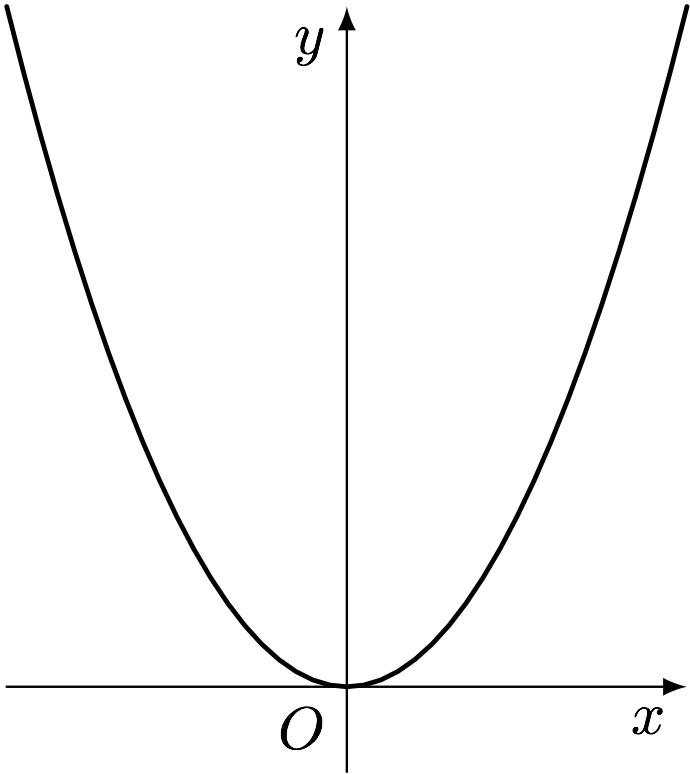
僕「そうそう。原点を通って下に凸の放物線になるね。左右対称だ。でも、これに対して $y = 2^x$ のグラフはぜんぜん違うよ」

テトラ「これはなんていう線なんですか？」

僕「え？　……あ、言われてみれば考えたことないなあ。指数関数が作る曲線とでもいうんだろうけど」

テトラちゃんはじっと $y = 2^x$ のグラフを見ている。

テトラ「この曲線は左右対称にはならないんですね。放物線と違って」

僕「そうだね。 $y = x^2$ のような放物線が左右対称になる理由はわかる？」

テトラ「ええと……はい、わかります。 $2$ 乗になっているからですね」

僕「そうだね。 $x$ がどんな実数だったとしても、 $x$ を $2$ 乗した数と、 $-x$ を $2$ 乗した数は必ず等しくなる。 つまり、 $x^2 = (-x)^2$ が成り立つ。ということは《$y = x^2$ のグラフ》と、 $y$ 軸でそのグラフを左右反転した《$y = (-x)^2$ のグラフ》はぴったり重なることになる」

テトラ「はい」

僕「でも、 $y = 2^x$ ではそんなことは起きないし」

テトラ「……なるほどです。あの、先輩？」

僕「なに？」

テトラ「あたしは『$2$ 乗になっているから』で終わらせてしまいましたけれど、 先輩は『$x^2 = (-x)^2$ だから……』のように式を使って説明してくださいますね」

僕「え、まあ、そうだけど？」

テトラ「あたしは、それをお聞きしてなるほどと思いました。 先輩はいつもグラフのお話をするとき、式と関連づけてお話になる、というところです」

僕「へえ……でも、式と関連づけないと何だかしっくりこないから」

テトラ「そうなんですね」

僕「ところでテトラちゃん、この $y = 2^x$ のグラフの左側……つまり $x$ がマイナスでとても小さくなったときって、 どうなると思う？」

テトラ「このグラフの線ですか？　左側にずうううううっと行って、 すごくすごくすごくすごく $x$ 軸に近づくことになると思います。 ……で、いいですか？」

僕「そうそう、それでいいよ。 $x$ を小さくしていくと《いくらでも》$2^x$ は $0$ に近づいていく。 でも決して $2^x$ は $0$ に等しくならない」

テトラ「はい、わかります。漸近線（ぜんきんせん）ですね」

僕「そう！　 $x$ 軸は $y = 2^x$ のグラフの漸近線になっている。 僕は初めて漸近線のことを聞いたとき、すごく不思議だったんだ。確か $y = \dfrac{1}{x}$ の反比例のグラフだったけど」

テトラ「不思議といいますと」

僕「だって、いくらでも $0$ に近づくけど、決して $0$ にならない数って不思議じゃない？」

テトラ「確かに……言われてみればそうですね。あれ、先輩？　逆に、 $y = 2^x$ で $x$ が大きくなったときには何に近づくんですか？」

僕「え？　いや、 $y = 2^x$ で $x$ が大きくなったときには $2^x$ はいくらでも大きくなるし、漸近線もないよ。 $x$ 軸からどんどん離れていくばかりだし」

テトラ「で、でも、漸近線ってどんな直線でもいいですよね」

僕「そうだね。曲線を考えるときもあるけど、普通は漸近線といったら直線。どんな直線でもいいけど」

テトラ「軸でなくてもいいですよね」

僕「うん。いいよ」

テトラ「だったら、この $y = 2^x$ のグラフにこんな直線を考えてはだめなんでしょうか。漸近線として」

僕「なるほどね。でもこれはだめだよ、テトラちゃん。だって、 $y = 2^x$ は $x$ が大きくなるとき、どんな直線よりも上に行くから」

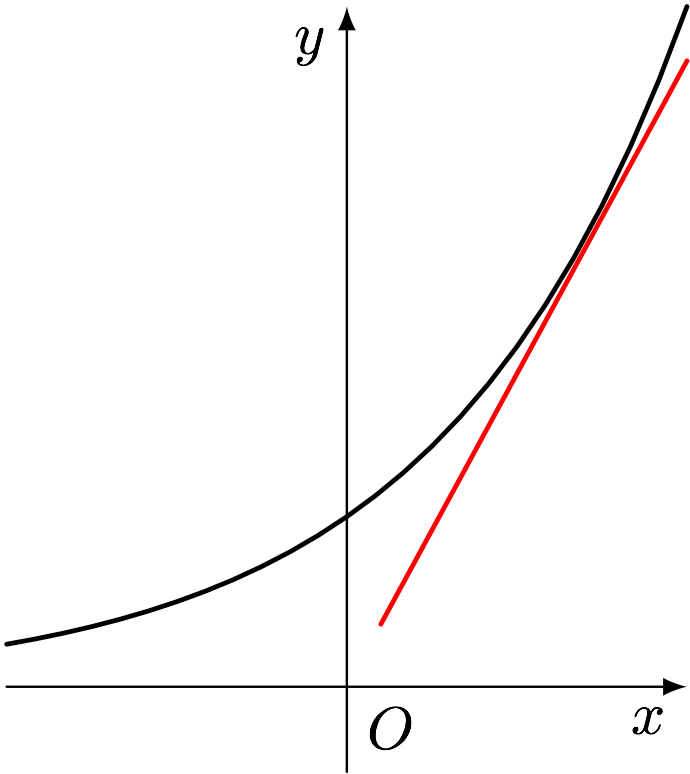
テトラ「そうなんですね。もっと大きな範囲で考えなくてはいけない……」

僕「直線に限らないよ。 $y = x$ よりも、 $y = x^2$ よりも、 $y = x^3$ よりも……つまり、 $y = x^n$ よりも $y = 2^x$ のグラフは上に行くことになる」

テトラ「そうなんですか……」

僕「$x$ が大きくなると、指数関数はそれだけものすごく大きくなるってことだね。 $x^n$ のように底のほうに変数が入っているのと、 $2^x$ のように指数のほうに変数が入っているのとでは、 まったく意味が違うんだよ」

テトラ「なるほどです。よくわかりました」

底を変える

僕「$2^x$ で変数 $x$ が指数のほうに入っているといったけど、 もちろん、底の方を変えることもできるよ」

テトラ「えっ？」

僕「つまりね、 $2^x$ を $a^x$ という形をしている式だと思って、 $a$ の値をいろいろと変えてみるということ。 $2^x$ の $2$ を $a$ にしたわけだから、 これは《文字の導入による一般化》だね」

テトラ「両方いちどに変えてしまったら大騒ぎになりませんか？」

僕「いやいや、そんなことはないよ。だって、ある $a$ の値に対して、 $y = a^x$ のグラフは一本の曲線だよね」

テトラ「えっと、それはそうですね。 $y = 2^x$ の曲線のように？」

僕「そうそう。それで、いくつかの $a$ の値でグラフを描いてみたら、そういう曲線が何本も描かれるだけだよね」

テトラ「ははあ……それはそうですけれど。 いえ、あの、文字が増えて、それを変化させるというのでちょっとドキドキしているだけです」

テトラちゃんはそういって、両手を胸に当てる。

そうだった。テトラちゃんは文字が多くなってくるとすぐに不安になるんだった。

僕「大丈夫だよ。 $a \leqq 0$ だと話がややこしくなるから、いまは $a > 0$ であるとしよう。 $a$ は正の数。それで $y = a^x$ のグラフを考えてみよう」

テトラ「はい、わかりました。……あれ？　でもよく考えてみれば、 $y = 2^x$ のグラフと似ている形になりますよね。だって、 $y = a^x$ で、 $a$ が大きくなればそれだけ急激に大きくなるわけですから」

僕「うんうん、それで？」

テトラ「それで、たとえば $a$ が $3, 4, 5, \ldots$ だとすると、 $y = a^x$ のグラフは、 $y = 2^x$ のぎゅーんと増えていくグラフよりも上になりますよね」

僕「テトラちゃん、それは $y = 2^x$ のグラフよりも、 $y = 3^x$ のグラフの方がいつも上にくるという意味かなあ？」

テトラ「え、はい、そうです。だって、たとえば $x = 2$ のとき。 $2^x = 2^2 = 4$ で、 $3^x = 3^2 = 9$ ですよね？　 $4 < 9$ になっています。 それからたとえば、 $x = 3$ のとき。 $2^x = 2^3 = 8$ で、 $3^x = 3^3 = 27$ ですから、やっぱり $8 < 27$ です。 $2^x$ よりも $3^x$ のほうが、いつも上になるのではないでしょうか？」

僕「$x > 0$ だったら、そうなるね」

テトラ「はい？」