![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png)
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート／ベクトルの真実』として書籍化されています。
僕とユーリは簡単なベクトルの問題を使って数学トークをしている。 $\dfrac{\vec a + \vec b}{2}$ というベクトルの終点が、 $\vec a$ と $\vec b$ の終点を結んだ線分の中点になることを証明したところ。
僕「ベクトルを使うと、図形の問題も式変形や計算に持ち込めるってことを言いたかったんだけど……」
ユーリ「でも、やっぱりめんどいよー」
僕「……でもほら、座標の計算すらせずに、中点だといえるし」
ユーリ「あ、確かにそれはそーだね」
僕「だろ？ 似た問題としては、こんなのもあるよ。いいかい……」
ユーリ「（しまった）」
問題1
平面上の二点 $A$ と $B$ がある。 線分 $AB$ を $m:n$ の比で内分する点を $P$ としたとき、 ベクトル $\vec{OP}$ を $\vec{OA}$ と $\vec{OB}$ を使って表せ。
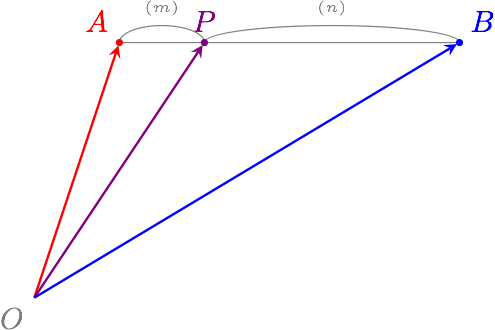
僕「こんな問題はどうかな、ユーリ」
ユーリ「エムたいエヌの比でないぶんする点……」
僕「そうそう。内分点というときもあるね」
ユーリ「とりあえず、さっぱりわかんないんだけど」
僕「そう？ わからないときには《似ている問題を知っているか？》と自分に問いかけるんだよ。 たとえば、 $m:n = 1:1$ のときはわかるよね」
ユーリ「わかんない」
僕「ねえ、ユーリ。『そのスピードは考えてない証拠』ってミルカさんに言われたんじゃなかったっけ？」
ユーリ「ちぇっ！ えーと……エムたいエヌがイチたいイチ……あ、なーんだ中点じゃん！ さっきやったよ。こーでしょ？」
内分点の特別な場合（中点）
平面上の二点 $A$ と $B$ がある。 線分 $AB$ を $1:1$ の比で内分する点を $P$ としたとき、 ベクトル $\vec{OP}$ は $\vec{OA}$ と $\vec{OB}$ を使って次のように表せる。
$$ \vec{OP} = \dfrac{\vec{OA} + \vec{OB}}{2} $$
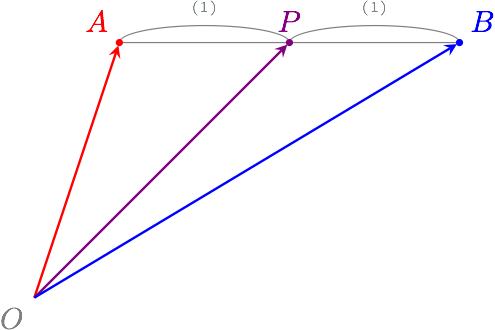
僕「その通り！ そうだね。線分 $AB$ の中点は、いいかえれば $1:1$ に内分する点ということになる。 そしてそれは、二つのベクトル $\vec{OA}$ と $\vec{OB}$ を足して $2$ で割った……平均の形になる」
ユーリ「ふんふん。そんで？」
僕「だからね、さっきの《$m:n$ に内分する点を求める》という問題は、 《中点を求める》という問題を一般化していることになるんだよ」
ユーリ「いっぱんか……」
僕「そうだよ。《文字の導入による一般化》だ。 $m$ と $n$ の二つの文字が出てきて一般化してる」
ユーリ「ふーん」
僕「中点を求める問題を $m:n$ の内分点を求める問題に一般化した。 でね、こういうときには一般化する前の問題をよく見て、どうすれば一般化した問題が解けるかなって考える。 もう手元に解いた問題があるから考えやすいよね」
ユーリ「でもね、お兄ちゃん。 $1:1$ と $m:n$ じゃずいぶん違うよ」
僕「こんなふうに考えてみようか。 $1:1$ じゃなくて $1:2$ に内分する点はどうなるかな」
ユーリ「？」
僕「つまりね、 $m:n$ みたいに文字で考えるんじゃなくて、 $1:2$ という別の具体的な問題を考えてみるんだよ。 もちろん、 $1:1$ のときの答えが大きなヒントになる」
ユーリ「イチたいニの点……」
問題2
平面上の二点 $A$ と $B$ がある。 線分 $AB$ を $1:2$ の比で内分する点を $P$ としたとき、 ベクトル $\vec{OP}$ を $\vec{OA}$ と $\vec{OB}$ を使って表せ。
僕「さあ図形問題だ。まず、最初にどうする？」
ユーリ「あ！ そだそだ。《図を描く》んだった」
僕「そうだね。線分 $AB$ を $1:2$ に内分する点 $P$ を描こう」
ユーリ「$1:2$ の点って $AP$ の方が短いんだよね……こうかにゃ？」
線分 $AB$ を $1:2$ に内分する点 $P$ を描く
僕「そうそう。それでいいね。さてそれで……」
ユーリ「それで？」
僕「《求めるものは何？》」
ユーリ「点 $P$ でしょ」
僕「じゃなくて、ベクトル $\vec{OP}$ だね」
ユーリ「あー！ ユーリ、そーゆー意味で言ったんだよ、いま！」
僕「はいはい。ともかく求めるものはベクトル $\vec{OP}$ だね。さてそれで……」
ユーリ「それで？」
僕「《与えられているものは何？》」
ユーリ「与えられているのは、点 $A$ と点 $B$ じゃん」
僕「ユーリは、それ、どういう意味で言ったの？」
ユーリ「おっと！ 与えられているのはベクトル $\vec{OA}$ と $\vec{OB}$ だよん、もちろん」
僕「そうだね。だから、 $\vec{OA}$ と $\vec{OB}$ を使って $\vec{OP}$ を表せば問題解決」
ユーリ「……」
僕「どうした？」
ユーリ「考えてんの！ ……あのね、単純に $\vec{OA}$ と $\vec{OB}$ の平均にしたら、 中点になっちゃうわけだよね？」
僕「そうそう、いいぞ」
ユーリ「$1:1$ じゃなくて $1:2$ にしたいんだから、 点 $P$ は中点よりも点 $A$ に近くしなくちゃいけないんだよね？」
僕「そうだね」
ユーリ「だから……あのね、平均みたいなことをするんだけど、 $\vec{OA}$ をね、エラくすればいいと思うんだけど」
僕「偉くする？」
ユーリ「エラくするってゆーか、強くするってゆーか……とにかく $\vec{OA}$ の方を $\vec{OB}$ よりも二倍くらい 強くしてやるといいんじゃないかなって」
僕「すごいな、ユーリ！それで正解だよ。《重くする》というんだけど、 ユーリの考えで正解だよ」
ユーリ「え、ほんと？ じゃ、こうだ！」
ユーリの解答
平面上の二点 $A$ と $B$ がある。 線分 $AB$ を $1:2$ の比で内分する点を $P$ としたとき、 ベクトル $\vec{OP}$ は $\vec{OA}$ と $\vec{OB}$ を使って次のように表せる。
$$ \vec{OP} = \dfrac{2\vec{OA} + \vec{OB}}{2} \qquad \textbf{（？）} $$
僕「うわ、惜しい！」
ユーリ「違うの？」
僕「分母は $2$ じゃなくて $3$ になるんだよ。 ほら、 $\vec{OA}$ は $2$ つ分の重みで、 $\vec{OB}$ は $1$ つ分の重みで考えたんだから、 全体としては $3$ の重みで割ってやる必要がある」
ユーリ「あ！ なるほど！」
解答2
平面上の二点 $A$ と $B$ がある。 線分 $AB$ を $1:2$ の比で内分する点を $P$ としたとき、 ベクトル $\vec{OP}$ は $\vec{OA}$ と $\vec{OB}$ を使って次のように表せる。
$$ \vec{OP} = \dfrac{2\vec{OA} + \vec{OB}}{3} $$
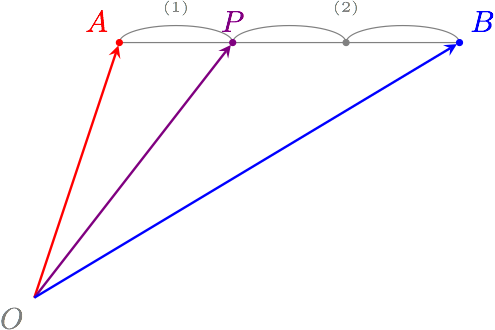
僕「それにしても、よくわかったね」
ユーリ「うーん……でも……」
僕「$1:1$ と $1:2$ がわかったってことは、 もう $m:n$ も予想がつくんじゃないかな？」
ユーリ「あ……」
ユーリは急に口を閉じ、真剣な顔つきになる。 栗色の髪が金色に輝く。
僕「……」
ユーリ「……わかった！ $m$ 倍と $n$ 倍重くすればいい……違う、逆！ $n$ 倍と $m$ 倍！」
僕「おお！」
ユーリ「そんで、 $m+n$ で割るんでしょ？ こうだ！」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 434本すべての記事が読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方／すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加（2014年1月3日）
この記事は『数学ガールの秘密ノート／ベクトルの真実』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ！
![[icon]](https://img.hyuki.net/20220619121014-abd58cfc2ab436f4.png)