![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」

登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。 好奇心旺盛で根気強い《元気少女》。言葉が大好き。
後輩のテトラちゃんと僕の二人は、放課後の図書室で《数学トーク》を続けていた。
いまは、取り組んでいた問題の解答も得られ、 テトラちゃんの疑問も晴れて、 AIとの《対話》も一段落したところだ(第455回参照)。
……そうか、《数学トーク》をしていたのは二人じゃないんだな。
テトラちゃんと僕だけじゃなくて、AIもいる。
《数学トーク》を続けているのは、 AIを含めた三人なのだ。
テトラ「いま、ふと思ったことがあるんですが、聞いていただけますか?」
僕「もちろん。どんなこと?」
テトラ「先ほど解いていた数学の問題、あたしはネットで見つけました(第455回参照)」
僕「うん」
テトラ「あたしたちは、よく数学の問題を解きますよね」
僕「そうだね」
テトラ「授業や宿題で出た問題を解くこともありますし、 村木先生からいただいた《カード》で出された問題を解くこともあります」
僕「村木先生の《カード》だと、 問題になってなくて、 僕たちが自分で作ることもあるよ」
テトラ「ですです!」
村木先生の《カード》に限らず、 自分で問題を作って解くことは珍しくない。
実際よくあるのだ。
数学で問題を解いていて「へえ、こんなことが成り立つんだ。面白いな」と考える。 そして「だとしたら、こういうことも成り立つんじゃないかな」という気持ちになる。 自分で問題を作ってそれを解く。それは実際、よくあることだ。
まあ、解けないこともよくあるんだけど。
僕「それで、数学の問題がどうかしたの?」
テトラ「はい。あたしが思ったのはですね。 AIさんは——」
テトラちゃんはそこで、ハッと何かに気づいたように手を動かし、 いままでコンピュータでAIとチャットしていたウインドウをすばやく閉じた。
僕「何? どうしたの?」
テトラ「あ、いえ、 何だか、 AIさんに話を聞かれてるみたいだったので、 いったん閉じさせてもらいました……」
テトラちゃんは、急に声をひそめ、僕に顔を近づけてそう言った。 まるで、内緒話でも始めるかのように。
僕はちょっとドキドキする。
僕「それで……?」
テトラ「はい。 あたしが思ったのは、 AIは数学の問題を出すことができるのか? ということです」
僕「え? それは普通にできるんじゃないの? さっきみたいに三角関数の問題を解けるんだから、 AIが問題を出題しても何もおかしくないよね(第455回参照)」
テトラ「ええ、それはそうなんですが、 AIさんは、ちょうどいい問題を出してくれるだろうか? というのが気になったんです」
僕「ちょうどいい問題?」
テトラ「そうですっ! 難しすぎず、 易しすぎず、 興味を持って解くことができて、 学ぶことも多い。 夢中になるくらいおもしろくて、 でもその問題で終わりにはならずに『もっと学びたい!』と思えるような、 そんな問題です」
僕は苦笑した。
僕「ずいぶんハードル上げるなあ……そこまで『ちょうどいい問題』を出すというメタな問題になると、 さすがに難問かもしれないね。 超・難問だ。 だって、 一度に授業を受けてるクラスメートはたくさんいるんだから、 みんなにぴったりあった問題を出すなんて無理じゃないのかな?」
テトラ「いえいえ、違いますよ、 先輩。 クラスのみんなに問題を出すという話じゃありません。 AIさんはあたし一人に問題を出すんです」
僕「なるほど?」
テトラ「AIさんには、 そういうことができるでしょうか?」
僕「うーん……」
テトラ「さっき、チャットウインドウを閉じたのは、 『AIさんにできるのか』という話題を、 AIさん自身の前で話すのは失礼かなと思ったからです」
僕「音声対話モードにしなければ、 僕たちの声はAIにも聞こえないよ。 もっとも、仮にAIが聞いたとしても失礼とは思わないだろうけど」
テトラ「あ、ええ、そうですね。AIがどう感じるかというより、 あたしがそう感じたからなんです。 ともかく、AIさんが、 あたしにちょうどいい問題を出してくれたら楽しいなと思いましたっ!」
僕は少し考えた。そして言った。
僕「うまくいくかどうかはわからないけど、試してみたらどうだろう。 テトラちゃんの方から『このぐらいの難しさの問題を出して』と言えば、 そういう問題が出てくると思うよ。 さっきみたいにハードルを上げてもいいね。 がんがんハードル上げたら、 どんな問題を出してくるだろう……僕も興味あるよ」
テトラ「ああ、なるほどです! どういう問題を出してほしいかというところも、 自分から指示しちゃえばいいんですね!」
僕「そうだね。 AIにどういう指示を出せばいいか と考えるところから、 すでにおもしろいよ。 たとえば『三角関数の問題を出して』と指示するのか、 もっと細かく『三角関数の加法定理の問題を出して』と指示するのか、 さらに具体的に指示するのか」
テトラ「あたしは分野や単元を指定しない問題をイメージしていました」
僕「『高校生向けの問題を出して』とか? そうすると定期試験風じゃなくて、実力試験風の問題になりそうだね」
テトラ「あたしがお願いするまで解答は絶対に見せないでください、 という指示もできそうです」
僕「さっそくAIに何か問題を出してもらおうよ。 テトラちゃんはどんな問題がいいの? 難しすぎず、易しすぎず——だっけ」
テトラ「そうですねえ……」
テトラちゃんは、 さっき閉じたウインドウを開き直し、AIと対話を始めた。
テトラ「AIさん、 さっきは急にウインドウを閉じてごめんなさい」
AI「テトラさん、大丈夫ですよ。 今回はどんなお話をしましょうか。 どんなことでもお尋ねください」
テトラちゃんがテキストを入力し、 AIがテキストで答える。
コンピュータのウインドウを挟んで、二人の《対話》が始まった。
ウインドウのこちら側にはテトラちゃんがいる。 それは見えているからわかる。
ウインドウの向こう側にはAIがいる——いるはずだ。 でも、流れるテキストを読んでいるだけだと、 向こう側にいる《対話》の相手がAIなのか、 それとも人間なのか、それを見分けることは難しい。
テトラ「AIさんは、数学の問題をあたしに出題することはできますか?」
AI「テトラさん、はい、もちろんです! 数学の問題をあなたに出題すること、できますよ。 どんな分野の問題が良いですか? 今回扱ったような三角関数の方程式や、二次関数、図形の問題など、 あなたの学習状況や興味に合わせて問題を選べます。 難易度も調整できますので、希望があれば教えてくださいね。いつでも準備はできていますよ!」
テトラ「《不思議な結果》が出てくる数学の問題を解いてみたいです! あたしでも考えることができるくらいの、 ちょうどいい難しさで、 おもしろくて、 『数学を、もっと学びたい!』 と思えるような問題を出していただけますか?」
AI「テトラさん、面白いリクエストですね! 承知いたしました。 ちょうどいい難しさで、 数学をもっと学びたくなる《不思議な結果》が出てくる問題ですね。 それでは出題する前に、 私の方からいくつか質問をさせてください。 テトラさんは、 積分をご存じですか?」
思いがけず、AIの方から問い掛けがやってきた。
テトラちゃんは助けを求めるように僕を見る。
僕は「テトラちゃんの思った通りに返事したら?」と言ってコンピュータに手を向け、 入力を促す。
二人の《対話》が再開する。
テトラ「積分は、少しわかります。 簡単なものなら計算もできます。 でも、あまり難しい積分は分かりません」
AI「テトラさんは、極限についてはどうでしょう。 積分と極限を組み合わせた問題になると難しすぎるでしょうか?」
テトラ「極限についても、ある程度はわかります。 ああ、それにいま、 あたしのすぐそばには数学に強い先輩がいるので、 何とかなると思います。 でも、解答はすぐに見せないでください」
テトラちゃんはそんなふうにAIに返事すると、僕の方を見てにっこり微笑んだ。
《数学に強い先輩》と言われて悪い気持ちはしない。 でも、いつのまにかAIの出題する《不思議な結果》が出てくる問題に、 どうやら僕も挑戦することになったみたいだ。
AI「それでは『ガブリエルのラッパ』という問題をご紹介します。 回転体の体積と表面積を求める問題です。 積分と極限の知識があれば取り組むことができますし、 必要になる公式もヒントとして置いておきます。 テトラさんは、 数学に強い先輩といっしょに考えてみてください!」
テトラ「ガブリエルのラッパ?」
僕とテトラちゃんは、AIから出題された問題に注目する。
問題(ガブリエルのラッパ)
$1$ 以上の実数を定義域とする関数 $f(x)$ を $$ f(x) = \frac{1}{x} \qquad (x \GEQ 1) $$ で定義します。 $y = f(x)$ の曲線は次の図のようになります。
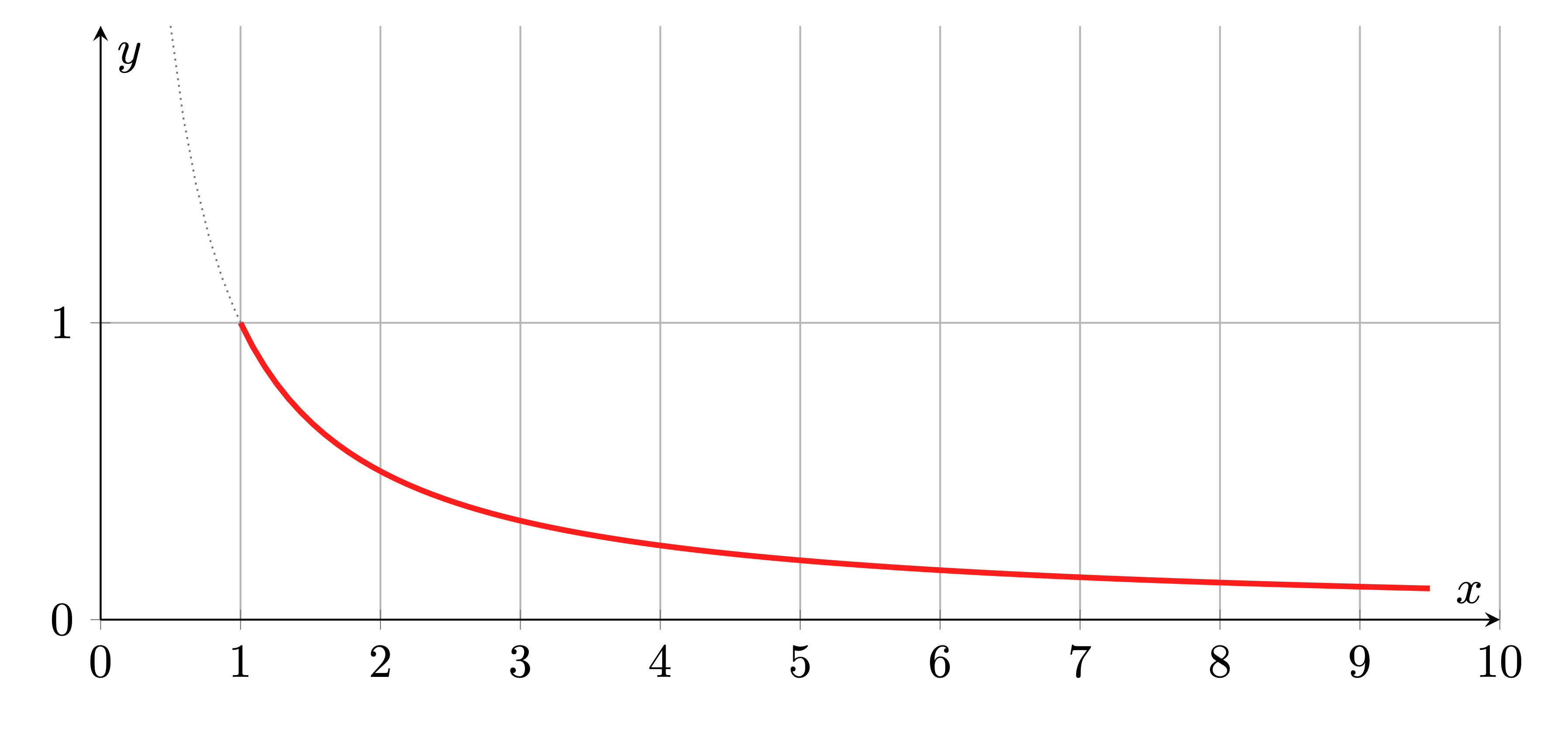
この曲線を $x$ 軸の周りに回転させてできる立体を $H$ とします。
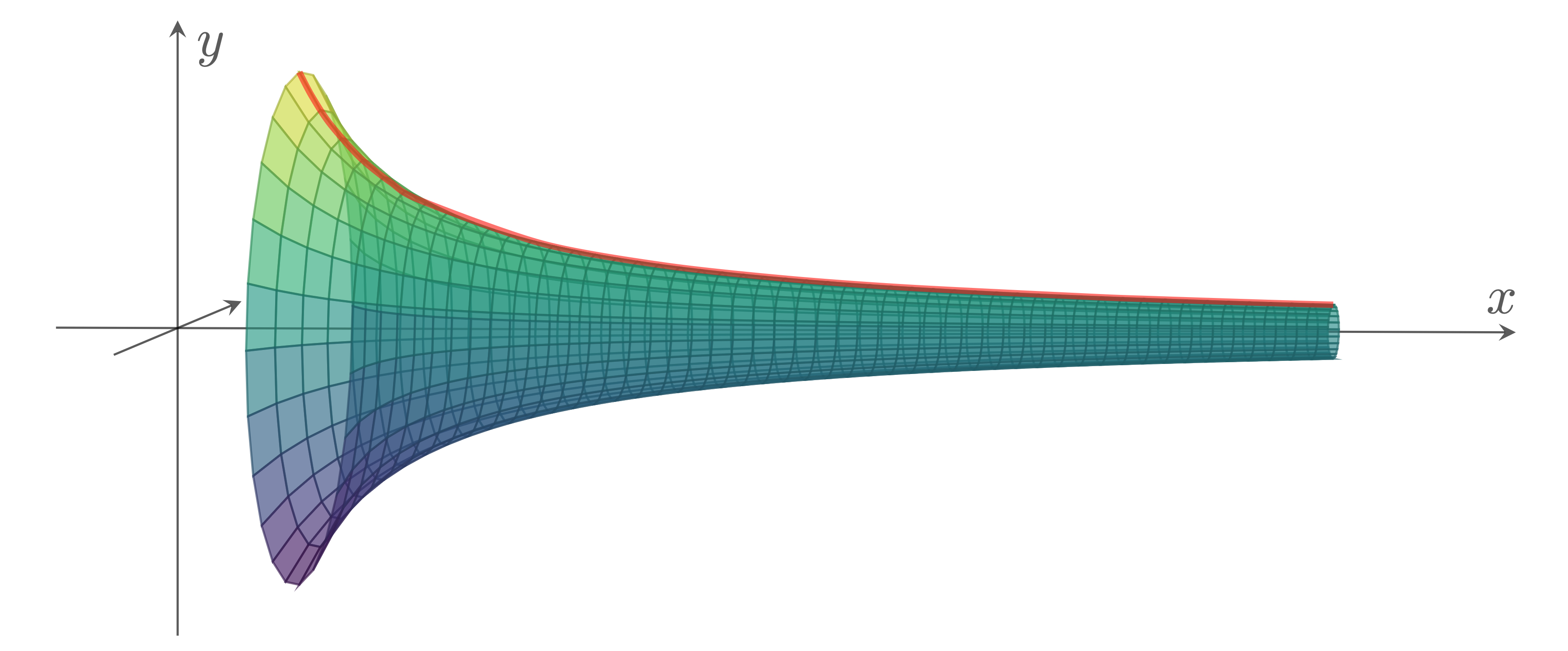
この立体 $H$ について、次の二つの問題に答えてください。
(1) この立体 $H$ 内部の体積を求めよ。
(2) この立体 $H$ の表面積を求めよ。
【ヒント】
$x = b$ までの回転体の体積 $V_b$ を求める式: $$ V_b = \pi \int_1^b \PS{f(x)}^2 dx $$
$x = b$ までの回転体の表面積 $S_b$ を求める式: $$ S_b = 2\pi \int_1^b f(x)\sqrt{1 + \PS{f'(x)}^2} dx $$
$V_b$ から $V$ を求める式:
$$ V = \lim_{b \to \infty} V_b $$
$S_b$ から $S$ を求める式:
$$ S = \lim_{b \to \infty} S_b $$
この問題を解くと、とても《不思議な結果》が待っています。ぜひ計算してみてください!
なお、この立体はガブリエルのラッパ(Gabriel's Horn)と呼ばれています。

テトラ「難しい問題が出てきてしまいました……」
僕「テトラちゃんが《数学に強い先輩》なんて持ち上げるからだと思うけど……でも、 おもしろそうだよ。 ああ、それにちゃんと【ヒント】がついてるから、 計算問題のレベルまで易しくなってるんだ」
テトラ「式に当てはめていけば解けるということでしょうか?」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2025年7月25日)