第440回 シーズン44 エピソード10

《九点平面》の世界（後編）

《九点平面》における平行

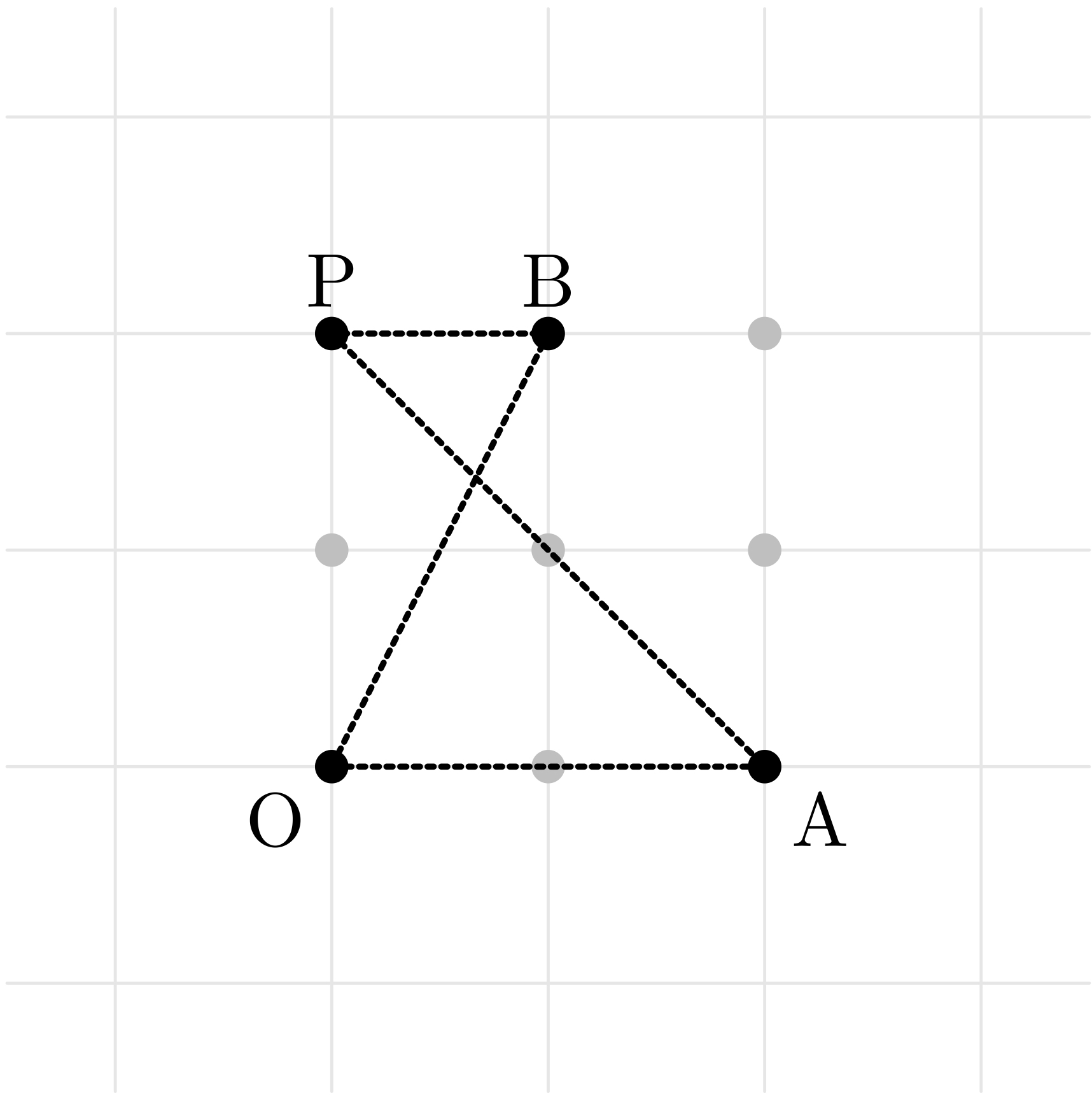
僕「この四辺形 $\TT{OAPB}$ は《いわゆる平行四辺形》には見えない。 $\TT{OA}$ と $\TT{PB}$ は平行に見えるけど、 $\TT{AP}$ と $\TT{OB}$ は平行に見えない。 でも《九点平面》での平行をベクトルで定義すればどうだろうか。 つまり、 $$ \vAP = k\vOB $$ という $k$ が存在すれば《九点平面》で $\TT{AP}$ と $\TT{OB}$ は平行と考えるということ」

テトラ「おもしろいですっ！　見た目では $\vAP$ と $\vOB$ はまったく平行じゃありません。 でも、 $\vAP = k\vOB$ を満たす $k$ が存在すれば $\vAP$ と $\vOB$ が平行——」

僕「そうだね。 それは、ベクトルを使ってこの《九点平面》における《いわば平行》を定義していることになる。 見た目ではなくて、数式を頼りにする」

テトラ「この問題1は、機械的に成分を計算してみればいいはずですよね？　では、やってみます」

僕「ちょっと待って。最後のところ、どうして《$k$ が存在しない》って思ったの？」

テトラ「だってそうですよね。 $$ \begin{cases} -2 &= k \\ 2 &= 2k \end{cases} $$ の両方を満たす $k$ は存在しません」

僕「$k$ が実数だったらそうだね。 でもいま僕たちは《九点平面》の世界にいる。 つまり、ここの $k$ は、 $k = 0,1,2$ のどれかになる。 成分の和もスカラー倍も、すべての計算は $3$ で割った余りで考えるんだよ！」

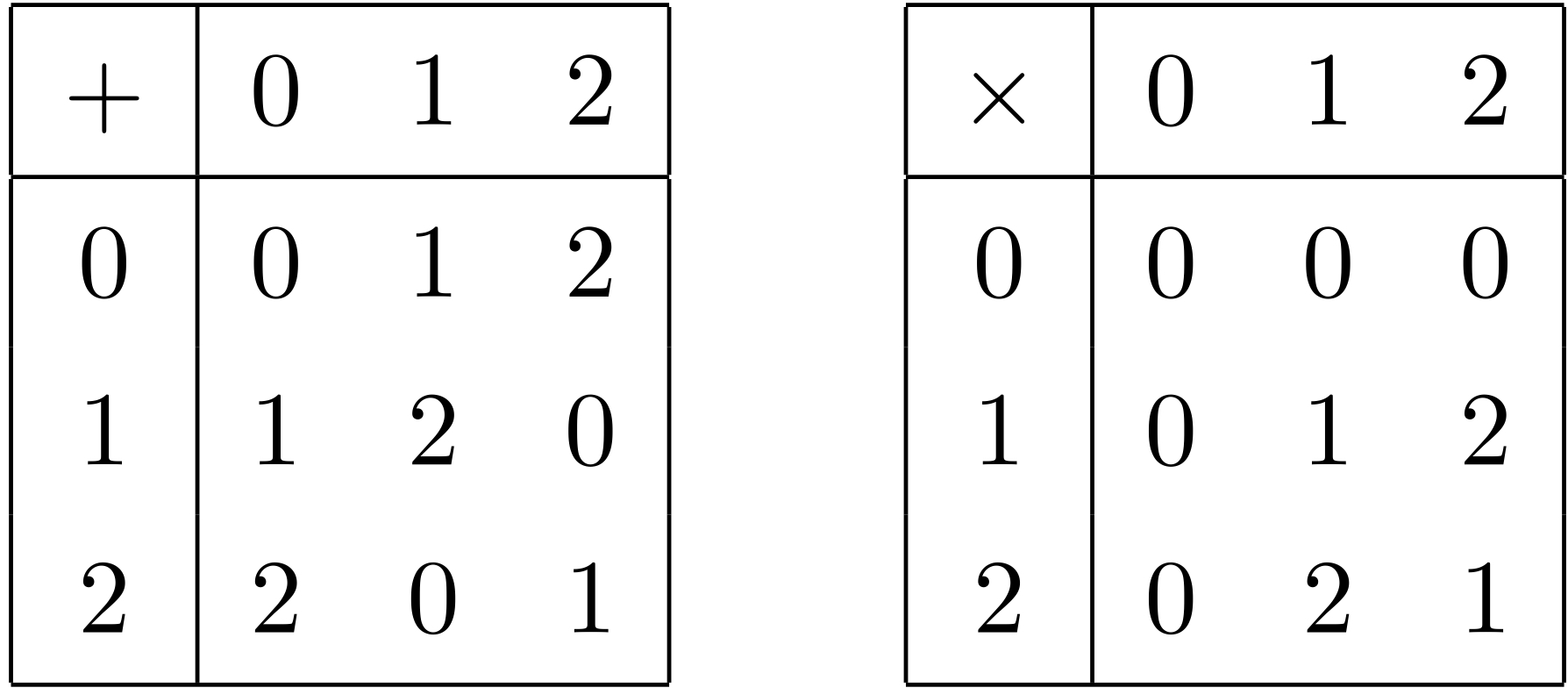
テトラ「あっ、そうでしたっ！　この演算表を使うんでしたね。 でも、 $k = -2$ としたら、すでに $k$ は $0,1,2$ のどれでもありませんよね？」

僕「いやいや。《九点平面》の世界では $-2 = 1$ だよ。 だって、 $-2$ と $1$ はどちらも $3$ で割ったときに余りが $1$ になるから。 つまり、 $$ -2 \equiv 1 \pmod{3} $$ ということ」

テトラ「ああ、そうでした。 $3$ 個進めばぐるっと回るんでしたね。トーラスです（第439回参照）。 ……ということは、 $k = -2$ は《九点平面》では $k = 1$ と同じこと。 だとしたら $k = 1$ なら、二つ目の式 $2 = 2k$ も満たします！」

僕「うん。 だから、 $k = 1$ のとき、 $$ \vAP = k\vOB $$ が成り立つ。つまり、 ベクトルを使って平行を定義したとき、 $\TT{AP}$ と $\TT{OB}$ は平行だといえる」

テトラ「ということはですよ、 四辺形 $\TT{OAPB}$ は《九点平面》の世界における《平行四辺形》といえますね！」

僕「そうだね！」

ミルカ「今日は、どんな数学？」

僕「あ、ミルカさん」

テトラ「いまは、ベクトルで《九点平面》というものを考えているところです」

ミルカ「ふうん……ところで、村木先生からテトラへの伝言がある」

テトラ「伝言？　あたしに？」

ミルカ「テトラに《カード》を渡すとき、直線とは何かと言い忘れたそうだ」

テトラ「直線とは何か……哲学的ですね」

ミルカ「哲学じゃない。数学だ」

テトラ「直線というのは、こう……何と言いますか。まっすぐな線で——」

僕「なるほど！！」

テトラ「きゃあ！」

僕「《いわば直線》も作れるよ！　《いわば平行四辺形》や《いわば平行》だけじゃない！　 さっきは、 $\TT{AP}$ と $\TT{OB}$ が平行であることをベクトルを使って定義した。 それと同じように、この《九点平面》における直線もベクトルを使って定義できるね！！」

テトラ「直線を——定義する？」

ミルカ「ふうん……直線のパラメータ表示？」

僕「そうそう！」

直線のパラメータ表示

テトラ「はあ……」

僕「通常の平面ベクトルや空間ベクトルの場合は、パラメータ $t$ は実数全体を動くんだよ。 だから、 $\vOA + t\vAP$ という式は、 《点 $\TT{O}$ から点 $\TT{A}$ に進み、 そこからさらにベクトル $\vAP$ の向きに $\vAP$ の長さの $t$ 倍だけ進んでたどり着く点》 を表している」

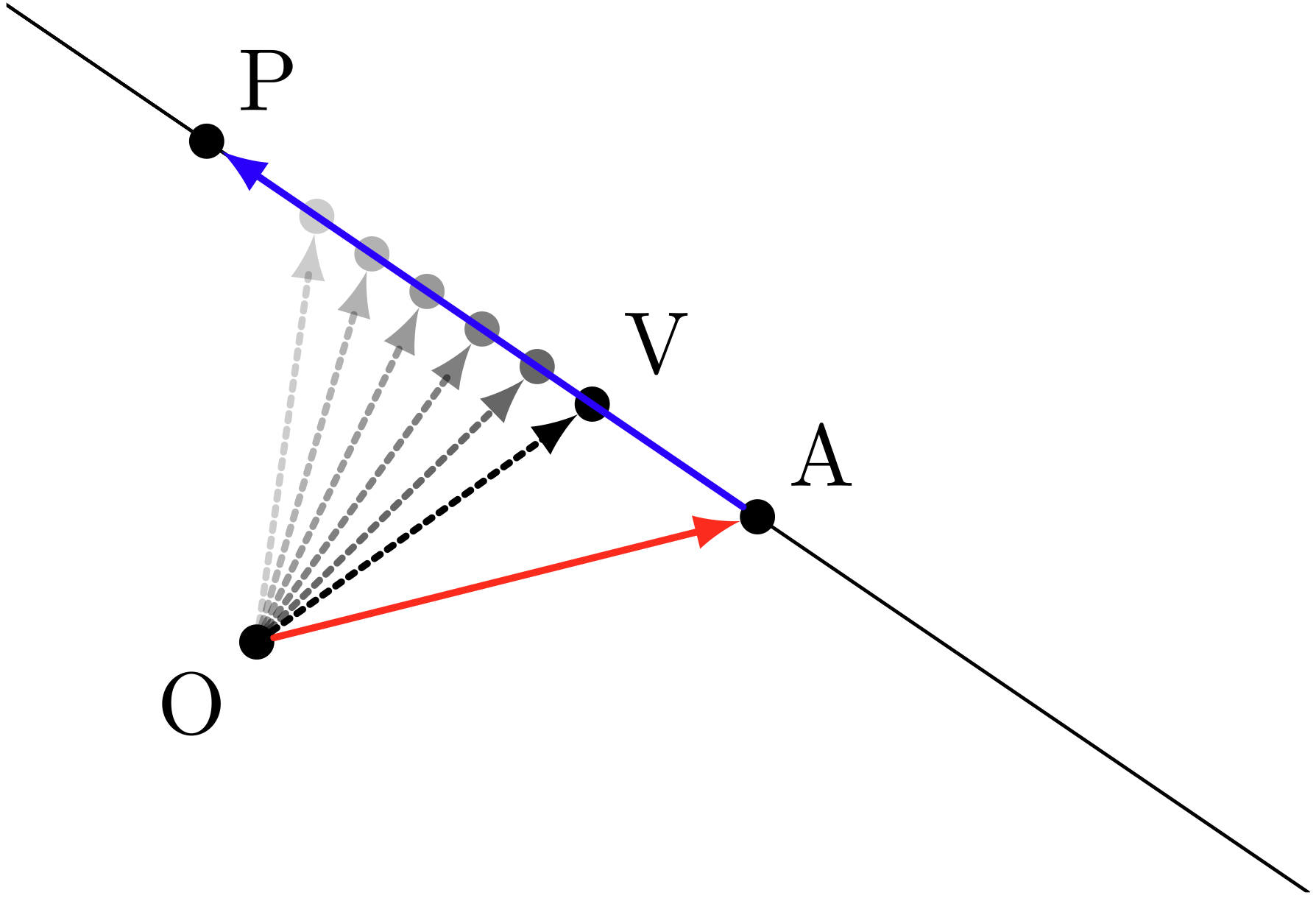
テトラ「なるほど、確かにそれは直線です……それで？」

僕「それでね、僕たちの《九点平面》においても、 この《直線のパラメータ表示》を使って直線というものを考えられるんだ。 《九点平面》にはベクトルがある。ベクトルの和もスカラー倍もある。 だから、まったく同じ定義で《いわば直線》が定義できる！」

ミルカ「《いわば直線》というか、直線そのものだな」

テトラ「あの……でも、さきほどからすでに四点 $\TT{O},\TT{A},\TT{P},\TT{B}$ を直線で結んでいましたよね。 わざわざ定義する意味がよくわかっていないようです……すみません」

僕「うん、それはそうなんだけど、ここで使っていた直線は補助的なものに過ぎないよ。 僕たちの《九点平面》にはたった九個の点しかない（・・・・・・・・・・・）と考えるなら、 点と点を結ぶ途中には何もないんだから」

テトラ「ははあ……少しわかりました。 つまり、四辺形 $\TT{OAPB}$ は、 四辺形と呼んではいるけれど、 《九点平面》では、単に四点 $\TT{O},\TT{A},\TT{P},\TT{B}$ に過ぎない、ということでしょうか」

僕「そうだね。 《九点平面》の世界では、四辺形 $\TT{OAPB}$ に《辺》というものはなくて、 $$ \TT{O},\TT{A},\TT{P},\TT{B} $$ という四つの点の集合でしかないといえるね。 つまり、 $$ \SET{\TT{O},\TT{A},\TT{P},\TT{B}} $$ という集合が四辺形 $\TT{OAPB}$ なんだよ」

ミルカ「それは違うな」

僕「え、どうして？」