$
\newcommand{\TEXT}[1]{\textbf{#1}}
\newcommand{\REMTEXT}[1]{\textbf{#1}}
\definecolor{CUD-GREEN}{rgb}{0.012,0.686,0.478}% 3,175,122
\newcommand{\MARK}[1]{\textcolor{red}{#1}}
\newcommand{\MARKA}[1]{\textcolor{red}{#1}}
\newcommand{\MARKB}[1]{\textcolor{blue}{#1}}
\newcommand{\MARKC}[1]{\textcolor{CUD-GREEN}{#1}}
\newcommand{\GEQ}{\geqq}
\newcommand{\LEQ}{\leqq}
\newcommand{\NEQ}{\neq}
\newcommand{\FOCUS}[1]{\fbox{ $#1$ }}
\newcommand{\REDFOCUS}[1]{\textcolor{red}{#1}}
\newcommand{\GREENFOCUS}[1]{\textcolor{CUD-GREEN}{#1}}
\newcommand{\BLUEFOCUS}[1]{\textcolor{blue}{#1}}
\newcommand{\BROWNFOCUS}[1]{\textcolor{brown}{#1}}
\newcommand{\REDHEART}{\REDFOCUS{\heartsuit}}
\newcommand{\REDTEXT}[1]{\textcolor{red}{#1}}
\newcommand{\GREENTEXT}[1]{\textcolor{CUD-GREEN}{#1}}
\newcommand{\BLUETEXT}[1]{\textcolor{blue}{#1}}
\newcommand{\ABS}[1]{|#1|}
\newcommand{\PHANTOMEQ}{\phantom{{}={}}}
\newcommand{\SQRT}[1]{\sqrt{#1}}
\newcommand{\PS}[1]{\left(#1\right)}
\newcommand{\SGN}{\textrm{sgn}}
\newcommand{\DOTNAME}[1]{\quad\cdots(#1)}
\newcommand{\BAR}[1]{\overline{#1}}
\newcommand{\TRIANGLE}{\triangle}
\newcommand{\TT}[1]{\textrm{#1}}
\newcommand{\TTred}[1]{\textcolor{red}{\textrm{#1}}}
\newcommand{\TTblue}[1]{\textcolor{blue}{\textrm{#1}}}
\newcommand{\ANGLE}[1]{\angle\textrm{#1}}
\newcommand{\TRI}[1]{\triangle\textrm{#1}}
\newcommand{\AP}{\TT{AP}}
\newcommand{\PB}{\TT{PB}}
\newcommand{\BQ}{\TT{BQ}}
\newcommand{\QC}{\TT{QC}}
\newcommand{\CR}{\TT{CR}}
\newcommand{\RA}{\TT{RA}}
\newcommand{\AA}{\TT{AA}}
\newcommand{\AB}{\TT{AB}}
\newcommand{\AC}{\TT{AC}}
\newcommand{\AP}{\TT{AP}}
\newcommand{\AQ}{\TT{AQ}}
\newcommand{\AR}{\TT{AR}}
\newcommand{\PQ}{\TT{PQ}}
\newcommand{\QR}{\TT{QR}}
\newcommand{\BC}{\TT{BC}}
\newcommand{\CA}{\TT{CA}}
\newcommand{\LONGVEC}[1]{\overrightarrow{#1}}
\newcommand{\vAP}{\LONGVEC{\AP}}
\newcommand{\vPB}{\LONGVEC{\PB}}
\newcommand{\vBQ}{\LONGVEC{\BQ}}
\newcommand{\vQC}{\LONGVEC{\QC}}
\newcommand{\vCR}{\LONGVEC{\CR}}
\newcommand{\vRA}{\LONGVEC{\RA}}
\newcommand{\vAA}{\LONGVEC{\AA}}
\newcommand{\vAB}{\LONGVEC{\AB}}
\newcommand{\vBC}{\LONGVEC{\BC}}
\newcommand{\vAC}{\LONGVEC{\AC}}
\newcommand{\vAP}{\LONGVEC{\AP}}
\newcommand{\vAQ}{\LONGVEC{\AQ}}
\newcommand{\vAR}{\LONGVEC{\AR}}
\newcommand{\vPQ}{\LONGVEC{\PQ}}
\newcommand{\vQR}{\LONGVEC{\QR}}
\newcommand{\avAP}{\ABS{\vAP}}
\newcommand{\avPB}{\ABS{\vPB}}
\newcommand{\avBQ}{\ABS{\vBQ}}
\newcommand{\avQC}{\ABS{\vQC}}
\newcommand{\avCR}{\ABS{\vCR}}
\newcommand{\avRA}{\ABS{\vRA}}
\newcommand{\va}{\vec{a}}
\newcommand{\vb}{\BLUEFOCUS{\vec{b}}}
\newcommand{\vc}{\REDFOCUS{\vec{c}}}
\newcommand{\vZ}{\vec{0}}
\definecolor{MUTE-COLOR}{rgb}{0.6,0.6,0.6}%
\definecolor{NOMUTE-COLOR}{rgb}{0.0,0.0,0.0}%
\definecolor{REDNOMUTE-COLOR}{rgb}{1.0,0.0,0.0}%
\newcommand{\MUTE}[1]{\textcolor{MUTE-COLOR}{\TT{#1}}}
\newcommand{\NOMUTE}[1]{\textcolor{NOMUTE-COLOR}{\TT{#1}}}
\newcommand{\REDNOMUTE}[1]{\textcolor{REDNOMUTE-COLOR}{\TT{#1}}}
\newcommand{\mvAA}{\LONGVEC{\MUTE{A}\NOMUTE{A}}}
\newcommand{\mvAB}{\LONGVEC{\MUTE{A}\NOMUTE{B}}}
\newcommand{\mvAC}{\LONGVEC{\MUTE{A}\NOMUTE{C}}}
\newcommand{\mvAP}{\LONGVEC{\MUTE{A}\NOMUTE{P}}}
\newcommand{\mvAQ}{\LONGVEC{\MUTE{A}\NOMUTE{Q}}}
\newcommand{\mvAR}{\LONGVEC{\MUTE{A}\NOMUTE{R}}}
\newcommand{\mvAV}{\LONGVEC{\MUTE{A}\NOMUTE{V}}}
\newcommand{\mvRevAB}{\LONGVEC{\REDNOMUTE{A}\NOMUTE{B}}}
\newcommand{\mvRevAC}{\LONGVEC{\REDNOMUTE{A}\NOMUTE{C}}}
\newcommand{\BP}{\TT{BP}}
\newcommand{\vBP}{\LONGVEC{\BP}}
\newcommand{\NEAREQ}{\fallingdotseq}
$
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。
僕のことを《お兄ちゃん》と呼ぶ。
論理的な話は好きだが飽きっぽい。
メネラウスの定理
メネラウスの定理
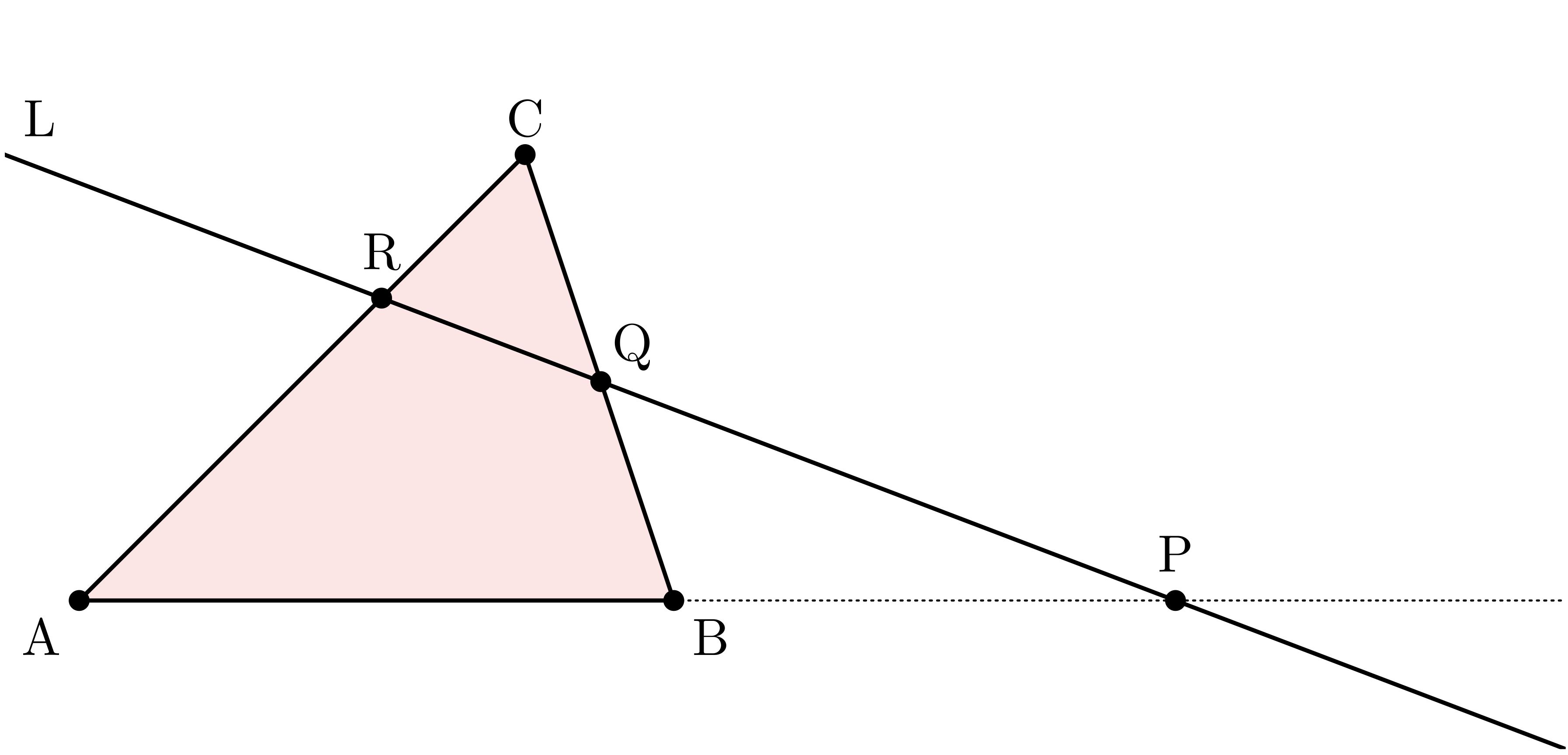
平面上に三角形 $\TT{ABC}$ がある。
また図のように、
辺 $\BC$ と辺 $\CA$ に交わる直線 $\TT{L}$ がある。
- 直線 $\AB$ と直線 $\TT{L}$ の交点を $\TT{P}$ とする。
- 辺 $\BC$ と直線 $\TT{L}$ の交点を $\TT{Q}$ とする。
- 辺 $\CA$ と直線 $\TT{L}$ の交点を $\TT{R}$ とする。
このとき、
$$
\frac{\AP}{\PB}
\times
\frac{\BQ}{\QC}
\times
\frac{\CR}{\RA}
=
1
$$
が成り立つ。
僕とユーリはメネラウスの定理に取り組み、
それぞれ違った補助線を引いて、
証明することができた(第431回参照)。
そこで僕はふと、
ベクトルを使ってメネラウスの定理が証明できるのでは、と気付いた(第432回参照)。
ユーリにベクトルの説明をしながら計算を進め、
ようやく証明までたどり着いたところ(第433回参照)。
証明できた!
僕「……ほら出た!
これで、
$\vAP = p\vPB$ と、
$\vBQ = q\vQC$ と、
$\vCR = r\vRA$ から、
$$
pqr = -1
$$
が出てきた。
ここから、
$$
\ABS{p}\times\ABS{q}\times\ABS{r} = 1
$$
がいえる。
つまりこれで、
$$
\frac{\AP}{\PB}
\times
\frac{\BQ}{\QC}
\times
\frac{\CR}{\RA}
=
1
$$
が言えたことになる。
ベクトルを使ってメネラウスの定理が証明できたんだ!」
ユーリ「はい、おめでとー」
僕「なぜ棒読み」
ユーリ「計算、疲れて飽きたんだもん。ベクトルってめんどくさいね」
僕「お疲れさま。エレガントに証明しようと考えるんじゃなくて、《腕力》でかなり泥臭く計算したからね。
ふと『ベクトルでも示せるんじゃないか』と思ってしまったからなあ……」
ユーリ「ふと思ったのが運の尽き」
僕「ところで、いま計算した結果が
$$
pqr = -1
$$
になったことで、ふと気付いたことがあるんだ」
ユーリ「またかい!」
僕「ちょっとしたことだけど……どうして、
$$
pqr = 1
$$
じゃなくて、
$$
pqr = -1
$$
になったんだろう」
$pqr < 0$ の意味を考えよう
ユーリ「えーっ! また計算し直すの? どっか間違った?」
僕「いやいや、そうじゃないよ。証明はもう終わり。
ベクトルを使ってメネラウスの定理を証明できた」
ユーリ「あーよかった」
僕「僕たちは、
$$
\begin{cases}
\vAP &= p\vPB & \REMTEXT{(ア)} \\
\vBQ &= q\vQC & \REMTEXT{(イ)} \\
\vCR &= r\vRA & \REMTEXT{(ウ)} \\
\end{cases}
$$
と置いた。
$pqr$ の結果が $1$ でも $-1$ でも、
$$
\frac{\AP}{\PB}
\times
\frac{\BQ}{\QC}
\times
\frac{\CR}{\RA}
=
1
$$
は成り立つ。
$$
\begin{align*}
\frac{\AP}{\PB}
\times
\frac{\BQ}{\QC}
\times
\frac{\CR}{\RA}
&=
\frac{\ABS{\vAP}}{\ABS{\vPB}}
\times
\frac{\ABS{\vBQ}}{\ABS{\vQC}}
\times
\frac{\ABS{\vCR}}{\ABS{\vRA}} \\
&=
\ABS{p}\times\ABS{q}\times\ABS{r} \\
&=
1
\end{align*}
$$
だから、証明はいいんだよ。
でも、どうして $pqr$ がマイナスになるのか、ちょっと気にならない?」
ユーリ「気になると言われましても」
僕「$pqr < 0$ には、何か意味があるんじゃないか——ということ」
「僕」の問いかけ
$pqr < 0$ には、何か意味があるのではないか。
そこでユーリは口を開きかけて……またすぐに口を閉じた。
本気で考えるモードに入ったらしい。

![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」

