![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
メネラウスの定理
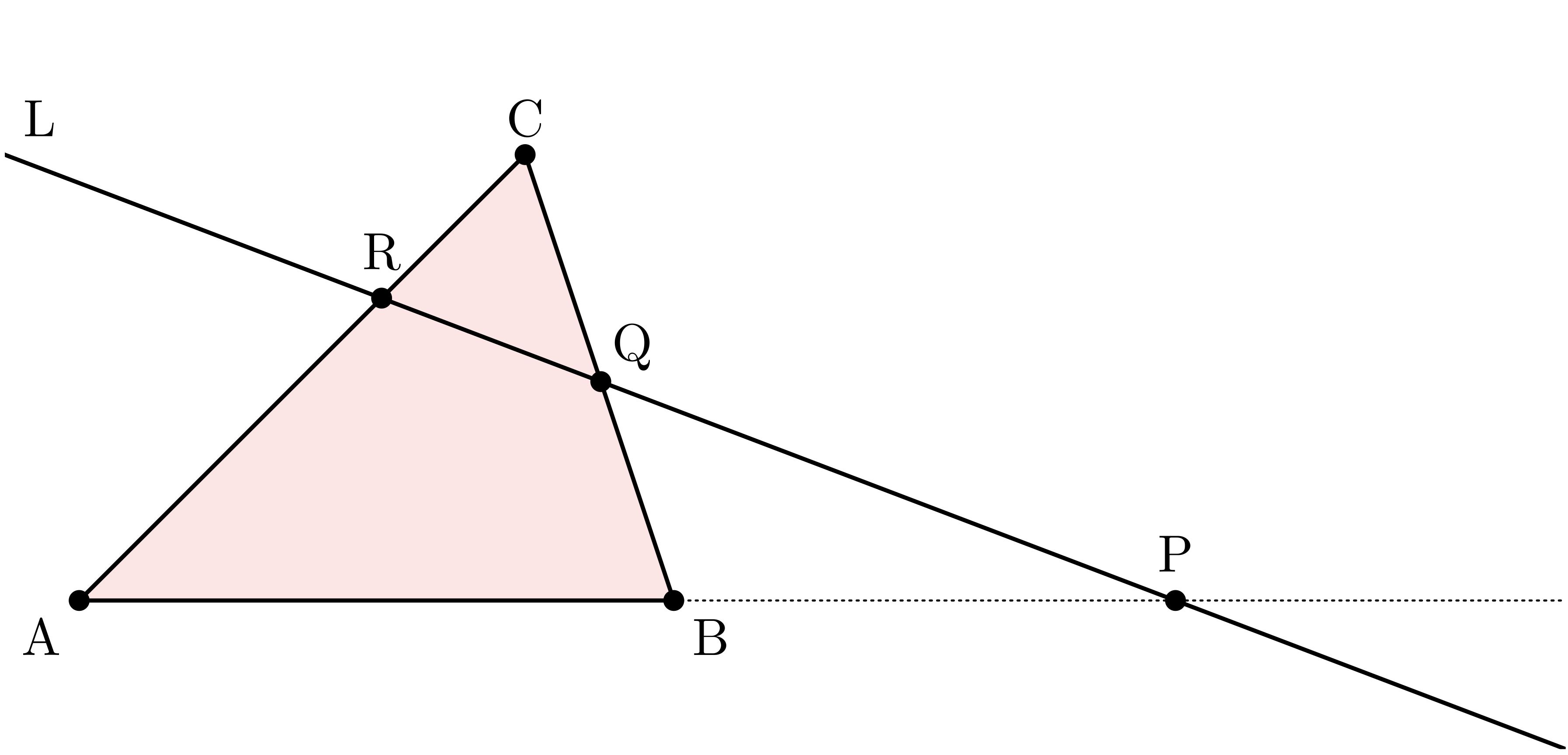
平面上に三角形 $\TT{ABC}$ がある。
また図のように、 辺 $\BC$ と辺 $\CA$ に交わる直線 $\TT{L}$ がある。
このとき、
$$ \frac{\AP}{\PB} \times \frac{\BQ}{\QC} \times \frac{\CR}{\RA} = 1 $$
が成り立つ。
僕とユーリはメネラウスの定理に取り組み、 それぞれ違った補助線を引いて、 証明することができた(第431回参照)。
そのとき僕はふと、 ベクトルを使ってメネラウスの定理が証明できる んじゃないかと思い、その計算を始めた(第432回参照)。
ステップ1(三点が一直線上にある)
僕たちは、 $p,q,r,s$ という実数を導入して、 《三点が一直線上にある》という条件を、 ベクトルを使った式(ア)(イ)(ウ)(エ)で表した。
$$ \begin{cases} \vAP &= p\vPB & \REMTEXT{(ア)} \\ \vBQ &= q\vQC & \REMTEXT{(イ)} \\ \vCR &= r\vRA & \REMTEXT{(ウ)} \\ \vPQ &= s\vQR & \REMTEXT{(エ)} \\ \end{cases} $$
ステップ2(位置ベクトル)
すべてのベクトルを $\TT{A}$ を始点に持つベクトルに書き換えた。
$$ \begin{cases} \mvAP &= p(\mvAB - \mvAP) & \REMTEXT{(ア’)} \\ \mvAQ - \mvAB &= q(\mvAC - \mvAQ) & \REMTEXT{(イ’)} \\ \mvAR - \mvAC &= r(\mvAA - \mvAR) & \REMTEXT{(ウ’)} \\ \mvAQ - \mvAP &= s(\mvAR - \mvAQ) & \REMTEXT{(エ’)} \\ \end{cases} $$
※ $\TT{A}$ が始点になっていることがはっきりするように、始点の $\TT{A}$ は色を薄くして表示しています。
ステップ3(一次独立なベクトル)
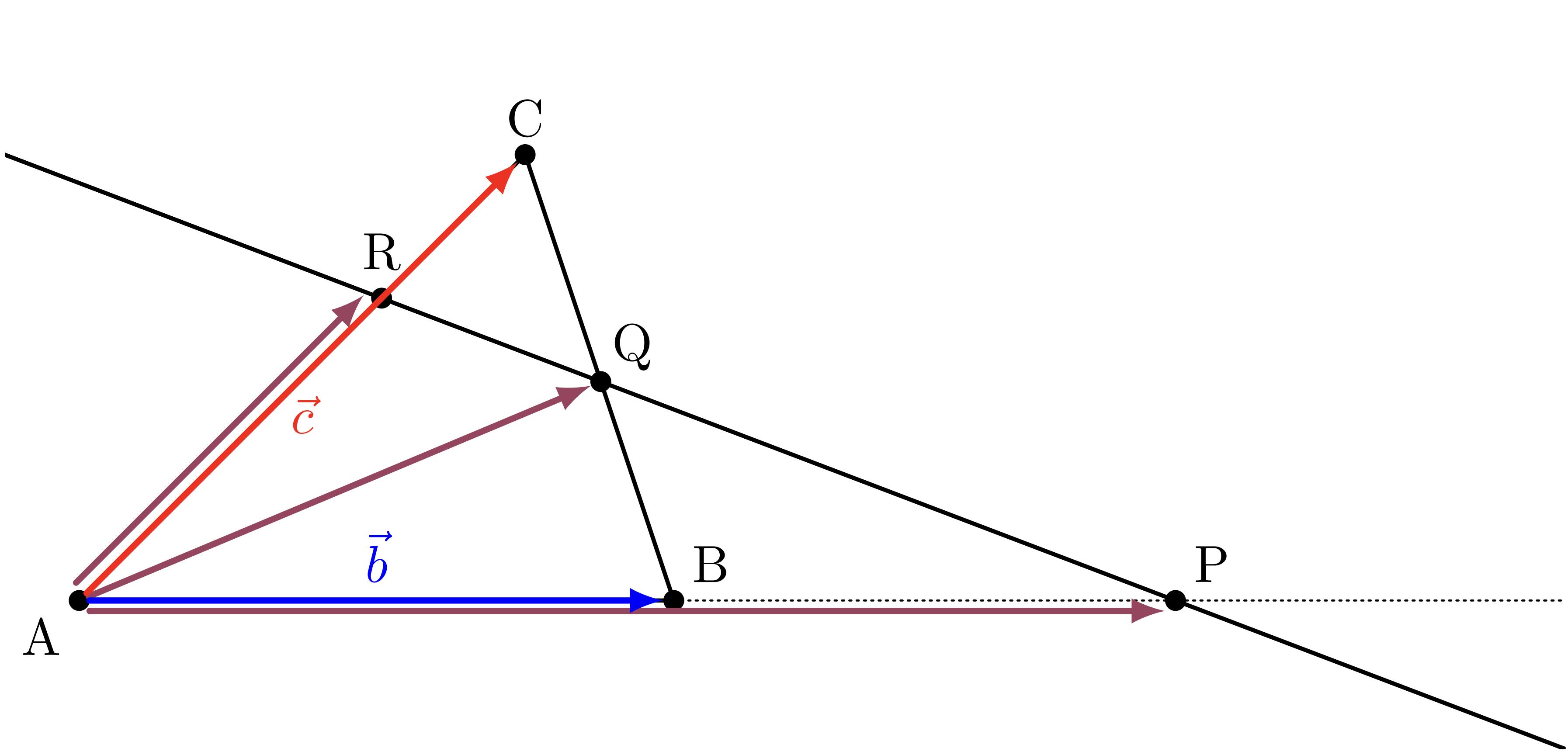
一次独立なベクトル $\mvAB$ と $\mvAC$ に注目するため、 それぞれ $\vb = \mvAB$ と $\vc = \mvAC$ に書き換えた。
\begin{cases} \mvAP &= p(\vb - \mvAP) & \REMTEXT{(ア’’)} \\ \mvAQ - \vb &= q(\vc - \mvAQ) & \REMTEXT{(イ’’)} \\ \mvAR - \vc &= r(\mvAA - \mvAR) & \REMTEXT{(ウ’’)} \\ \mvAQ - \mvAP &= s(\mvAR - \mvAQ) & \REMTEXT{(エ’’)} \\ \end{cases}
ユーリ「ここからどーすんの? どんどこ式が複雑になっていくんですけどー!」
僕「《求めるものは何か》を忘れないようにしよう」
ユーリ「もー忘れた」
僕「がく。僕たちはメネラウスの定理を証明しようとしているんだから、 $$ \frac\AP\PB\times \frac\BQ\QC\times \frac\CR\RA = 1 $$ を示したい。そのためには、 $$ \ABS{p}\times\ABS{q}\times\ABS{r} = 1 $$ を示せばいい。だから $p,q,r$ の関係が求めるものになる。 まあ、そうなるように $p,q,r$ を選んだんだけど」
ユーリ「へいへい。そーでしたな」
僕「ということは、さっきの(ア’’)(イ’’)(ウ’’)(エ’’)の式で $p,q,r$ は大事な数だ。 でも、 $s$ は消えても構わない。消えてほしいという気持ちがある」
ユーリ「にゃるほど」
僕「それから、僕たちが使える大事な《武器》は、 一次独立な $\vb$ と $\vc$ だ。この二つですべての点が表せるんだから(第432回参照)」
ユーリ「《武器》なんて、テトラさんみたいなこと言う」
僕「あはは、そうだね。……そこで、 (ア’’)(イ’’)(ウ’’)(エ’’)を $\vb$ と $\vc$ で整理してみる」
ユーリ「お兄ちゃんは、 《式を整理する》っていつもパパパッとやっちゃうよね」
僕「え? そうかなあ……今回の場合でいうと、 《$\vb$ と $\vc$ で整理する》というのは、 《$\mvAP,\mvAQ,\mvAR$ などを、 $\vb$ と $\vc$ を使って表す式を作る》という意味で言ったんだけど」
ユーリ「だったら、そー言ってほしいにゃあ……」
僕「そうだね。たとえば、(ア’’)を見ると、 $$ \mvAP = p(\vb - \mvAP) $$ という式がある。 $\mvAP$ が両辺にわかれわかれになっているので、 これを一つにまとめる」
ユーリ「まとめる……」
僕「$\vb$ や $\mvAP$ といったベクトルが、 それぞれ数を表す文字であるかのように式の計算を行って、 $$ \mvAP = \textrm{《$\vb$と$\vc$を使った式》} $$ という形にもっていくという意味だよ」
ユーリ「$\vc$ なんてないけど」
僕「(ア’’)ではそうだね。 $\vb$ だけだ。ともかく、実際にやってみよう」
ユーリ「ダウト!」
僕「何がダウト?」
ユーリ「いまさらっと $1+p$ で割ったけど、これゼロ割にならないの?」
僕「鋭いなあ……いや、大丈夫だよ」
ユーリ「理由を述べたまえ」
$\vAP = p\vPB$
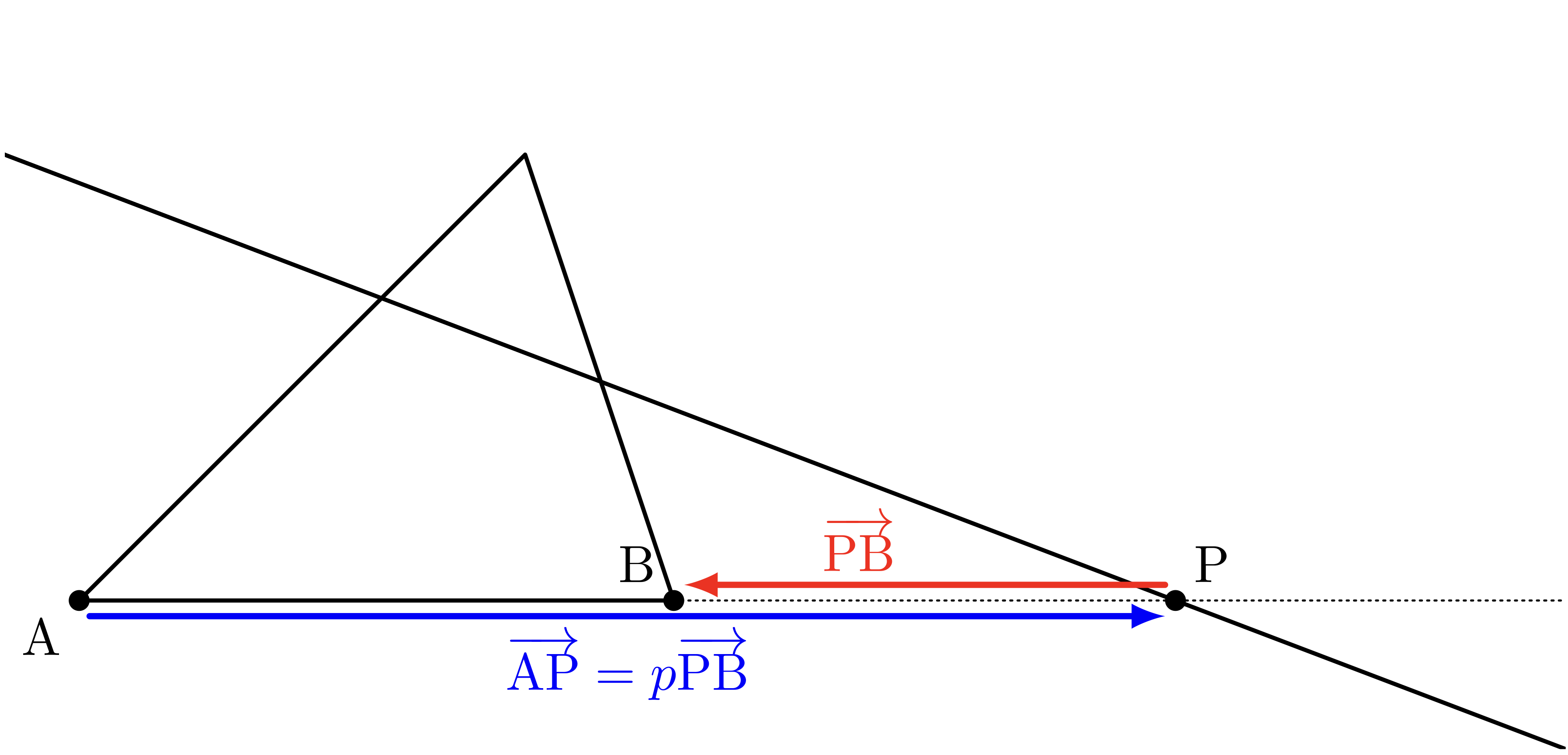
僕「$p$ という数は何だったかというと、 $$ \vAP = p\vPB $$ を満たす実数だった。 もしも $1+p = 0$ だったら、 $p = -1$ になるけど、 そうしたら、 $$ \vAP = -\vPB $$ つまり、 $$ \vAP + \vPB = \vZ $$ になる。 $\vZ$ というのは零ベクトルのこと。 零ベクトルというのは、大きさが $0$ で向きのないベクトル」
ユーリ「ぜろべくとる」
僕「要するに、始点と終点が一致しているベクトルだ。 でも、 $$ \vAP + \vPB = \vAB $$ なんだから、もし $\vAB = \vZ$ になってしまったら、点 $\TT{A}$ と点 $\TT{B}$ が一致していることになる。 でも、そんなことはありえない。 $\TT{A}$ と $\TT{B}$ は異なる二点だから。だよね?」
ユーリ「そりゃそーだ! だって $\TT{A}$ と $\TT{B}$ が同じ点なら三角形できないもん!」
僕「そういうこと。だから $1+p$ で割ってもかまわない」
ユーリ「ナットクした。それから、いまの、何だか面白かった」
僕「《いまの》?」
ユーリ「$1+p$ が $0$ じゃない理由が《三角形ができなくなるから》なのが面白かった」
僕「なるほどなあ……ユーリが感じる面白ポイントが面白いな。 そんなふうに隠れた条件が見つかることってときどきあるよ。 《三角形 $\TT{ABC}$》といったときに、 《$\TT{A},\TT{B},\TT{C}$ は異なる三点》という条件が暗黙のうちに入り込んでたりする」
ユーリ「アンモクって何」
僕「『暗黙のうちに』というのは、 『はっきりとは表されていないけど、表されたことから考えれば』ということ。 いまの場合でいうと、 $p$ を導入したときに、本当は $p$ の範囲を意識しないといけなかったんだね」
ユーリ「ふーん……」
僕「これで、(ア’’)から、 $$ \mvAP = \frac{p}{1+p}\vb $$ がわかった。さっきは $\vc$ がないって話をしてたけど、 $$ \mvAP = \frac{p}{1+p}\vb + \FOCUS{0\vc} $$ のように $\vc$ は $0$ 倍したと考えれば $\vb$ と $\vc$ で $\mvAP$ を表したことになる」
ユーリ「ほほー」
$\vAP$ を $\vb$ と $\vc$ で表した
$$ \mvAP = \frac{p}{1+p}\vb $$
僕「そして、(イ’’)(ウ’’)(エ’’)も同じように——」
ユーリ「——式を整理する」
僕「そういうこと」
僕とユーリは、同じような計算を行って、 $\mvAQ$ を $\vb$ と $\vc$ で表した。
$\mvAQ$ を $\vb$ と $\vc$ で表した
$$ \mvAQ = \frac{1}{1+q}\vb + \frac{q}{1+q}\vc $$
ユーリ「慣れてきた。確かに《式の計算》だね、これ」
僕「(ウ’’)の式には、 $\mvAA$ が出てくるけど、これは $\vZ$ だね」
ユーリ「零ベクトル。始点と終点が同じだから」
僕「そう。 $\mvAA$ は点 $\TT{A}$ から点 $\TT{A}$ へ向かうベクトルだから、大きさが $0$ で向きがない零ベクトル。 $\vZ$ は数の $0$ とそっくりだ。 どんな実数 $a$ に $0$ を足しても変わらないし、どんな実数 $a$ を $0$ に掛けても $0$ のまま。 $$ a + 0 = a, \qquad a\times 0 = 0 $$ それと同じように、 どんなベクトル $\vec{v}$ に $\vZ$ を足しても変わらないし、どんな実数 $a$ を $\vZ$ に掛けても $\vZ$ のまま。 $$ \vec{v} + \vZ = \vec{v},\qquad a\vZ = \vZ $$ そんなふうに似ている」
ユーリ「ふむふむ」
$$ \begin{align*} \mvAR - \vc &= r(\mvAA - \mvAR) && \REMTEXT{(ウ’’)より} \\ \mvAR - \vc &= r(\vZ - \mvAR) && \REMTEXT{$\mvAA$は零ベクトル} \\ \mvAR - \vc &= r(- \mvAR) && \REMTEXT{零ベクトルは消える} \\ \mvAR - \vc &= -r\mvAR && \REMTEXT{展開した} \\ \mvAR + r\mvAR &= \vc && \REMTEXT{移項した} \\ (1+r)\mvAR &= \vc && \REMTEXT{$\mvAR$でくくった} \\ \mvAR &= \frac{1}{1+r}\vc && \REMTEXT{$1+r$で割った} \end{align*} $$$\mvAR$ を $\vc$ で表した
$$ \mvAR = \frac{1}{1+r}\vc $$
僕「ここまでで $\mvAP,\mvAQ,\mvAR$ を $\vb$ と $\vc$ で表したことになる」
$\mvAP,\mvAQ,\mvAR$ を $\vb$ と $\vc$ で表した
$$ \left\{ \begin{array}{rllllll} \mvAP &= \dfrac{p}{1+p}\vb & & \\ \mvAQ &= \dfrac{1}{1+q}\vb &+ & \dfrac{q}{1+q}\vc \\ \mvAR &= & & \dfrac{1}{1+r}\vc \\ \end{array} \right. $$
ユーリ「……」
僕「何か気になる?」
ユーリ「んー……ま、いいや。 お兄ちゃん、まだ(エ’’)が残ってるよ。これも同じことするんでしょ?」
$$ \mvAQ - \mvAP = s(\mvAR - \mvAQ) \qquad \REMTEXT{(エ’’)} $$僕「そうなんだけど、一本の式に $\mvAP,\mvAQ,\mvAR$ が入っているから、さっきまでとはちょっと違うね。 まずは式を整理してみよう」
ユーリ「また式の整理って言ってる」
僕「少なくとも両辺に散らばっている $\mvAQ$ をまとめてから考えたいんだよ」
$$ \begin{align*} \mvAQ - \mvAP &= s(\mvAR - \mvAQ) && \REMTEXT{(エ’’)より} \\ \mvAQ - \mvAP &= s\mvAR - s\mvAQ && \REMTEXT{展開した} \\ \mvAQ + s\mvAQ &= \mvAP + s\mvAR && \REMTEXT{移項した} \\ (1+s)\mvAQ &= \mvAP + s\mvAR && \REMTEXT{$\mvAQ$でくくった} \end{align*} $$ユーリ「そんで、両辺を $1+s$ で割って、 $\mvAQ = \cdots$」
僕「いや、ちょっと待って。そうじゃなくて、 こんなふうに $\mvAP,\mvAQ,\mvAR$ を全部、左辺に寄せてみる。 右辺は零ベクトルになる」
$$ \mvAP - (1+s)\mvAQ + s\mvAR = \vZ \qquad\cdots\cdots \heartsuit $$ユーリ「?」
僕「うん、これで行けるよ」
ユーリ「何が?」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2024年9月27日)