第420回 シーズン42 エピソード10

距離空間の定義（後編）

図書室にて

僕「……これで距離空間が定義できたんだね、テトラ先生！」

テトラ「はい……ここであたしの疑問をスタックから$\textrm{POP}$させてください」

僕「ああ、そうだったね。条件（２）？」

テトラ「そうです。あたし、この条件（２）がどうも納得いかないんです……」

僕「たとえば、イメージ図にすればこういうことだよね」

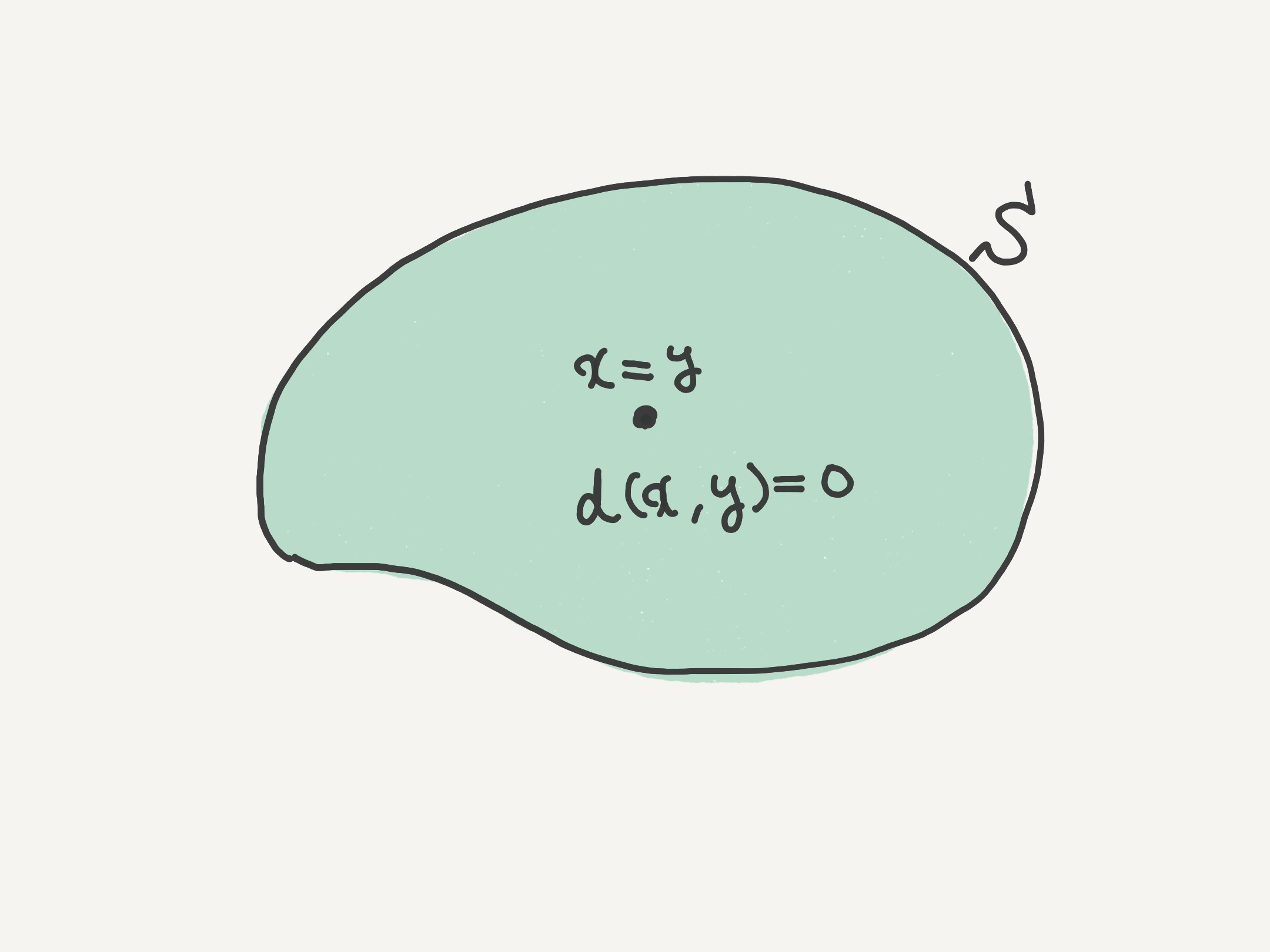
ミルカ「テトラは『納得いかない』を言語化する」

テトラ「はい……あのですね。 $S$ に属している二つの点 $x,y$ が等しいとき、つまり $x = y$ のときに距離が $0$ というのは、 特に疑問に思いません。 だって、一つの点なんですから。それはいいんです。 でも……その逆が引っかかるんです」

僕「逆は『$d(x,y) = 0$ ならば $x = y$』だね？」

ミルカ「いまはテトラが説明中」

僕「おっと、ごめん」

テトラ「はい。 $d(x,y) = 0$ のとき——この《お気持ち》は $x$ と $y$ の距離が $0$ ということですが——そのとき、 $x$ と $y$ が等しいというところが引っかかります」

ミルカ「その理由」

テトラ「引っかかる理由は、 二点 $x,y$ の距離が $0$ であっても $x \NEQ y$ で構わないのではないかしらん……と思うからです」

ミルカ「さらにその理由」

テトラ「さらにその理由……は、はい。 あたしは、距離空間を考えるとき、空中を飛び回るボールのようなものをイメージしていました。 $S$ の要素を《空中を飛び回っているボール》のように考えて、 $d(x,y)$ を《二つのボール $x$ と $y$ の距離》のように考えて、 それで、 $d(x,y) = 0$ ならば、その二つのボールが衝突するイメージで考えました」

僕「なるほど」

ミルカ「ふうん……」

テトラ「でも、二つのボールが衝突したとしても、 二つのボールは違うボールです。 違うボールが、たまたま同じ位置にあるだけです。 それなのに $d(x,y) = 0$ のとき $x = y$ としていいものかどうか……そこが引っかかっていたんです」

ミルカ「君が答える」

僕「距離空間は四つの条件で規定されていて、 その条件の一つに『$d(x,y) = 0$ は $x = y$ と同値』がある。 関数 $d$ はその条件を満たすときに距離関数になるとしたんだから、 そこで引っかかるのは不適切じゃないのかな……違う？　つまり $(S,d)$ を距離空間と呼ぶならば、 $x,y$ が $S$ の要素で、 $d(x,y) = 0$ のとき $x = y$ にならざるを得ないよね」

テトラ「……」

ミルカ「君の答えは正しいが、テトラの疑問解決にはなっていない」

僕「うーん……そうなのかな」

ミルカ「テトラは、 $d(x,y) = 0$ のとき $x = y$ になることそのもの（・・・・）に疑問を抱いているのではない。 テトラは、自分のイメージしている距離というものとの解釈のズレに疑問を抱いているのだ」

テトラ「……はい。ミルカさんがおっしゃる通りです。解釈のズレ、 まさにそうです。 日常生活に対応付けること自体がまちがっているのかもしれませんけれど……」

ミルカ「テトラは $S$ の要素を動き回るボールに見立てた。その見立て——すなわち解釈——にズレがある。 空中を飛び回るボールを考えたいのなら、 $S$ の要素はボールではなく空中の位置を表すと考えた方がいいだろうな」

テトラ「位置……？」

ミルカ「そう」

テトラ「ははあ……理解しました。 $S$ の要素をボールだと考えるのではなく、ボールの位置だと考える。 二つのボールの距離が $0$ になるというのは、 二つのボールが同じ位置に来るということになって、 $x = y$ です。 ボールは違うけれど、ボールの位置が同じ。 なるほど！」

僕「なるほどね。解釈ってそういうことか」

ミルカ「時間に応じて移動する特定のボールを考えるときには、 時刻 $t$ から $S$ の要素——つまり位置——を得る関数を考えればいい。 ボール $A$ の運動は $a(t)$ で表し、ボール $B$ の運動は $b(t)$ で表し、 $a(t)$ と $b(t)$ はどちらも $S$ の要素とすると、 $a(t) = b(t)$ が成り立つ $t$ は、二つのボール $A,B$ が衝突する時刻ということになる」

テトラ「確かに！」

僕「その場合の $S$ は三次元空間 $\REAL^3$ ということになるね」

ミルカ「そう考えてもいいけれど、そう考えなければならない理由はない。 たとえば $S$ を座標平面の格子点全体の集合と考えることも可能だ。 せっかく距離空間として抽象化したのだから、自由に考えられるということを意識した方が楽しい」

僕「そうか！　《格子点の世界》で移動する《ボール》 を考えてもいいわけだね！　そうすれば《ボールの衝突》という概念も別世界に移すことができる！」

ミルカ「そういうこと」

テトラ「なるほどです……」

ミルカ「せっかく距離空間が定義できたのだから、 日常生活では《距離》と思えない距離を考えることにしよう」

テトラ「？」

ミルカ「たとえば、ビットパターン間の距離。ハミング距離を考えよう」

ハミング距離

テトラ「ハミング距離……何だか歌が出てきそうです」

ミルカ「鼻歌のハミング（humming）ではない。数学者のハミング（Hamming）に由来する距離だ」

テトラ「ああ、ハミングさんなのですね」

ミルカ「一般の文字列で定義できるが、簡単のために $7$ ビットからなるビットパターンで説明する。 $7$ ビットからなるビットパターン全体の集合を $S$ とする。 そして $S$ の二つの要素 $x,y$ ——つまり二つのビットパターン $x,y$ を比べて《異なるビットの個数》を $d(x,y)$ とする。 すると、 $(S,d)$ は距離空間の条件を満たす」

僕「たとえば、 $0000111$ と $0010110$ の距離は $2$ ということ？」

テトラ「えっえっ？」

僕「こんなふうにビットパターンを比較するという意味だよね？　《異なるビットの個数》が $2$ 個だから」

テトラ「意味はわかりましたが……確かにこれはあまり《距離》という感じはしませんね」

僕「でも、距離空間の四つの条件は満たすよね」

テトラ「確かに、ハミング距離は距離空間の条件を満たしますが……でも、 So what?（だから、何？）という感じがします」

ミルカ「そう？」

僕「いや、でも、実際的な意味を持たないこういうものも、 定義の理解には大事なんじゃないのかな」

ミルカ「ハミング距離は実際的な応用もある」

僕「そうなんだ」

ミルカ「ちょうどいいところに」

リサ「話題？」

ミルカ「ハミング距離の応用」

リサ「ハミング符号」

ミルカ「$7$ ビットで」

リサ「データ $4$ ビットに、パリティ $3$ ビット（咳）」

ミルカ「エラーコレクション」

リサ「$1$ ビット」

ハミング符号

リサ「概要」

テトラ「通信エラーを訂正できる……間違っても正しくもとに戻せるということでしょうか？」

僕「そうみたいだね」