第408回 シーズン41 エピソード8

納得という名の宝物（後編）

僕の家

僕「たとえば、 $x$ がどんな実数でも、 $$ x^2 + 2x + 1 = (x + 1)^2 $$ は成り立つ。ここで右辺に注目してみよう。 $x$ が実数だとすると、 $$ (x + 1)^2 $$ という式を見た瞬間に『あ、この式の値は $0$ 以上になる！』とわかる。 つまり、 $x$ がどんな実数でも、 $$ (x + 1)^2 \GEQ 0 $$ という不等式が成り立つ。このことはわかる？」

ユーリ「わかるわかる」

ノナ「……」

僕「ユーリはわかった。ノナちゃんはわからない？」

ノナ「……」

僕「わからないときは、『わからない』と言ってもいいんだよ。誰も怒らないし、 時間はたっぷりあるんだから」

ノナ「わかる……わかります $\NONAX$」

僕「なるほど。『どんな実数 $x$ に対しても、 $(x + 1)^2 \GEQ 0$ という不等式が成り立つ』と言われたとき、 ノナちゃんはわかる。でも、何か気に掛かるところがあるんじゃない？　ノナちゃんのその気持ちを言葉にしたら、 どうなるだろう。試しにやってみようか」

ノナ「……」

ノナ「すぐにはわからない $\NONAX$」

僕「ああ、そうか。 $(x + 1)^2$ を見た瞬間にはわからないけれど、 ゆっくり考えればわかるって言いたいんだね」

ノナ「はい $\NONA$」

僕「なるほど、なるほど。うん、これは僕の言い方がよくなかったね。 でも慣れてきたら $(x + 1)^2$ を見るとすぐにこれは $0$ 以上だなと気付くようになるよ」

ユーリ「どっちにしても $0$ 以上だからでしょ？」

ノナ「どっち $\NONAQ$」

僕「ユーリが言いたいのは、 $x + 1$ の部分がマイナスでも、ゼロでも、プラスでも、どれにしても $2$ 乗した $(x + 1)^2$ は $0$ 以上になるってことだね」

ユーリ「そーそー！」

ノナ「大丈夫……大丈夫です $\NONA$」

僕「ちょっとだけ補足すると、 実数というのは必ず、マイナスか、ゼロか、プラスのいずれかになる。必ずそうなる。 実数は数直線上に並んでいる数だから」

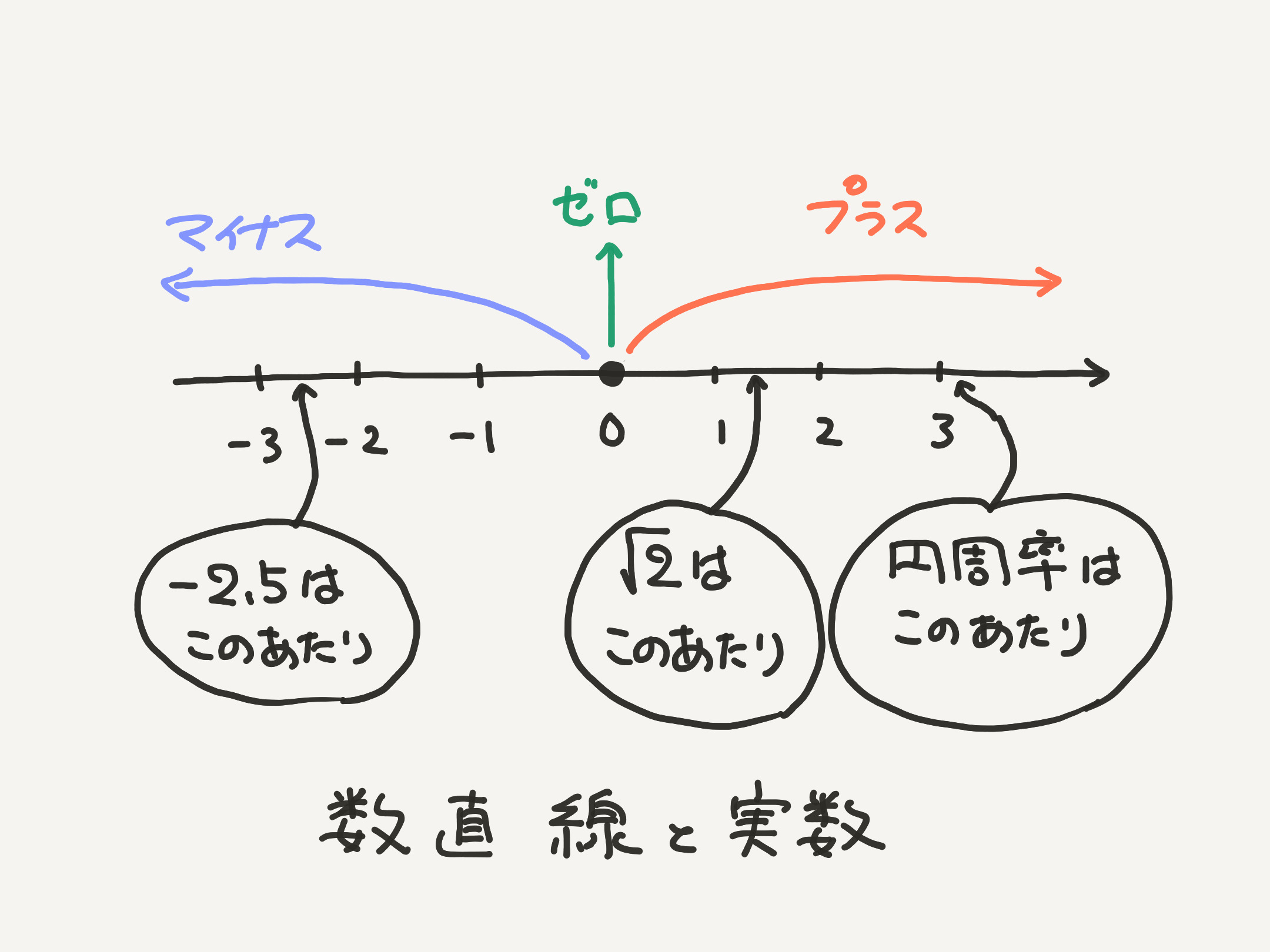
僕「そして、マイナス×マイナスはプラスになるし、ゼロ×ゼロはゼロになるし、 プラス×プラスはプラスだから、結局、実数を $2$ 乗したら必ずプラスまたはゼロになる。 プラスまたはゼロになるというのは、 $0$ 以上になるということ」

ユーリ「ずいぶん長い『ちょっとだけ補足』だにゃ（・・）」

僕「それで、ええと、話を戻すね。 僕がいいたかったのは式の書き方の話だった。 いま、 $x$ が一つの実数だとする。実数というのは数直線上にある数で、プラスかもしれないし、マイナスかもしれないし、 ゼロかもしれない。だから、 $$ x^2 + 2x + 1 $$ という式を見たときに『この式の値は絶対にマイナスにならない！』とすぐにはわからない」

ノナ「……」

僕「$x^2 + 2x + 1$ で、 $x^2$ の部分はマイナスにはならないし、 $1$ の部分はもちろんプラス。 でも、 $2x$ の部分はプラスかもしれないしマイナスかもしれない。それは $x$ がどんな実数かによる。 そうすると、 $x^2$ と $2x$ と $1$ をぜんぶ足したときに『絶対にマイナスにはならないぞ！』とはなかなか判断できない」

ノナ「そう $\NONAEX$ 　そう $\NONAEX$」

ユーリ「うおっと！」

僕「うわっ！」