![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
ユーリ「ねーお兄ちゃん、この図で並進運動しない条件は $F_1 + F_2 - F_3 = 0$ って言ったよね?」
静止している棒が並進運動しない条件
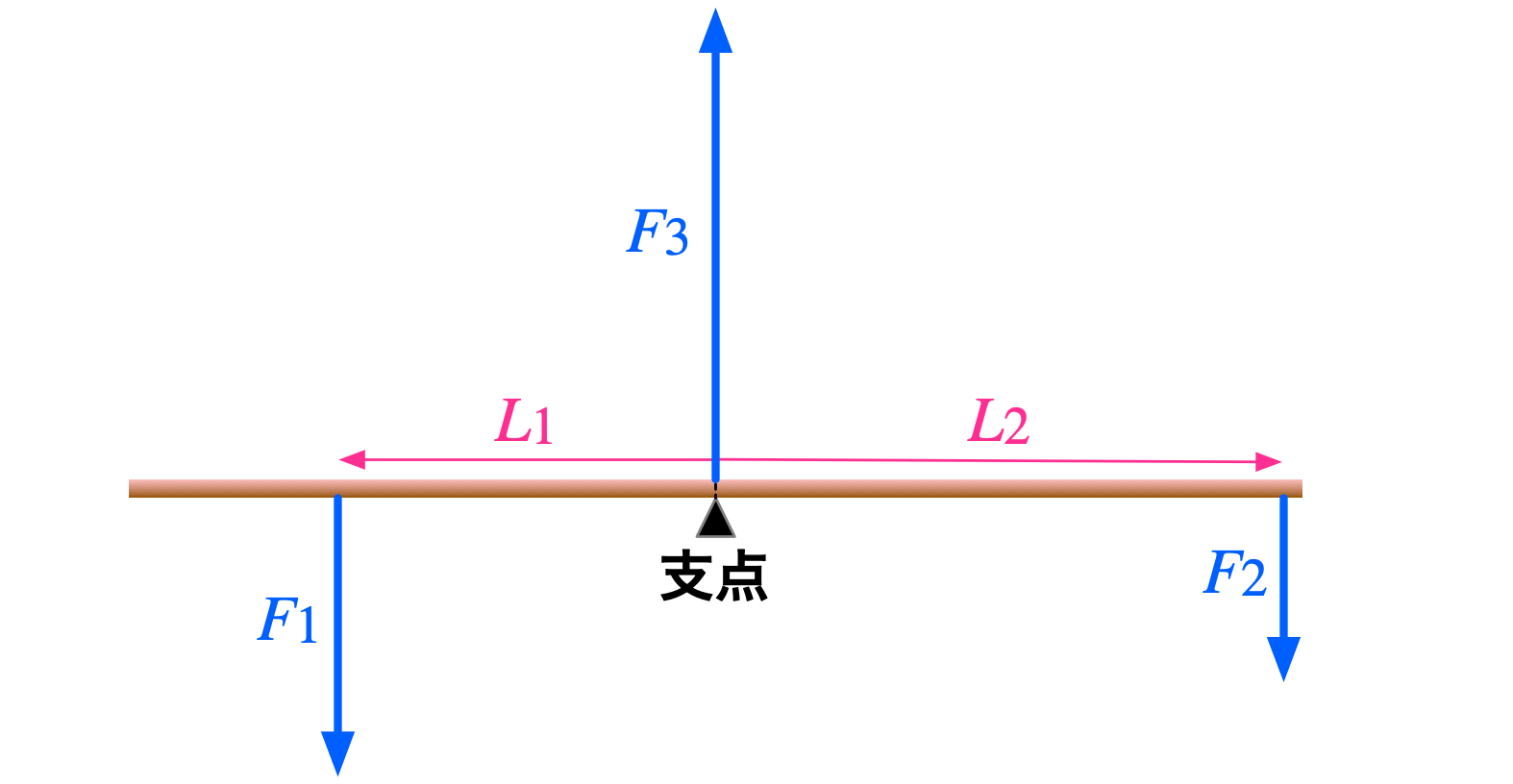
$$ F_1 + F_2 - F_3 = 0 $$
僕「そうだね。 式の中で $F_3$ にマイナスが付いているのは、向きが逆だから。 それから一般には、ベクトルの和として考える必要があるけれど——」
ユーリ「それそれ! ベクトルの和って、こーゆーんじゃなかったっけ?」
ベクトルの和

僕「うん、そうだよ。 ベクトルを矢印で表すなら、 二つのベクトル $\vec a$ と $\vec b$ の始点を合わせて角を作り、そこから平行四辺形を作ると、その対角線を使ってベクトルの和 $\vec a + \vec b$ が作れる」
ユーリ「でもお兄ちゃん、さっき、最初から平行な力 $F_1$ と $F_2$ を足し算したよね。 平行なベクトルで角はできないから、足せないのでは?」
僕「おっと! ユーリは鋭いなあ……うん、それはね、剛体に働く力について順を追って話す必要がある」
ユーリ「剛体に働く力——それって、めんどくさい話?」
僕「いや、めんどくさくはないよ」
ユーリ「ならかまわんよ。話したまえ」
僕「偉そうだな……」
ユーリ「苦しゅーない。語りたまえ」
僕「剛体に働く力を考えるときには、三つのことを考える必要がある。剛体に働く力の三要素というけど、このうち二つはわかるよね」
ユーリ「《向き》と《大きさ》でしょ。力には向きと大きさがあるから」
僕「その通り!」
ユーリ「《向き》と《大きさ》と、もう一つあるの? 何だろな……あっ、待って! わかるような気がする!」
僕「それはすごい」
ユーリ「質点は大きさがなくて、剛体は大きさがある。だから、剛体のどこに力が働くかってことじゃない? だから、力が働く位置だ! そーでしょ?」
僕「ユーリは賢いなあ! それはかなり正解に近い。というかほとんど正解だね」
ユーリ「むむ? 大正解じゃなくて、ほとんど正解?」
僕「剛体に働く力の三要素は、《向き》と《大きさ》と《作用線》になる。この三つが決まれば、その力が剛体に及ぼす影響が決まる。 この三つを決めなくては、剛体に及ぼす影響は決まらない」
ユーリ「さようせん……って何じゃ?」
僕「剛体に、こんなふうに力が働いているとする。そのとき、力が働いている点を通って、力と向きが一致する直線が作用線になる」
剛体に働く力の作用線
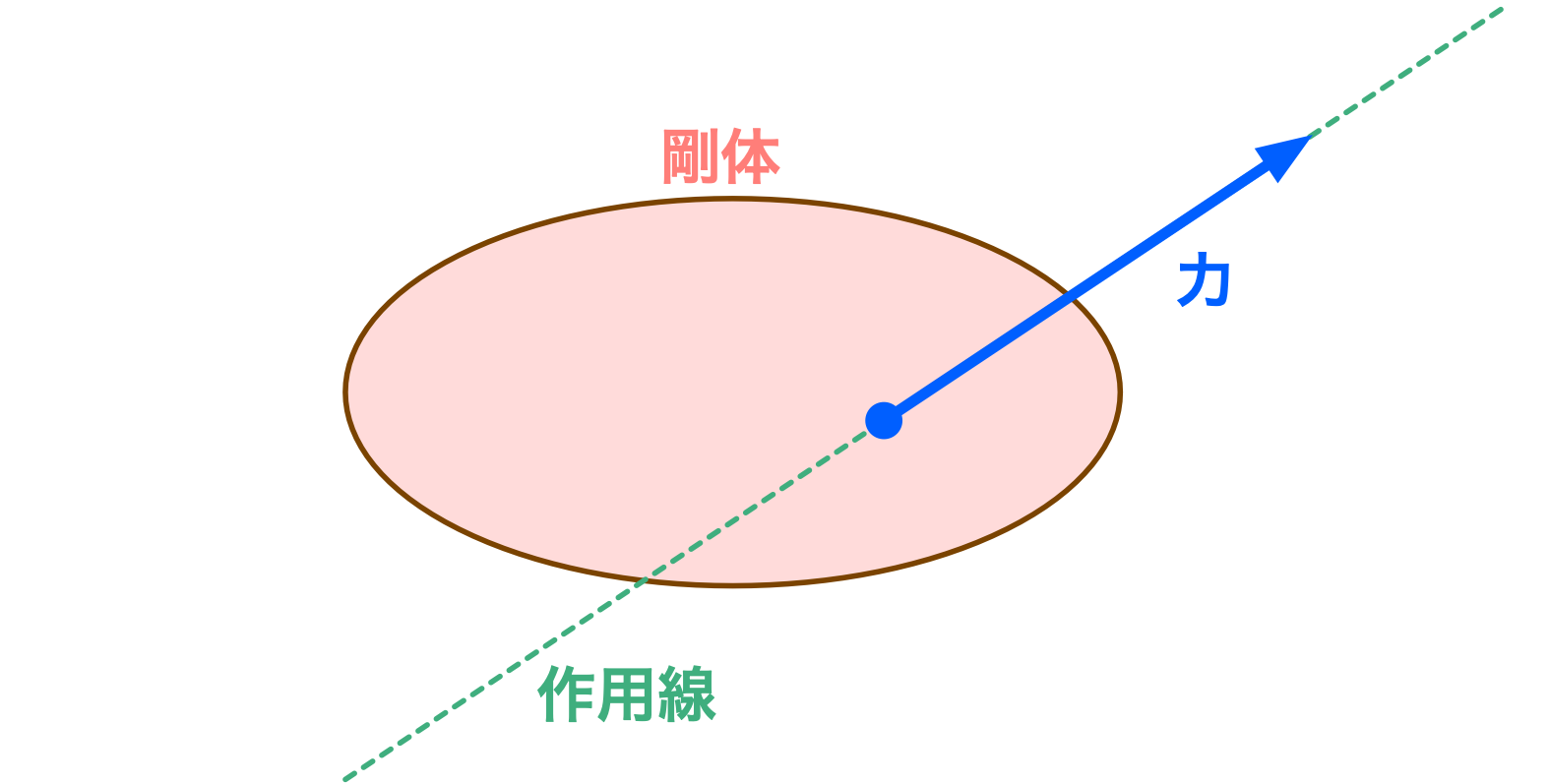
ユーリ「ふーん……それで?」
僕「力が剛体に働くとき、その影響や効果は《向き》と《大きさ》と《作用線》で決まる。 《作用線》はユーリがさっき言ったように、剛体のどこに力が働くか。力が働く位置に相当するもの」
ユーリ「えっ? 違うもん。ユーリは、剛体のどこか一点に力が掛かるって話をしてたんだもん。 だって、剛体の端っこを引っ張るのと、真ん中へんを引っ張るのは違うでしょ? 作用線は直線だから一点じゃないよ」
僕「そうだね。その通り。だから僕はユーリの答えをほとんど正解って言ったんだ」
ユーリ「うーん?」
僕「《向き》と《大きさ》と《作用線》という三つが同じ力は、剛体に対して同じ効果を及ぼす。 別の言い方をすれば、力は《作用線》上を自由にスライドさせても、剛体に対する効果はまったく同じ。 自由にスライドさせてかまわない。 剛体に働く力にはそういう性質があるんだ」
力は《作用線》上をスライドさせてもかまわない

ユーリ「信じらんない」
僕「じゃあ、これはどうかな。剛体に対して、二つの力が働いているとする。 《向き》が逆で、《大きさ》が等しくて、《作用線》が一致している。このとき、この二つの力はお互いに打ち消しあって、何も力が掛かってないことになる。 これは納得できる?」
《向き》が逆で、《大きさ》が等しくて、《作用線》が一致している二つの力は打ち消しあう
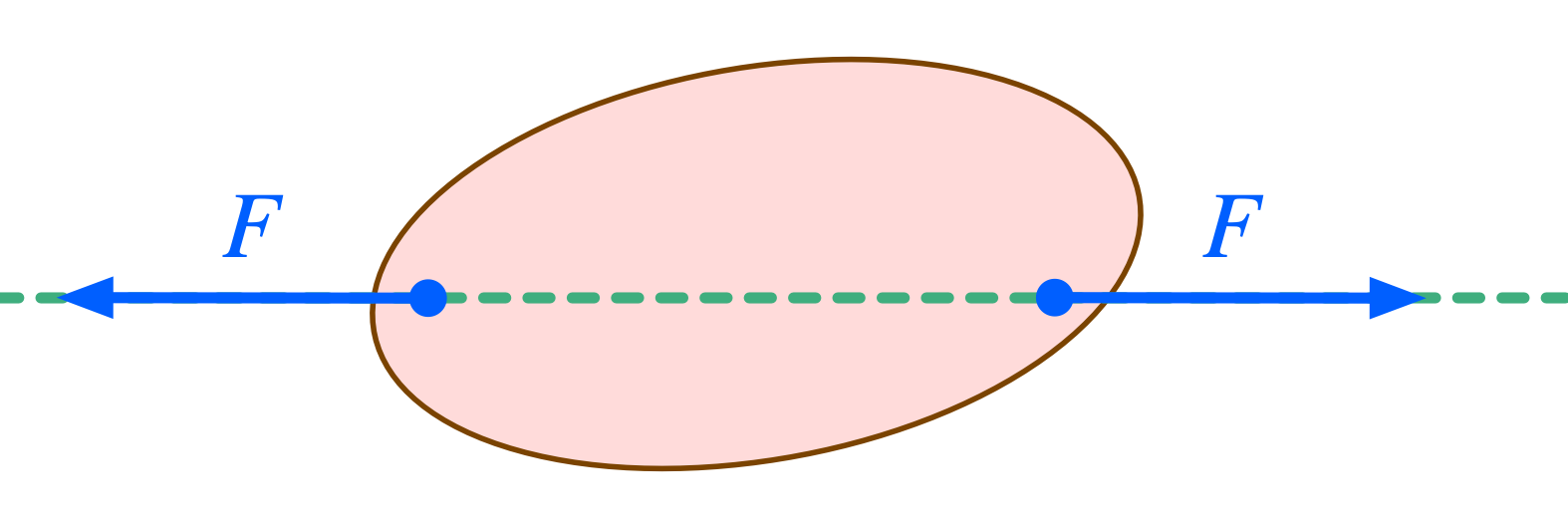
ユーリ「わかる。ナットク。力が掛かってないのと同じで、何も起きない」
僕「これが納得できるなら、剛体に働く力が《作用線》上を自由にスライドしても効果が変わらないのも納得できるよ」
ユーリ「えーっ何で? 似てるけど、違う話じゃん?」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2022年11月11日)