![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。 好奇心旺盛で根気強い《元気少女》。言葉が大好き。
テトラちゃんが村木先生からプレゼントされた《カード》にはひとつの曲線を描く手順が書かれていた(第367回参照)。
僕とテトラちゃんはそれがどんな曲線なのかを探っている。 そしてそこに隠されていた謎にようやく気付いたところ。
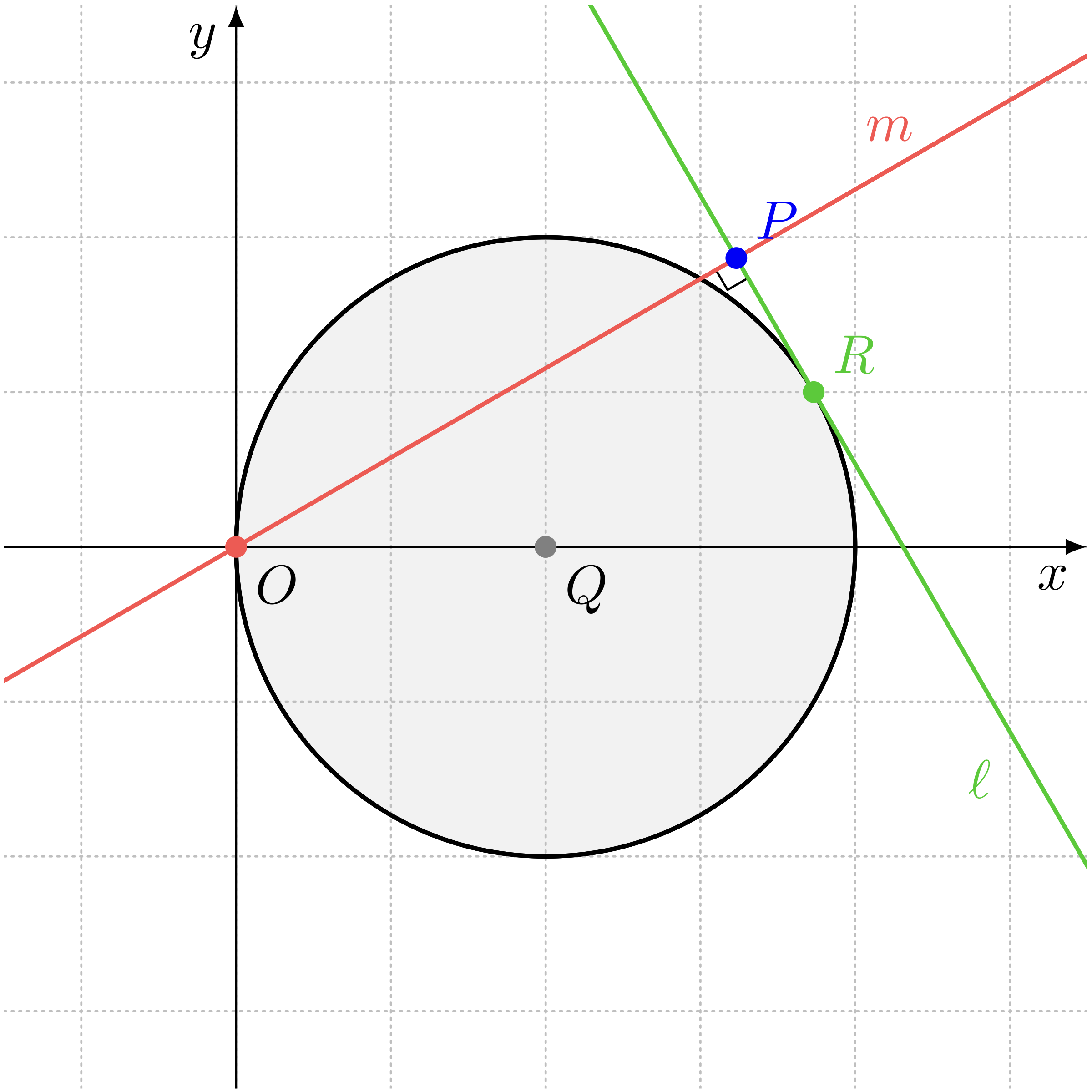
村木先生からの《カード》(第367回参照)(再掲)
以下の手順で点 $P$ を定めます。
まず、中心が点 $Q(2, 0)$ で、半径が $2$ の円 $Q$ を固定します。
次に、円 $Q$ 上の一点 $R$ を接点とする円 $Q$ の接線 $\ell$ を引きます。
ここで、原点 $O(0, 0)$ から接線 $\ell$ に対して垂線 $m$ を引いたとき、 二直線 $\ell$ と $m$ の交点を $P$ とします。
点 $R$ が円 $Q$ 上を一周するとき、点 $P$ が描く曲線 $C$ について考察してください。
僕「ねえ、テトラちゃん……村木先生からやってきた《カード》だけど、 ここに書かれた手順で生まれる曲線 $C$ というのは、 実はカージオイドなんじゃないのかな?!」
テトラ「カージオイド!? ……でも、そんなこと、あるんでしょうか? だって、 カージオイドは、円板のまわりを別の円板が転がるときに生まれる曲線ですよね? でもこの曲線 $C$ は、それとはぜんぜん違う作り方をしてますよ!」
僕「いやいや、《違う作り方》から《同じ曲線》が生まれることはあるよね」
テトラ「そう……ですか?」
僕「もっとも、この曲線 $C$ が本当にカージオイドなのかはまだわからないよ。 見た目から、そうだと予想しただけだから。証明できなければ、予想は予想に過ぎない」
テトラ「証明——証明する? この曲線 $C$ がカージオイドであることを証明する?!」
僕「そうだね。どうやら僕たちは、村木先生の《カード》の謎をやっと見つけたみたいだよ。 問題は、ここから始まるんだ」
問題
村木先生の《カード》で描かれる曲線 $C$ はカージオイドらしいと予想しました。
では、曲線 $C$ がカージオイドであることを証明してください。
テトラ「カージオイドであることを証明する……いったい、どうすればいいんでしょうっ!」
僕は考える。
図形の証明はたくさんやったけれど、 「カージオイドであることの証明」なんて習ったことはない。 でも、習ったことがなくても考えることはできる。
僕「この村木先生の《カード》に書かれている曲線 $C$ はカージオイドだと確かめたい。証明したい。 そのためにはどんなことを考えればいいかというと?」
テトラ「どんなことを考えればいいか……これは、あれですよね。 曲線 $C$ がどうなっていれば、カージオイドだといえるかを考えるんじゃありませんか?」
僕「うんうん! そうだよね」
テトラ「あたしの頭には、《定義にかえれ》というポリア先生の言葉がいま浮かびました」
僕「なるほど。すばらしい!」
テトラ「い、いえ、違うんです。 《定義にかえれ》といっても、あたしは、カージオイドの定義を知りません。 たとえば『この曲線 $C$ は円ですか』と聞かれたら、円の定義を思い出します。 そして、曲線 $C$ がその定義に当てはまるかを調べようと思います。でも——カージオイドの定義?」
僕「《定義にかえれ》というテトラちゃんの考え方は、すごく正しいと思うよ。 でも確かに、カージオイドの定義は、円みたいにシンプルに与えられているわけじゃないから、 どう考えていいかわからない」
テトラ「はい」
僕「といっても、僕たちはカージオイドのことを知っている。 僕たちが、どんな曲線のことをカージオイドと呼んでいるかというと、 ひとつの固定された円板があって、同じ半径を持つ別の円板をそのまわりに転がしたときに生まれる曲線だよね(第366回参照)」
テトラ「はい……それはそうです。 そのときに描かれた形をカージオイドと呼んで、 そして、その形と《カード》の曲線 $C$ の形はそっくりだと思います。 向きは $90$ 度傾いてますけれど、形はそっくりです」
僕「うん、だから、《定義にかえれ》で考えるべきことは、 円板のまわりに円板を転がしたときに生まれた曲線と、 この曲線 $C$ とを何とかして結びつけることなんだ」
テトラ「……そこまではわかったように思います。 円板のまわりに円板を転がすというのが、 いわばカージオイドの定義に相当すると考えるわけですね」
僕「そうだね。だって、そうやって描いたものをカージオイドと呼んだから」
テトラ「はい。《あの曲線》——心臓の形をしたあの曲線にカージオイドと名前を付けました。 ですから、《この曲線》——村木先生の《カード》に描く手順が書かれている《この曲線》$C$ と《あの曲線》を結びつけることになります。 はい、そこまでは納得です。 でも、実際のところ、どうやればいいかはさっぱりわかりません!」
僕「まずは名前を付けようか」
テトラ「名前?」
僕「うん。《あの曲線》や《この曲線》だと混乱するから、まずは名前を付けよう。 《円板のまわりに円板を転がして生まれるあの曲線》のことは曲線 $A$ と呼ぶことにしよう。 そして《カード》で示されている曲線はこれまで通り曲線 $C$ と呼ぶ。 曲線 $A$ はカージオイドだとわかっているけれど、 曲線 $C$ はまだカージオイドだと確かめられていない」
テトラ「はい」
僕「だから、僕たちの目標は、 曲線 $A$ と曲線 $C$ は実は同じ曲線だ——と示すことになる」
テトラ「あ、いいですね。名前が付くとはっきりします!」
僕「それで、この二つがどうすれば同じといえるかというと……」

僕とテトラちゃんはしばし、二つの曲線について思いをはせる。
テトラ「……」
僕「いったん、円板のまわりに円板を転がすという発想から離れてみようか」
テトラ「え、せっかく見つけた手がかりを離してしまうんですか」
僕「そういうことじゃなくて、図形的な発想から離れて数式で考えてみるんだ」
テトラ「数式?」
僕「僕たちは、曲線 $A$ のパラメータ表示を知っているよね。 $\theta$ というパラメータを使って、 曲線 $A$ 上にある点 $(x, y)$ のそれぞれの成分を表現できた(第366回参照)」
曲線 $A$ のパラメータ表示(第366回参照)
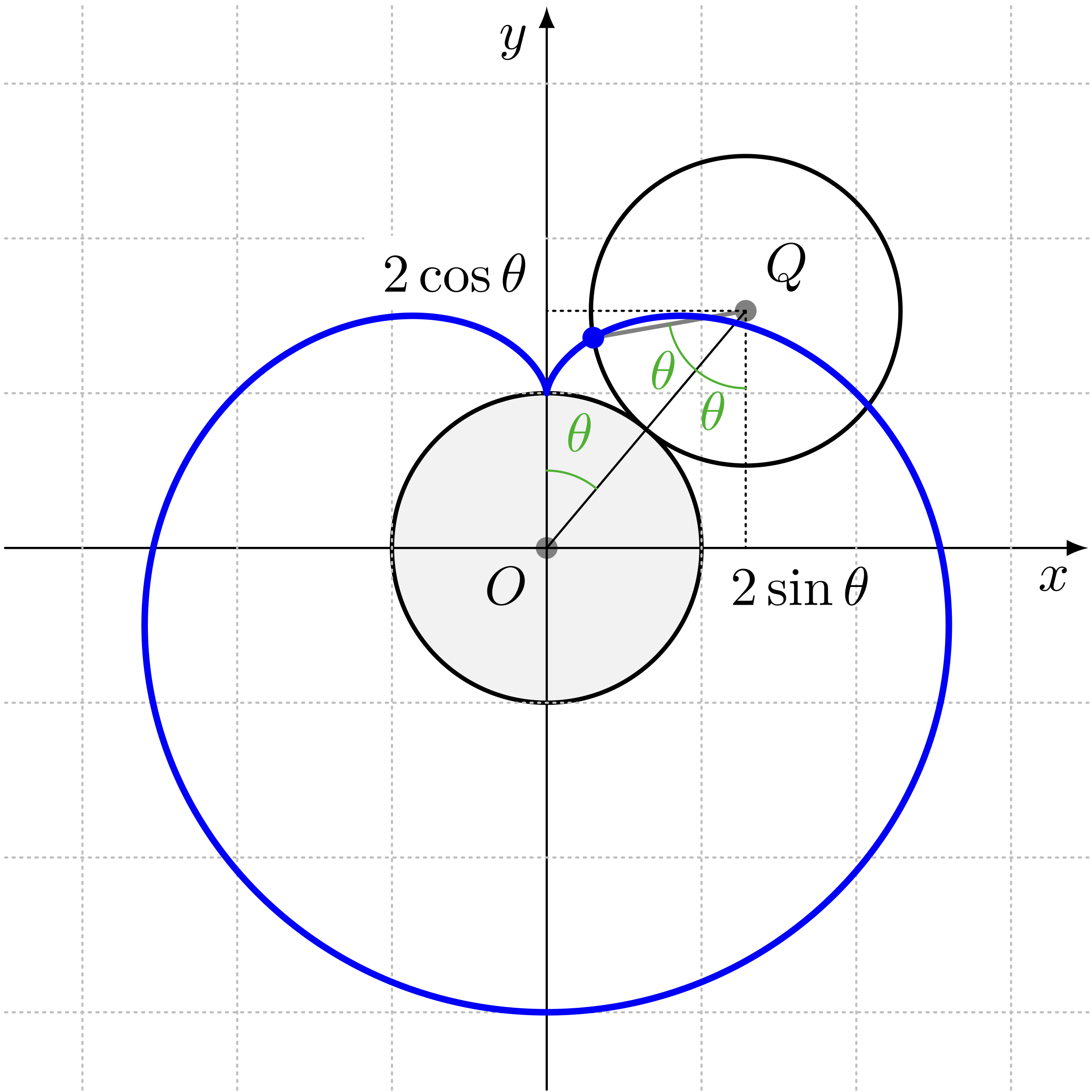
$$ \left\{\begin{array}{llll} x &= 2\sin\theta - \sin2\theta \\ y &= 2\cos\theta - \cos2\theta \end{array}\right. $$
テトラ「そうですね」
僕「だから、 曲線 $A$ を表しているこのパラメータ表示の式を変形してやって、 曲線 $C$ を描ければいいことになるよね。 同じパラメータ表示で描かれる曲線なら、同じ曲線だといえるから」
テトラ「え……」
僕「ただし注意がいる。 曲線 $A$ と曲線 $C$ では向きや位置が違うから、その部分の調整が必要になる。 でもそれは機械的に計算できるはずだから……」
テトラ「……あ、あの! お話の腰を折ってすみませんが、ちょっとお話を聞いていただけますか?」
僕「もちろん。どうぞどうぞ」
テトラ「先輩は、曲線 $A$ をパラメータ表示した式をもとにして、 そこから式変形をして曲線 $C$ を作ろうとなさっているんですよね。 でもそれだと、つまり、何て言うんでしょうか……うまく言えませんけれど、 曲線 $C$ までは結びつかないですよね?」
僕「ええと、ああ、うん、そうだね。テトラちゃんが言いたいのは、 曲線 $A$ から式変形しただけでは曲線 $C$ にはならなくて、 曲線 $C$ を作り出している《カード》の手順と結びつける必要があるんじゃないか、ってこと?」
テトラ「そうです! その通りです。 《カード》の手順にある、《接線》や《垂線》や《交点》のようなものとつなげないことには、 曲線 $A$ と曲線 $C$ が同じ曲線とはいえない——つまり曲線 $C$ がカージオイドとはいえない——と思うんです。 だってその手順に込められた条件が、曲線 $C$ の定義ってことだからです」
僕「テトラちゃんの主張はまったく正しいなあ……。 僕としては、考えを進めるための手がかりとして、すでにわかっている数式を使えないかと思ったんだ。 曲線 $A$ のパラメータ表示はわかってる。 だから、曲線 $C$ に向きと位置を合わせてみたら、何か気付くかもと思ったんだよ」
テトラ「はい」
僕「だけど、 そこまでの話とは別に、《カード》の手順をもとにして曲線 $C$ のパラメータ表示を作らなくちゃいけない。 それはそう。 式が一致すれば、同じ曲線だといえるから、 曲線 $A$ のパラメータ表示と曲線 $C$ のパラメータ表示が一致するかどうかを調べる……という流れになるね」

テトラ「そ、そこなんです。あたしが引っかかるのは」
僕「引っかかるって?」
テトラ「数式——数式はもちろん大切なんですけど、 結局最後に《カード》の手順を考えるのであれば、 最初から曲線 $C$ という図形がどんなものなのかを考えては駄目なのかなと思ったんです。 す、すみません。何だか、先輩のお考えをすべてひっくり返すようなことを言い出して」
僕「いやいや、とんでもないよ。テトラちゃんの方針はまずは曲線 $C$ をよく調べようということだよね」
テトラ「はい、そうです! 曲線 $C$ とまずは《お友達》になりたい……と」
僕「うん、でも、やっぱりどこかでは数式は使うことになると思うけど。二つの曲線が同じ数式で表現できるのを示すのが楽だから。 数式で表現することは《お友達》になったしるしの一つともいえる」

テトラ「数式で表現というのは、曲線のパラメータ表示のことですね?」
僕「いやいや、それに限らないよ。曲線の表現方法はいろいろある」
テトラ「?」
僕「つまりね、曲線を表現するためには、パラメータ表示や、方程式や、極方程式などがある。だから、そのどれかに帰着させればいい」
テトラ「ああ、なるほどです」
僕「たとえば、原点中心で半径 $1$ の円といえば、 《平面上にあって、原点からの距離が $1$ である点全体の集合》だけど、 いろんな表現方法があるよね」
原点中心で半径 $1$ の円の《パラメータ表示》
$$ \left\{\begin{array}{llll} x &= \cos\theta \\ y &= \sin\theta \end{array}\right. $$
原点中心で半径 $1$ の円の《方程式》
$$ x^2 + y^2 = 1 $$
原点中心で半径 $1$ の円の《極方程式》
$$ r = 1 $$
テトラ「はいはい、わかります、わかります。表現方法は違うけれど、同じ曲線を表しています」
僕「それで、と。 テトラちゃんは曲線 $C$ はどんなものかを考えるところからスタートしたいんだね。 うん、じゃあ、その方針で行くことにしよう」
テトラ「はい!」
僕「曲線 $C$ を作り出しているのは動く点 $P$ だけど、それを図に描くとこうなる」

テトラ「そうですね。点 $R$ は円 $Q$ 上の点で、そのときの接線は $\ell$ で、直線 $m$ は原点を通り直線 $\ell$ に垂直な直線です。 ここからわかることは——」
僕「うん。あ、そうか。点 $R$ は接点だから——」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2022年9月9日)