第367回 シーズン37 エピソード7

曲線を追いかける（前編）

《カード》がやってきた

僕「テトラちゃん、勉強中？」

テトラ「あっ、先輩！　村木先生からの《カード》です。 おもしろそうな《お楽しみ》をいただいたんですよ」

僕「《カード》は久しぶりだね。どんな問題だろう」

テトラ「はい。問題というか何というか……」

僕「うん？」

テトラ「先日、サイクロイドやカージオイドを描いたじゃないですか」

僕「うん、楽しかったね」

テトラ「あの話をレポートにまとめて、村木先生に持っていったんですよ」

僕「なるほど。研究発表だ」

テトラ「そ、そんなすごい内容じゃないんですが……ともかく、 直線上を円板が転がるときのサイクロイド（第365回参照）、 固定した円板の回りを別の円板が転がるときのカージオイド（第366回参照）について先生に話したんです。 そうしたら……」

僕「そうしたら《カード》がプレゼントされた、と」

テトラ「ですです。 円板が転がってできる曲線っておもしろいですねって言ったら、 こんな曲線はどうかなって……」

僕「おっと、ずいぶん複雑な手順だね。接線に垂線を引く？」

テトラ「そうなんですよ。 今回の《カード》は、特に何かを求める問題じゃないし、証明する問題でもありません。 ただ、点 $P$ が描く曲線 $C$ について考察せよというものでした。 考察……つまり、その曲線 $C$ がどんなものかを検討して、確かめてみなさいってことですよね」

僕「そうだね。 それで、テトラちゃんはどういうことを考察しようと思ったの？」

テトラ「は、はい。 いま考え始めたばかりですけれど、 まずはとにかく《図を描こう》と思っています。 正確にどんな図形になるか、どんな曲線が生まれるかはわかりませんけれど、 だいたいの図を描くところから始めようかな、と思いました」

僕「うん、それは大事だよね」

テトラ「先輩は先日、《極端な値》で試したり《考えやすい値》で試したりしましたよね（第366回参照）。 あのときと同じように、主な点を選べば、 曲線のだいたいの形がわかるかなと思ったんです」

僕「なるほど」

テトラ「主な点を何点か描いたら、それを滑らかに結べば、曲線の形がわかりますよね……あはははっ！」

僕「ど、どうしたの？」

テトラ「すみませんっ！　ちょ、ちょっと思い出し笑いをしてしまいました。 先日、別の問題を考えているときに『滑らかに……結ぶ』と言いながら曲線を描いたんですが、 かなりデコボコしちゃって、口では『滑らか』と言ってるのに、図はぜんぜん滑らかじゃなかった、 というのを思い出していました」

僕「点を滑らかに結んで曲線を描くのって難しいよね」

条件の再確認

テトラ「し、失礼しました。笑いがなかなか止まらなくて……まずは、 《カード》の手順を再確認していきますっ！」

僕「ええと、僕は話を聞いていてもいいの？」

テトラ「もちろんです。あ、もしもお邪魔でなければ、ですけれど」

僕「いや、僕の方が邪魔してなければいいんだ」

テトラ「曲線 $C$ について考察をするんですけれど、 その曲線 $C$ は点 $P$ が描くことで作られます。 ですから、点 $P$ がどんなふうに決まるかを理解する必要があります」

僕「……」

テトラ「で、ですよね？」

僕「大丈夫。僕は、なるほどなあ……と思いながら聞いているんだから、どうぞどうぞ先に進めてください」

テトラ「点 $P$ がどんなふうに決まるか。それは《カード》に手順が書いてあります。 最初に舞台設定として円 $Q$ が固定されています。中心が点 $Q(2,0)$ で半径が $2$ の円です」

僕「うん。円は中心と半径が決まれば決まるから、円 $Q$ はもう決定。そしてこの円 $Q$ は動かない」

テトラ「そうですね。 それから次に、点 $R$ を接点とする接線 $\ell$ を引く……とありました。 点 $R$ は、どこでもいいんですが、円 $Q$ の円周上にある点でなければいけません。 そしてもちろん、接点 $R$ を決めれば接線 $\ell$ も決まります」

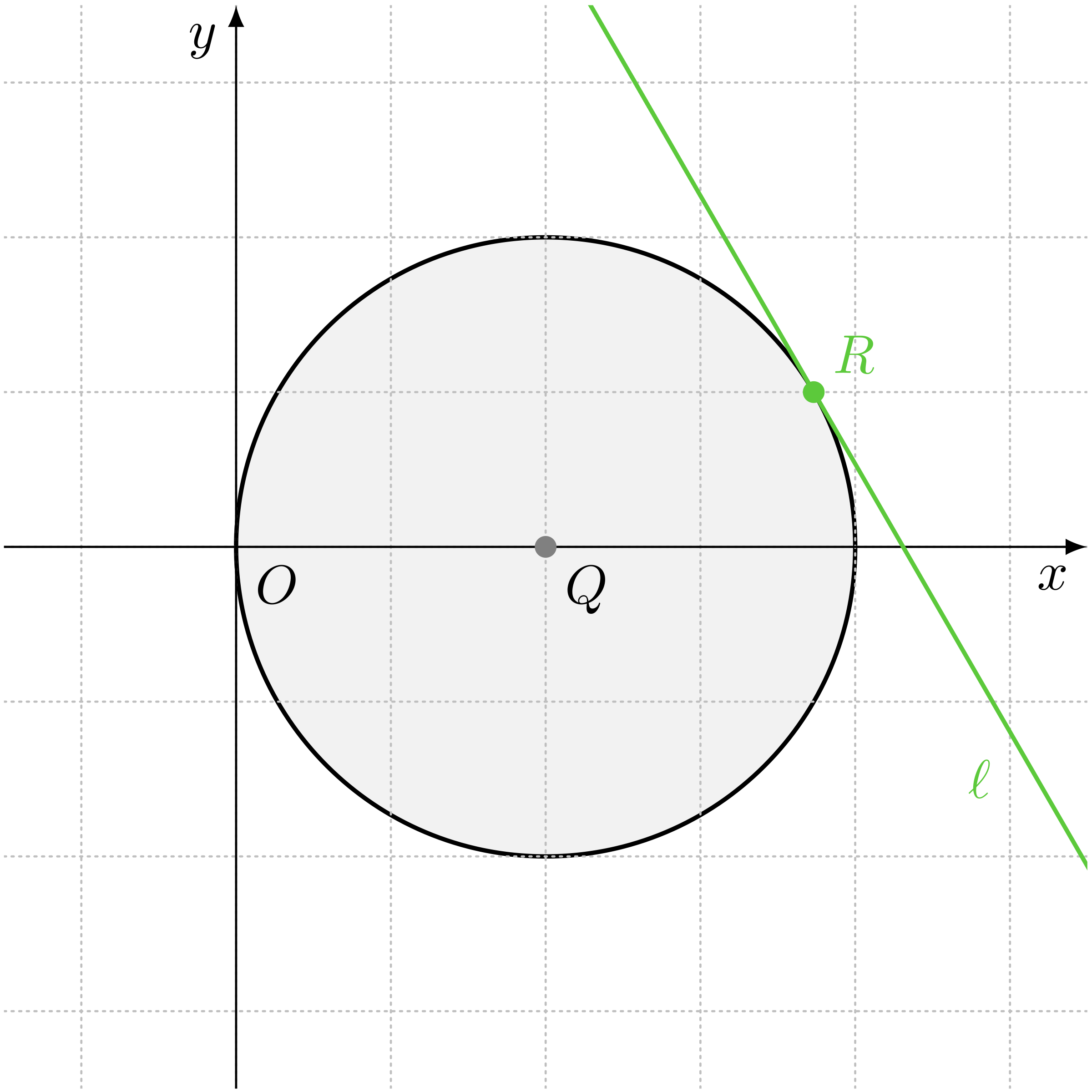
テトラ「点 $R$ は円 $Q$ 上の一点ということだけが決まっています。 ですから、もしも点 $R$ が円周の別のところにあったら、 接線 $\ell$ もそれに応じて別のところに引くことになります。 でも、どこにあったとしても直線 $\ell$ はいつも円 $Q$ に対する接線ですし、 点 $R$ はいつも接点になっています。 そういう性質は守らなくてはいけません……と、この《カード》は主張しています」

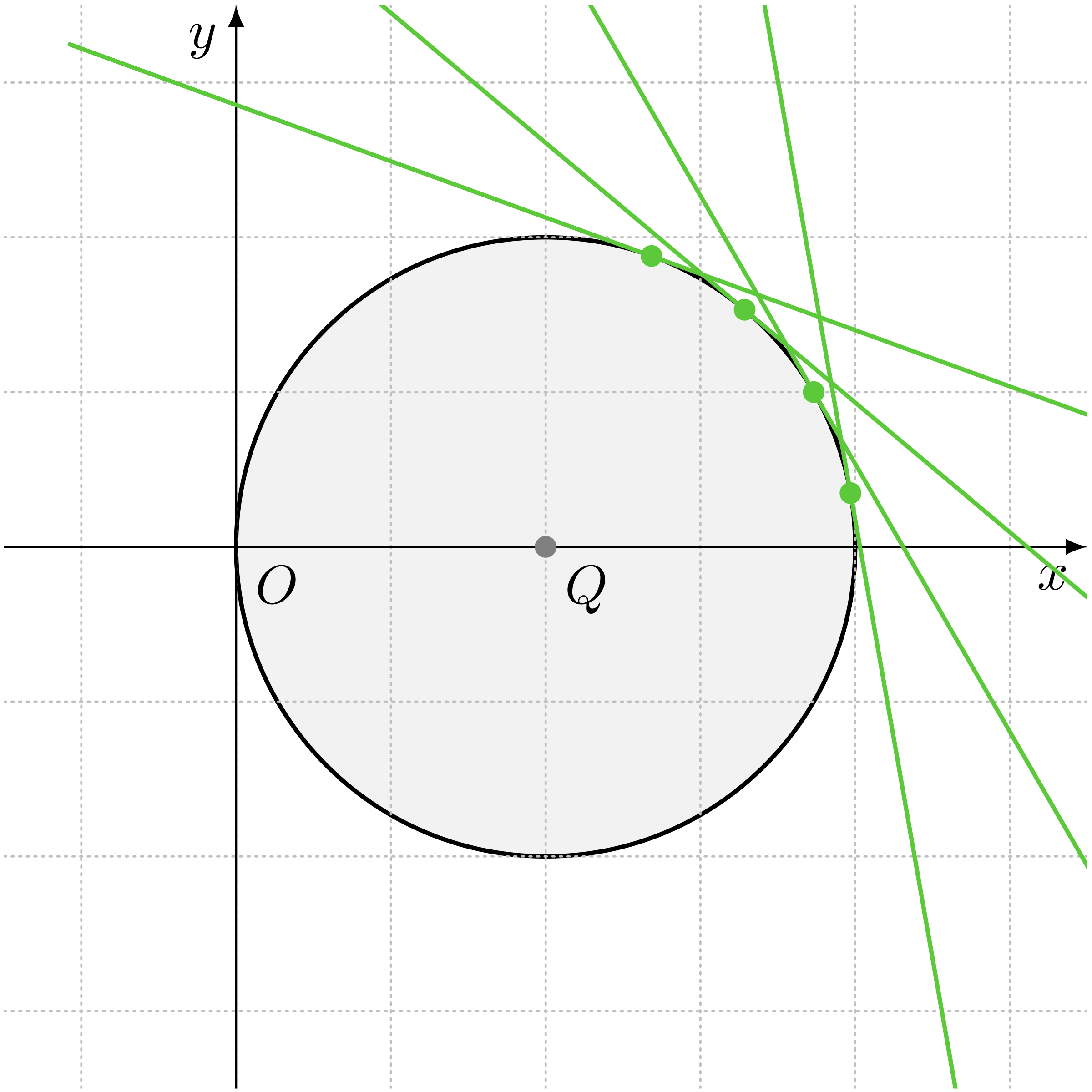
僕「うん、いいよ。テトラちゃん、ていねいに進んでいるなあ」

テトラ「あ、はい。先日のサイクロイドでも、カージオイドでも、 最初は難しそうに見えたんですが、結局、あたしにもよく理解できました。 難しそうに見える図形でも、一歩一歩きちんと追うのが大事なんだ……と思ったんです」

僕「うんうん、大事だよね」

テトラ「ですから最近は、一歩一歩きちんと追うのがマイブームなんですっ！」

僕「マイブーム」

テトラ「引き続き、《カード》を読んでいきます。一歩、一歩、…… 原点 $O(0,0)$ から接線 $\ell$ に対して垂線 $m$ を引きます。 そして、二直線 $\ell$ と $m$ の交点を $P$ とします。 $m$ は $\ell$ に対する垂線ですから、 $\ell$ と $m$ は直交することになります。直角です！」

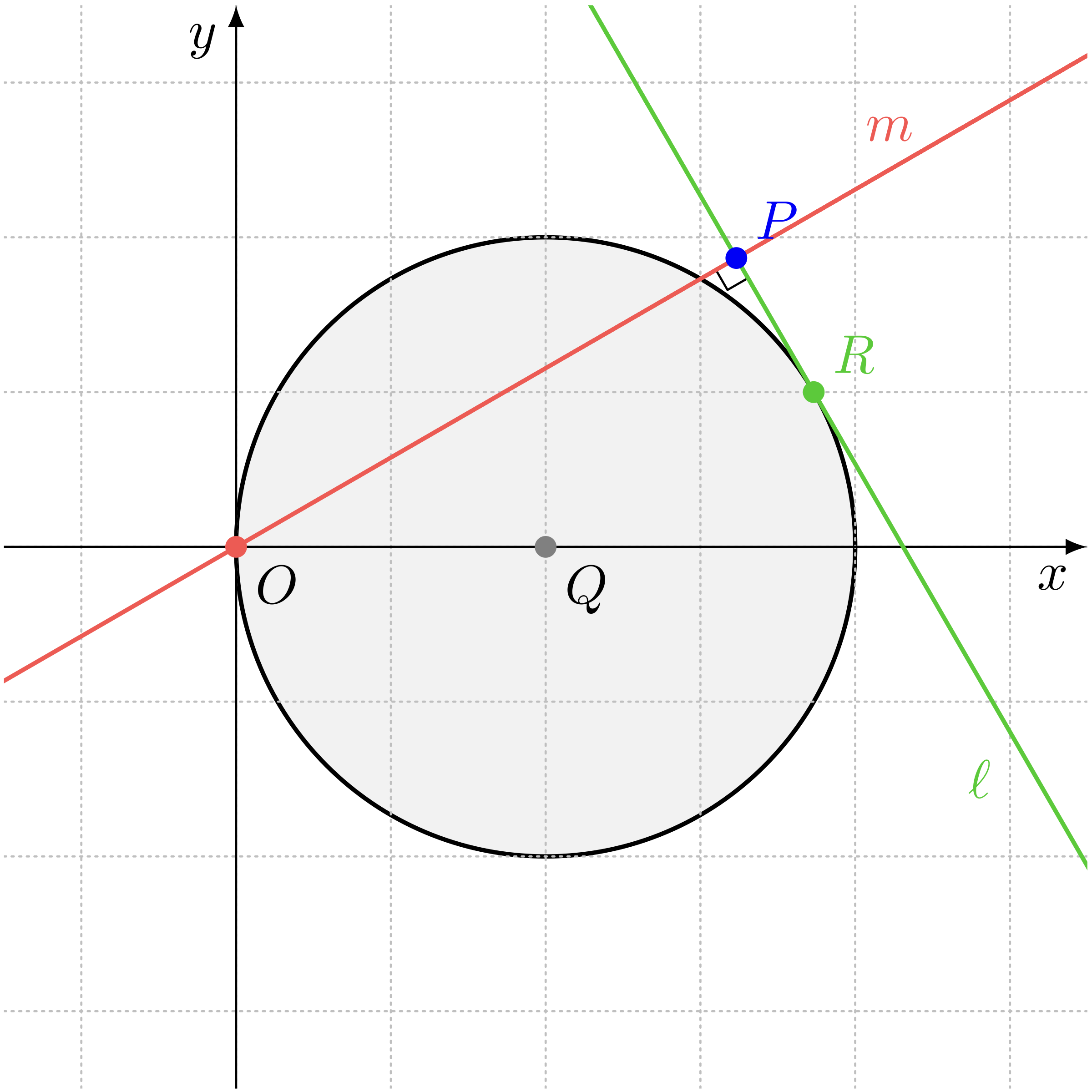
僕「うん。点 $P$ は、原点から直線 $\ell$ に下ろした垂線の足ということだ」

テトラ「あ、はい、そうですね。《垂線の足》っておもしろい表現ですよね」

僕「そうだね。それで、と。これで点 $P$ まで来たね。 点 $R$ を決めると直線 $\ell$ が決まって、 そこから直線 $m$ が決まって、点 $P$ が決まる」

テトラ「はいっ。ここから、点 $R$ が円 $Q$ を一周するようすを考えます。 そうすると、点 $R$ が動くことで、直線 $\ell$ も動きます。 そして直線 $\ell$ が動くことで、直線 $m$ も動き……そして、 $\ell$ と $m$ の交点 $P$ も動きます」

僕「その点 $P$ が描く曲線 $C$ を考える」

テトラ「さっきも考えましたけれど、点 $P$ の動きを想像すると、 たぶんですけど、点 $P$ は円 $Q$ の外側にかぶさるように……こんな動きをするんじゃないでしょうか。 つまり、これが曲線 $C$ ？」