![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。 好奇心旺盛で根気強い《元気少女》。言葉が大好き。
ミルカさん:数学が好きな高校生。 僕のクラスメート。長い黒髪の《饒舌才媛》。
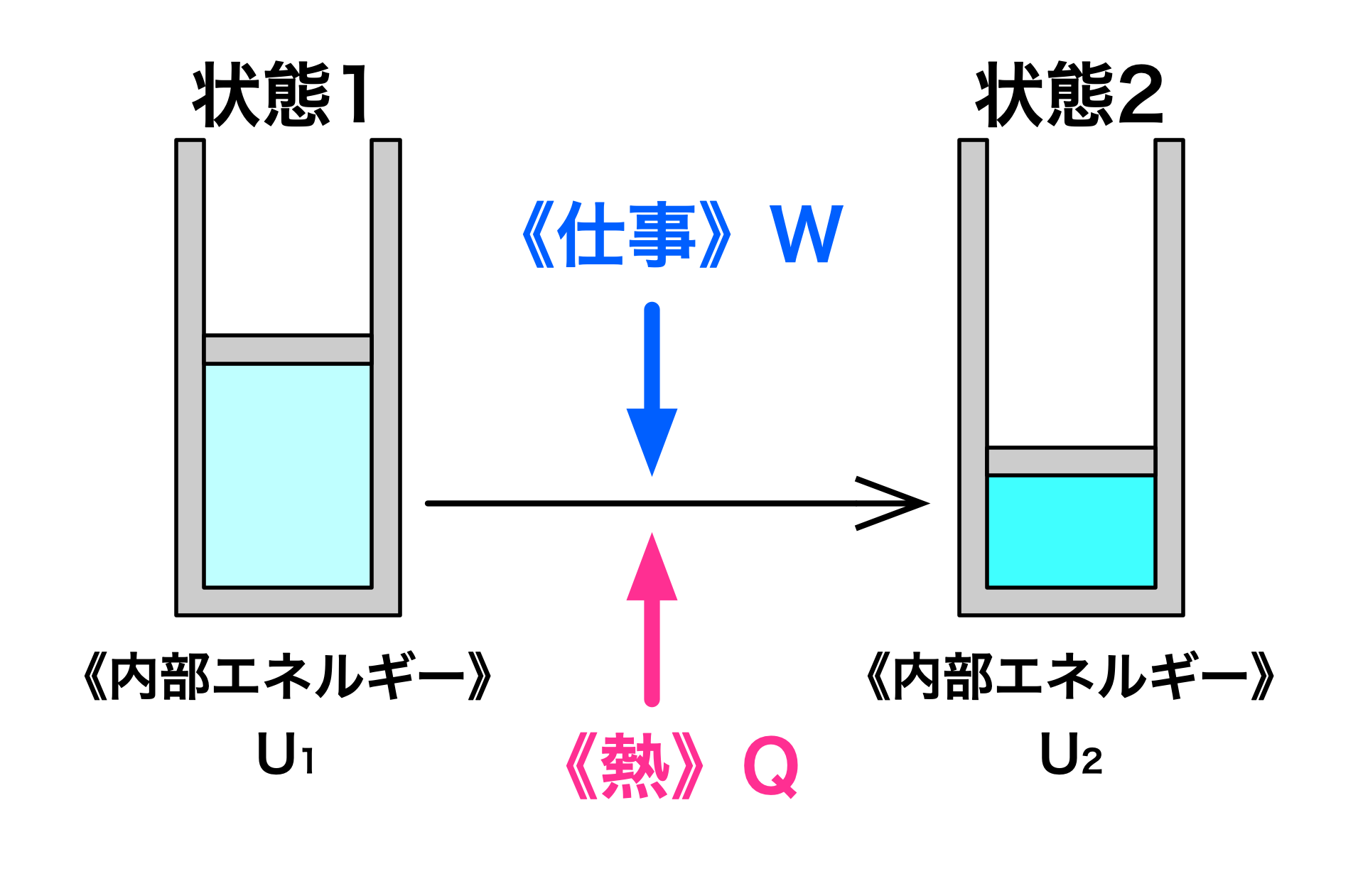
熱力学第一法則(再掲)
このとき、 $$ U_2 - U_1 = Q + W $$ が成り立つ。 $U_2 - U_1$ を $\Delta U$ と表すと、 $$ \Delta U = Q + W $$ が成り立つ。
これを熱力学第一法則という。
ミルカ「《圧力》《体積》《物質量》《温度》など、状態が持っている物理量のことを一般に状態量(じょうたいりょう)という」
テトラ「状態量」
ミルカ「理想気体の状態方程式は、理想気体において、状態量が互いにどのような関係を持っているかを表現した式といえる。 状態1の理想気体に対して、《熱》や《仕事》を与える操作を行って状態2になったとする。 状態1と状態2ではそれぞれに状態量は違うかもしれない。しかしどちらでも理想気体の状態方程式は成り立っている。 しかし、どちらの式にも《熱》や《仕事》は出てこない。《熱》や《仕事》は状態量ではないからだ」
$$ p_1V_1 = n_1RT_1 \qquad\longrightarrow\qquad p_2V_2 = n_2RT_2 $$テトラ「なるほどっ! テトラ、納得ですっ! テトラは『状態について理解した状態』になりましたっ!」
ミルカ「それでは、状態についてさらに理解を高める問いを出そう」
テトラ「え?」
ミルカ「『この気体は《温度》が $T$ の状態にある』というとき、私たちはある前提を置いている。それはどんな前提だろうか」
僕「……」
テトラ「『この気体は《温度》が $T$ の状態にある』という表現は、何かまずいんでしょうか。 《温度》は状態が持っている物理量……状態量ですよね?」
ミルカ「表現がまずいわけではない。ただ、忘れがちな前提があるというだけのこと」
テトラ「何でしょう……温度計が存在するとか?」
ミルカ「それは確かにそうだが、いまはその話ではない。そもそも《温度》が $T$ と定まるかという話」
テトラ「《温度》が定まらない場合というのがあるんでしょうか?」
僕「ああ、そういうこと?」
テトラ「たとえば、《温度》が絶え間なく上がったり下がったりするような状況をおっしゃっています?」
ミルカ「違う。そのような場合も上がったり下がったりする《温度》というものはあるだろう? そうではなく、 そもそも《温度》が定まらない場合がある。 私たちが物理学で『《温度》を $T$ とする』というためには、《温度》が定まらなくてはならない」
テトラ「テトラは白旗を上げた状態に変化しました……ミルカさんのおっしゃる《温度》が定まらない状況が想像できません。 先輩は、わかってるんですよね?」
僕「うん、ミルカさんが言ってるのは平衡状態(へいこうじょうたい)のことだと思うよ。 平衡状態になければ《温度》は決まらない」
ミルカ「そうだ。平衡状態のことを言ってる。熱力学に限定して考えるなら熱平衡(ねつへいこう)と呼ぶこともある」
テトラ「平衡状態とは、どういうものでしょう」
ミルカ「マクロな視点から見ると変化していない状態を平衡状態という」
テトラ「変化していない? ぐ、具体的に……」
ミルカ「低温の気体Aと高温の気体Bが入った容器があって、あいだに仕切りが入っているとする。 マクロな視点から見るとどちらの気体も変化していないから、平衡状態にある。 そして、気体Aと気体Bの《温度》は定まっている」
テトラ「はい……」

ミルカ「この仕切りを取ると、気体Aと気体Bは混じり始める。 そうするとマクロな視点から見るとこの容器の内部は変化していることになる。これは平衡状態ではない状態、つまり非平衡状態だ。 このとき、容器内にある気体の《温度》は定まらない」
テトラ「なるほど。温かい気体と冷たい気体がぐしゃぐしゃと混じり合っている途中……だからですね」
テトラちゃんは『ぐしゃぐしゃ』と言いながら両手をこね合わせた。
ミルカ「やがてしばらくすると、気体Aと気体Bはすっかり混じり合い、マクロな視点から見るとの容器の内部は変化していない状態になる。 これが平衡状態。そしてこのとき容器内にある気体の《温度》が定まる」
僕「こういうケースもあるよ。 たとえばシリンダーのピストンを乱暴にがちゃがちゃ動かしている途中は、 シリンダーの中の気体はぐるんぐるん渦を巻いたり、まるで嵐のような状態になる。 シリンダー内部の気体が均一じゃなくなる。それが非平衡状態。 でも、ピストンを動かすのをやめて少し待てば、シリンダーの中の気体は均一になる。 それが平衡状態だよ」
テトラ「ははあ……」
僕「シリンダーの中の気体が均一な状態でなかったら、 気体の《温度》や気体の《圧力》ということはできないよね。 だって、シリンダーの中のこの場所とあの場所が違う状態になっていて、 しかも時間ごとにぐるんぐるん変化するとしたら『気体の《温度》は $T$ です』なんていえない」

テトラ「《温度》が定まらないという表現の意味がわかってきました。 テトラは平衡状態を理解したと思います! もう変化しない状態が平衡状態ですね……あらら、でも、そんなこと、ありえるんでしょうか」
僕「ありえないと思うの?」
テトラ「気体分子運動論で計算をしましたが、気体の《温度》は結局、ええと、ええと、気体分子の運動エネルギーの平均じゃないですか(第347回参照)。 ということは気体分子が速度を持っているから《温度》があるわけですよね。 気体分子が飛びまわっているのに、気体が変化せずにスーンとしているというのは、ちょっと……」
ミルカ「気体が、マクロな視点から見ると変化しないというところが重要」
テトラ「マクロな視点から見ると変化しない……なるほど! あたしがいま言った『気体分子が飛びまわっている』というのはミクロな視点ですね。 気体分子はぶんぶん飛びまわっているけれど、気体全体として見るときには変化していないように見える状態……そういうことなんですね」
僕「容器の各部分に注目したときに、こっちの気体分子の運動エネルギーの平均と、あっちの気体分子の運動エネルギーの平均とが等しいと考えてもいいよね。 気体分子は飛びまわっているけれど、あっちとこっちでその飛びまわり方に違いがない」
テトラ「理解しました!」
ミルカ「熱力学で、特に断りなく状態といったときには、平衡状態を指すことが多い。 平衡状態ではない状態……非平衡状態……を考えているときには、それをはっきり述べる必要がある」
テトラ「はい……そこまではわかりました。それから、状態という言葉、ものすごく自然に使っているこの言葉が、深い意味を持っていることもわかりました」
そこで、ミルカさんが急に無言になる。
ミルカ「……」
テトラ「……?」
ミルカ「平衡状態の話を聞いたテトラは、今回は《いつもの疑問》を出してこないのかな?」
テトラ「あ、あたしの疑問? いつもの疑問って何でしたっけ?」
ミルカ「『こ、これって新たな物理法則が導入されたんでしょうか?』」
僕「うわ!」
ミルカさんがテトラちゃんのモノマネをすると、なかなかの破壊力があるな……破壊力ってなんだ。
テトラ「平衡状態が物理法則と関係するんですか?」
ミルカ「熱力学的な系を長時間放置すると平衡状態に達する。すなわち、マクロな視点から見ると変化しない状態に達する。 このことは私たちが知っている経験的な事実だ。 だから、熱力学ではこの事実を物理法則として導入し、議論を進める。 この法則を熱力学第ゼロ法則と呼ぶ場合もある」
僕「へえ」
テトラ「熱力学第ゼロ法則!」
ミルカ「ただ、何を熱力学第ゼロ法則と呼ぶかは、場合によって違う。 熱平衡に関する推移律のことを熱力学第ゼロ法則と呼ぶ場合もある」
僕「推移律! 物理学に推移律が出てくるの?」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2022年1月28日)