![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
僕「……だから、アボガドロの法則は、同じ圧力・同じ体積・同じ温度の気体中には同じ数の気体分子があるという法則といえる」
《圧力》《体積》《温度》が同じ箱には、気体の種類によらず同じ数の分子がはいっている
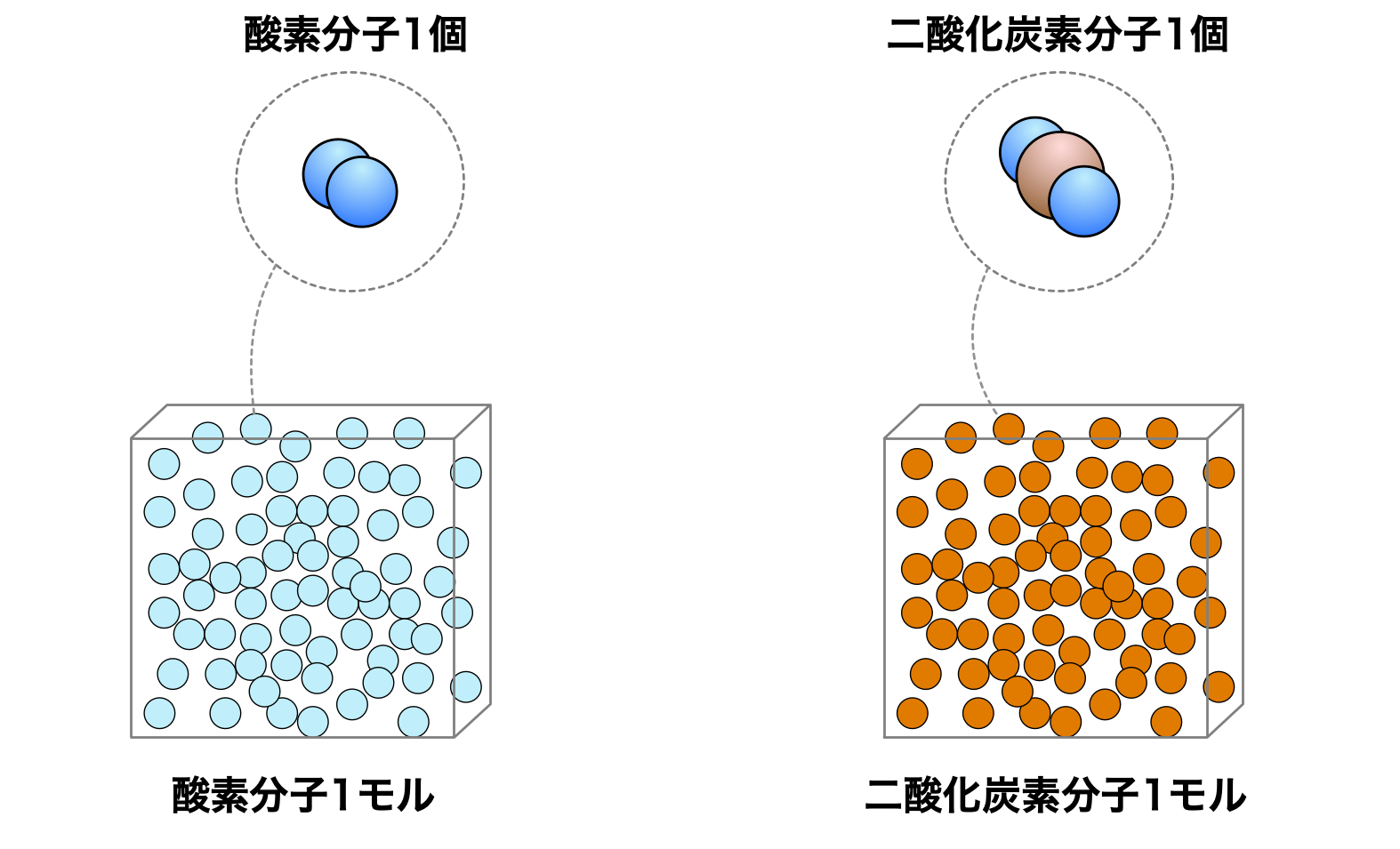
ユーリ「酸素でも、二酸化炭素でも、空気でも」
僕「そうだね。空気は何種類かの物質の混合気体になるけれど、それでも同じ。気体の種類はなんでも、《圧力》と《体積》と《温度》を決めれば気体分子の個数も決まる」
ユーリ「《物質量》」
僕「うん、気体分子の個数が決まるというのは《物質量》が決まるといってもいい」
ユーリ「それがモル」
僕「そうだね。モルは《物質量》の単位だから、《圧力》と《体積》と《温度》が決まれば、その気体分子が何モルあるかがわかることになる」
ユーリ「1モルの気体に $6 \times 10^{23}$ 個の分子があるのはわかったけど、 実際のとこ、どのくらいの量なのかよくわかんない」
僕「ええとね、確か22.4L(リットル)だよ」
ユーリ「むむ? それは《体積》でしょ?」
僕「ごめんごめん。関連する物理量をぜんぶ言わなきゃだめだよね。 《圧力》が1気圧で、 《体積》が22.4L(リットル)で、 《温度》が0℃の気体があったとすると、その気体の《物質量》は1モルになる」
ユーリ「ふーん……」
僕「言い方を変えると、 《物質量》が1モルの気体の《圧力》を1気圧にして、 《温度》を0℃にしたら、 《体積》は22.4Lに決まる」
ユーリ「22.4リットルってどのくらいなの?」
僕「冷蔵庫に1リットルの牛乳パックがあるよね」
ユーリ「てことは、牛乳パック22.4本分? あっ、けっこう大きいね!」
僕「熱気球のとき、 《圧力》《体積》《温度》などをいっぺんに考えるとややこしいという話をしてた(第342回参照)」
ユーリ「あんときは《物質量》もいっぺんに考えてたのかー! 熱気球に開口部があるってことは、 風船の中の《物質量》も変化しちゃうから」
僕「確かにそう。空気が出入りするからね。 アボガドロの法則は、 複数の物理量に関係があることをものすごく単純に表現しているすごい法則だけど、 《圧力》《体積》《温度》《物質量》……といういろんな物理量を一度に考えるとややこしい。 だから、変化する物理量を少なくしてやれば考えやすくなる。 たとえば《温度》を一定にして……」
ユーリ「ちょっと待って、お兄ちゃん」
僕「ん?」
ユーリ「アボガドロの法則にでてくる物理量って、 ゆーて《圧力》《体積》《温度》《物質量》じゃん? 四つ。 でも、物理量ってめちゃめちゃたくさんあるよね?」
僕「うん、そうだね。物理量同士を組み合わせて計算したものも物理量だし、 新しく定義することもできるから、 実質的には無数にある」
ユーリ「その無数の中から《圧力》《体積》《温度》《物質量》の四つを選ぶって、 ものすごいことじゃない? もしかして」
僕「いやまったくユーリのいうとおりだと思うよ。ものすごいこと。 とてつもなくすごいこと。しかも単純な法則だし」
ユーリ「だよねー……ふむう」
僕「……」
ユーリ「あのね。ニュートンの運動方程式もそうだよね。《力》《質量》《加速度》の三つ」
僕「うん」
ユーリ「万有引力の法則もそう。《力》《質量》《距離》の三つ。 ぜんぶ、すごく物理量の個数が少ないじゃん?」
僕「そうだね。オームの法則は《電流》《電圧》《抵抗》の三つだし、 クーロンの法則は《力》《電気量》《距離》の三つ」
ユーリ「……ぜんぶ、めちゃめちゃすごい!と思う!!」
僕「うん」
ユーリ「反応うすいぞー!」
僕「いや、なるほどなあって思ってたんだよ」
ユーリ「たとえばさー、『物理法則を発見しました! 123個の物理量の関係です! ◯◯の法則と呼びます!』と言われても困るじゃん」
僕「わかるよ。そんなにたくさんの物理量に関係を見つけたとしたら、それはそれですごいけど」
ユーリ「それもそーか」
僕「四個の物理量だけでも、同時に全部変化したら、定量的に調べるのは難しくなる。 たとえば理科で習うボイルの法則は、《圧力》《体積》《温度》《物質量》のうち、 《温度》と《物質量》を一定にして考えているのがわかる……というか、《圧力》と《体積》だけが変化するようにしたときに、互いの関係を発見したんだろうけれど……」
ボイルの法則
このとき、《圧力》と《体積》の積は一定である。Aを定数とすると、
$$ pV = A\quad\textrm{(一定)} $$
と表せる。
ユーリ「ボイルの法則って、反比例じゃなかったっけ。《圧力》を二倍にすると《体積》は半分になる」
僕「同じことをいってるよね」
ユーリ「そっか。《圧力》2倍で《体積》1/2だと、掛ければ変わんないか……」
僕「ボイルの法則の説明では、気体が入っているこういうシリンダーの図がよく出てくる。気体を押すことができるピストンが入っている」
ピストンが付いているシリンダー
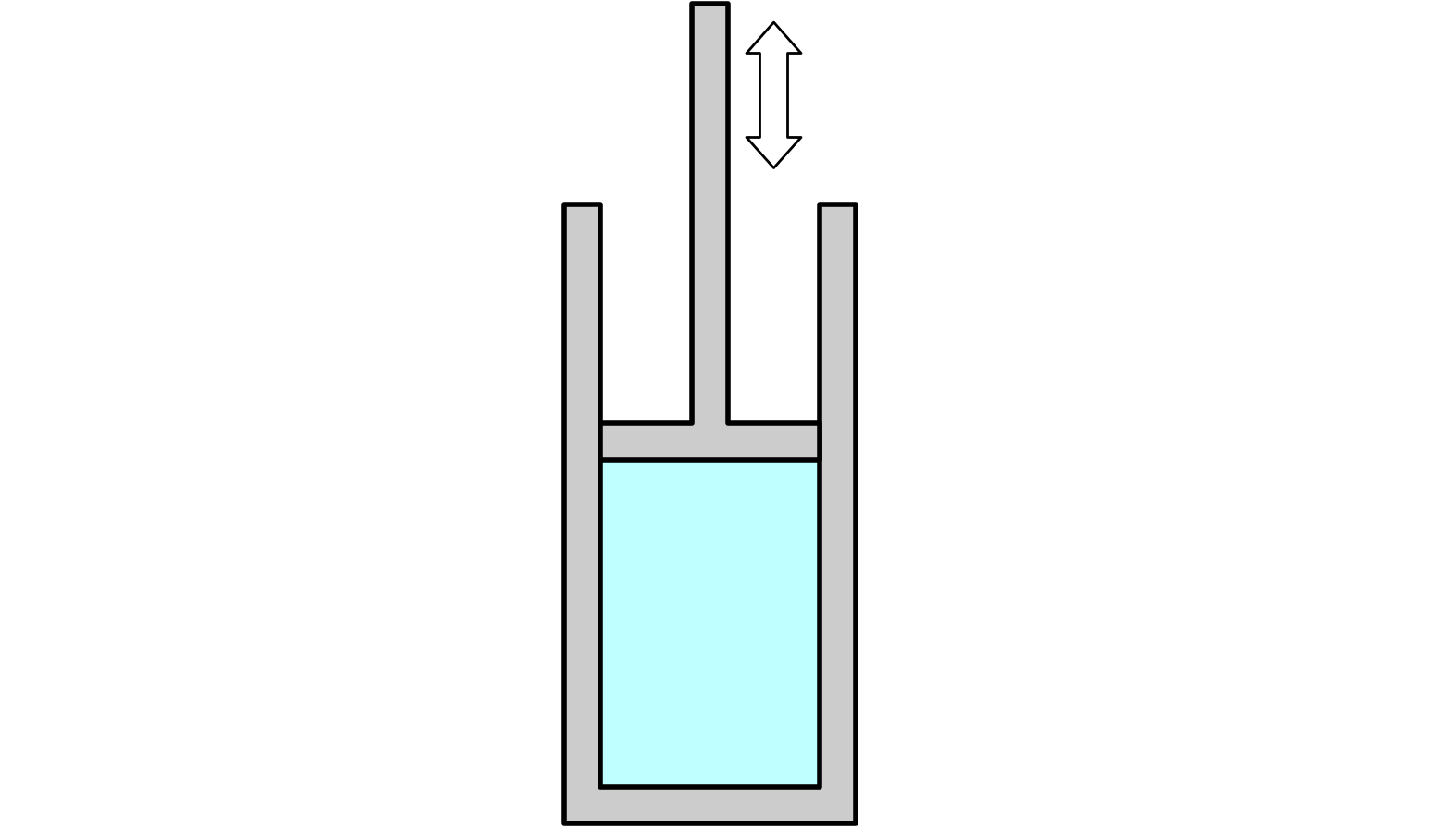
ユーリ「ぎゅっと押すんでしょ」
僕「そうだね。ピストンを押すとシリンダー内部の《圧力》は増加して、気体の《体積》は減少する。 ボイルの法則から、 《物質量》が一定で、《温度》が一定という条件のもとで、《圧力》が2倍になったとき、《体積》は1/2倍になっている。 こんなふうにピストンに重りを乗せる場合もある。質量が2倍の重りを乗せればピストンに掛かる重力が2倍になるから、《圧力》も2倍になる」
ピストンに重りを乗せる

ユーリ「……」
僕「質量が2倍の重りを乗せると、ピストンに掛かる重力の大きさは2倍になる。 《圧力》は単位面積あたりに掛かる力のこと。つまり、力を面積で割ればいい。ピストンの面積は変わらないから、重力の大きさが2倍になれば、《圧力》も2倍になる。 《圧力》の定義は大丈夫?」
ユーリ「《圧力》の定義はいいけど、わかんなくなった! 《体積》って、気体の体積だよね? 《圧力》って気体の圧力じゃないの? ピストンの圧力なの?」
僕「ああ、そうだね。ごめん。いろいろ説明を省略してしまったねえ。 ちゃんと順を追って考えていこう」
ユーリ「そーそー」
僕「まず、ピストンに重りを乗せるとピストンは下がっていく。 そしてしばらくすると、ピストンは動かなくなる。 そのときに重りに掛かる力を図示するとこうなる。重りに注目してるわけだ」
重りに掛かる力

ユーリ「これはわかる。《地球が重りを引く力》が重力で、《ピストンが重りを押す力》はその力の反作用でしょ?」
僕「いや、《地球が重りを引く力》が重力なのはいいけど、《ピストンが重りを押す力》はその力の反作用じゃないよ。 《地球が重りを引く力》を作用の力とすると、《重りが地球を引く力》が反作用の力。 地球から重りに力が掛かると、重りから地球に向きが反対で大きさが等しい力がかかる。これが作用・反作用の法則」
ユーリ「あっ、そーなんだ」
僕「AからBに働く力を作用の力とすると、BからAに働く力が反作用の力なんだ。AとBが入れ替わるところが大事」
【宣伝タイム】
テトラ「作用・反作用の法則については、こちらの一冊『ベクトルの真実』をごらんくださいっ! Web立ち読みのところにも含まれています(p.9)」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2021年12月24日)