第342回 シーズン35 エピソード2

熱気球はなぜ浮かぶ？（後編）アボガドロの法則

僕の部屋

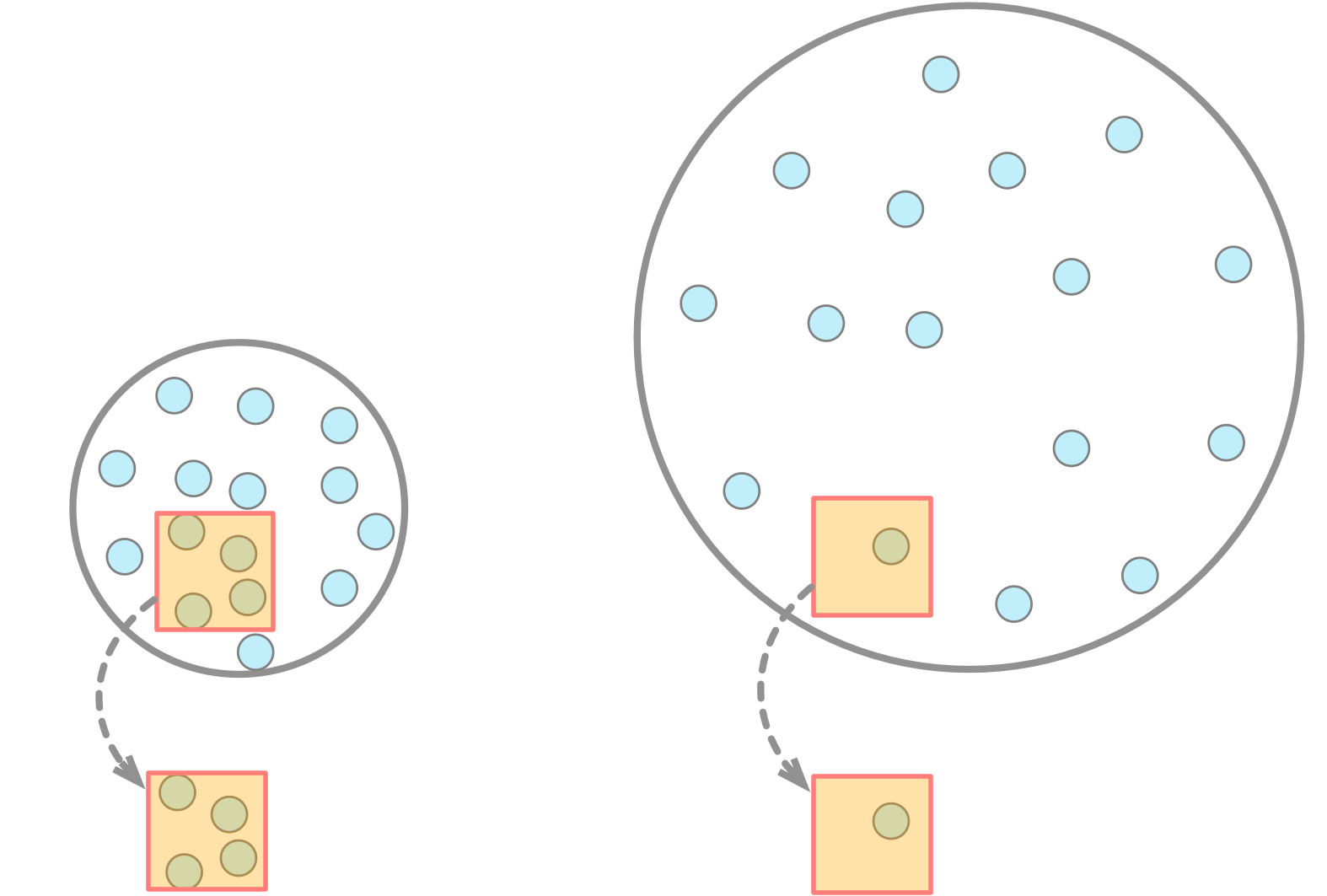
僕「熱気球に話を戻そう。熱気球の中の空気を温めると、熱気球の中にある空気は密度が小さくなる。 つまり、単位体積当たりの分子の個数が少なくなる。だから軽くなる」

• 《熱気球で押しのけた空気の重さ》が浮力の大きさで、鉛直方向上向き。
• 《熱気球の中にある空気の重さ》と《熱気球自体（風船とゴンドラとバーナー）の重さ》を足したのが重力の大きさで、鉛直方向下向き。

ユーリ「この差で浮かぶんだね。カンペキに理解した！……あれ、ちょっと待って」

僕「ん？」

ユーリ「熱気球だったらいーけど……いや、熱気球でもダメじゃね？」

僕「何がダメなんだろう。熱気球が浮かぶかどうかという話？」

ユーリ「んーとね、熱気球が浮かぶのは浮力があるからだよね」

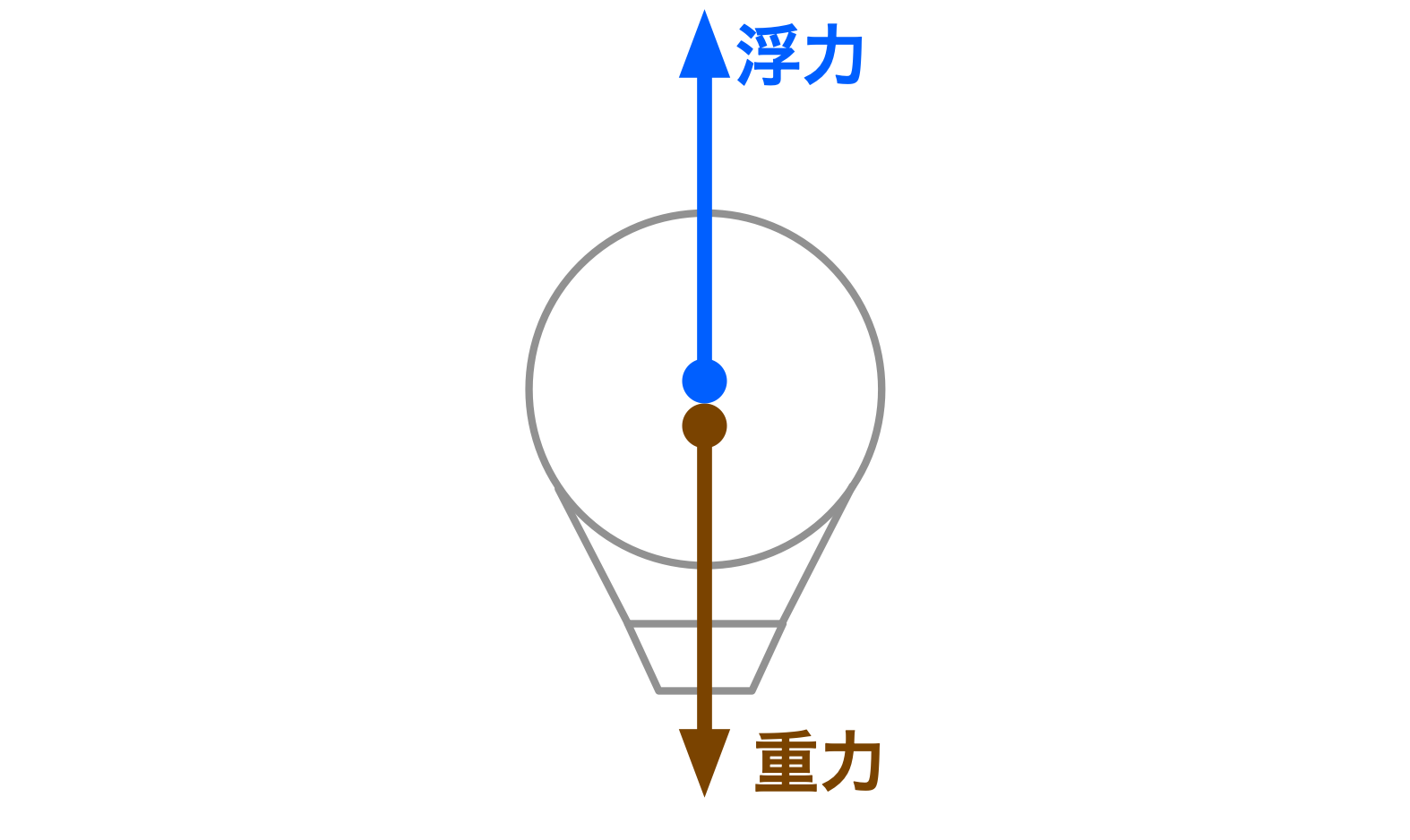
僕「そうだね。浮力と重力を合わせた合力が鉛直上向きになるから」

ユーリ「でも、熱気球の中の空気にも重さがあるから、よく考えないといけなくて……」

僕「その通りだね。何がダメなんだろう」

ユーリ「話しながら考えてるんだから、ちょっと待ってよー」

僕「はいはい」

ユーリ「風船とゴンドラとバーナーの重さは考えないとして……《熱気球で押しのけた空気の重さ》と《熱気球の中にある空気の重さ》の差が大事で……」

僕「……」

ユーリ「さっきお兄ちゃんは密度が大事だっていったよね。密度が小さいから軽くなるって」

僕「うん、そうだよ」

ユーリ「でも、さっきの図みたいに風船がぶわっと膨らんだら密度は小さくなるけど、熱気球ってそんなに膨らむ？」

僕「ああ、なるほど。ユーリはそういうところを気にしていたんだね。 現実世界の熱気球を考えるときには、けっこう細かいところまで気にしないといけないから難しいよ。 熱気球を組み立てて、空気を中にいれてやると、しぼんでいた風船部分がだんだん大きくなる。 十分に膨らんでから、さらにバーナーで中の空気を温めると、 風船部分はもうそんなに大きくならなくても、中の空気の温度は高くなっていく」

ユーリ「そこそこ！　風船部分は大きくならないけど、中の空気の温度が高くなるんでしょ？　だったら、 密度は小さくならないじゃん！　体積が大きくならなきゃダメだもん！　 だったら、温めても軽くならないじゃん！　何か変だぞー」

僕「ユーリの推理は正しいんだけど、それはあくまで風船部分が閉じた空間の場合なんだよ」

ユーリ「閉じた空間？」

僕「うん。 熱気球の風船部分にたまっている空気が、外に漏れたりしないし、 もちろん中にも空気が入ってこないとするということ。 そのとき初めて、体積が大きくならなければ密度は小さくならないといえる」

ユーリ「あ」

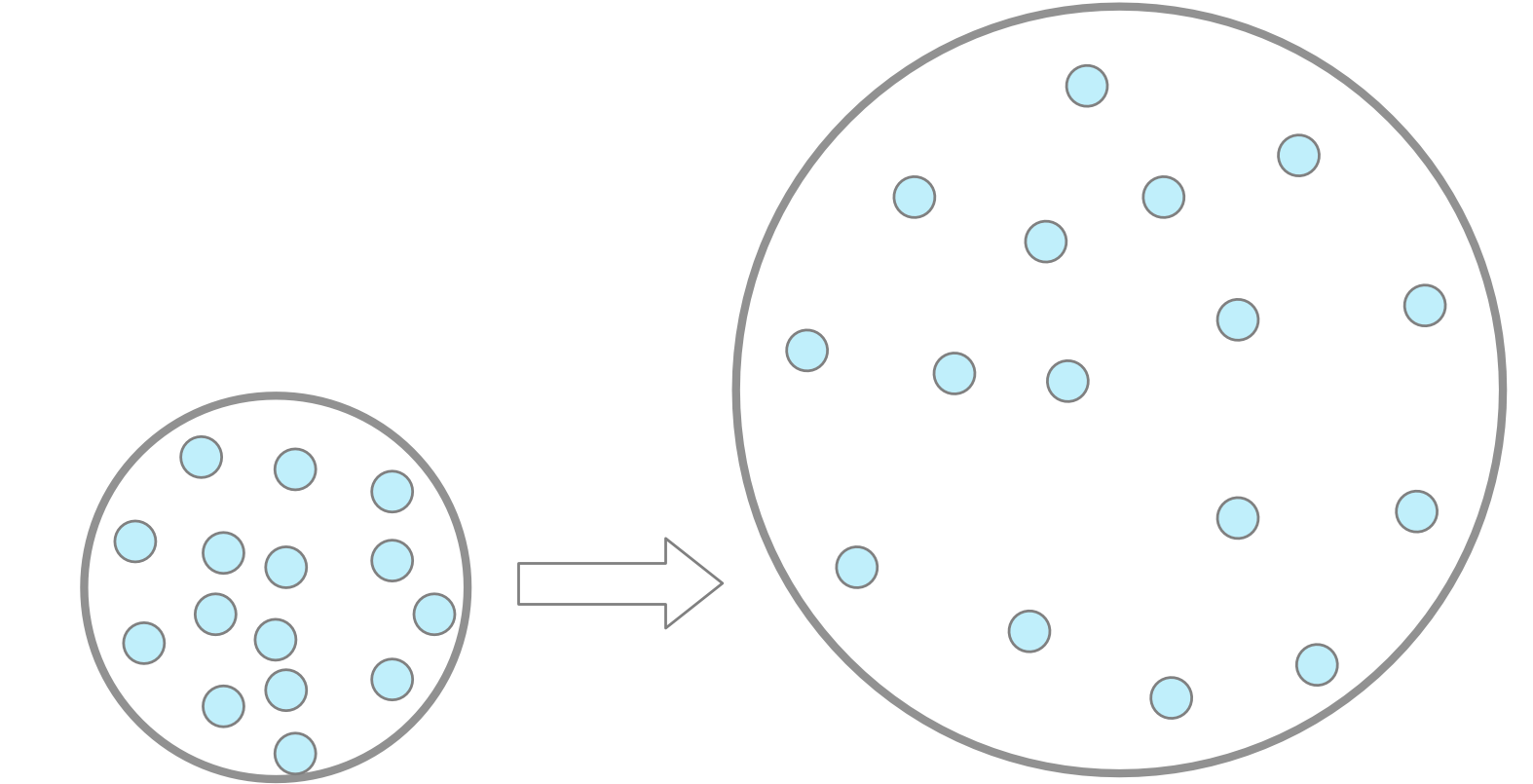
僕「閉じた風船が大きく膨らむと体積は大きくなる。 そのとき風船の中に入っている空気の密度は下がる。それはそう」

ユーリ「うん」

僕「でも風船の大きさが変わらずに……つまり体積が一定のままで……空気が漏れていったとしても密度は下がる」

ユーリ「あー、わかった！」

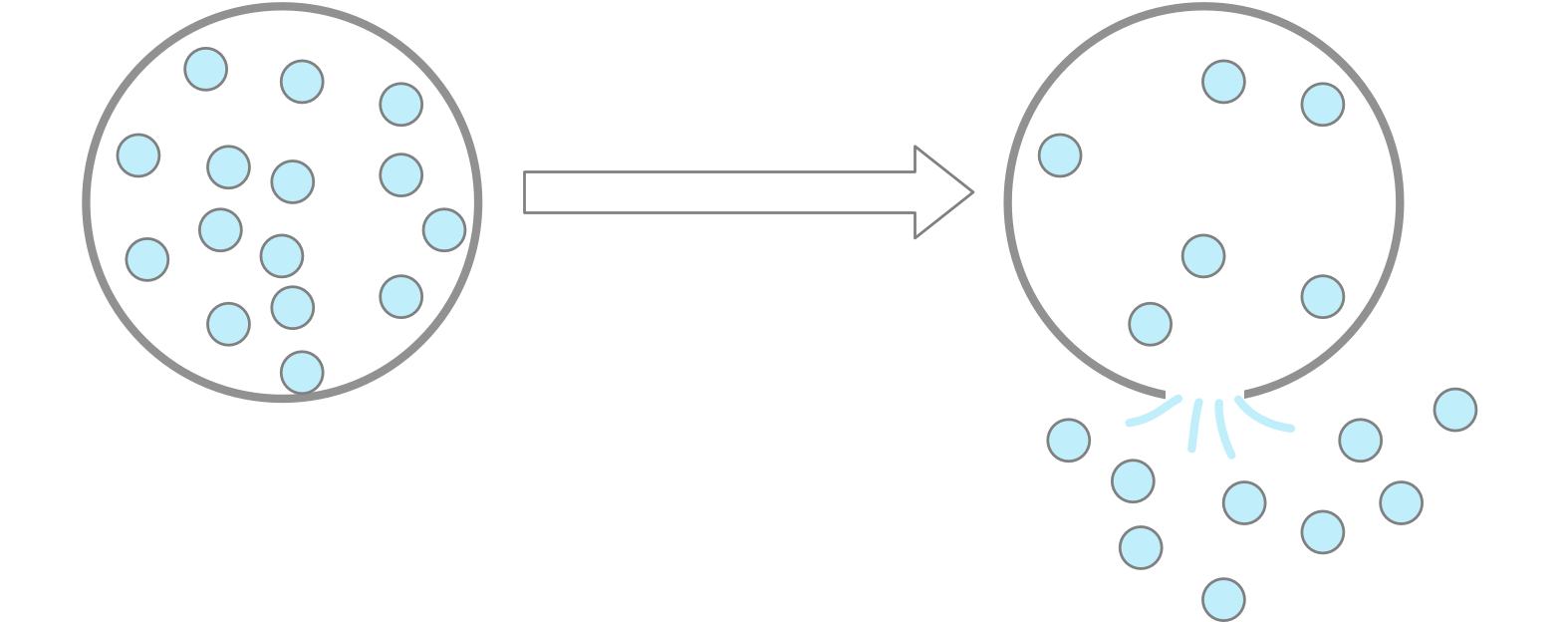
僕「わかった？」

ユーリ「ん？　ありゃ？　またわかんなくなった。 風船部分から空気を漏らしたら、体積減るじゃん！　ぷしゅーって風船はつぶれるよね。 体積一定のままで空気を漏らすなんてできるの？」

僕「ユーリ、ユーリ。よく想像してみて。 バーナーで空気を温めて、空気の温度を上げる。そうすると、風船中の空気の分子が激しく動いて体積を増やそうとする。 でも、もう熱気球は膨らまないとする」

ユーリ「風船がパンパンに膨らんでるとき？」

僕「そうだね。空気の温度を上げて、空気の分子が風船を膨らまそうとするけれど、 もう膨らまない。風船の体積はもう増えない。 そうすると熱気球の開いている口……開口部から、空気の分子が漏れ出ていくんだ」

ユーリ「そっか。風船をつぶして空気をぷしゅーと抜くんじゃなくて、あふれ出る感じ？」

僕「そうそう、そういう感じ」

ユーリ「風船部分がパンパンに膨らんで圧力が高くなって、空気が出てくんだね！」

僕「だいたいはそういう感じ」

ユーリ「だいたいなんだ」

僕「うん。現実世界の熱気球のようすを正確に表すのはなかなか難しいから」

ユーリ「何が難しいの？」

僕「バーナーの炎の勢いがどうなるか。バーナーに近い場所と遠い場所の温度差。外からの風から受ける力。 外部の温度差。風船も完全な球体じゃない。だから、厳密な数式を立てるのは難しいだろうね」

ユーリ「来た来た。何でも数式で解決しようとする数式マニアめ！　何でも数式で解決できると思うんじゃにゃい！」

僕「いや、だから数式を立てるのは難しいって言ってるんだけど」

ユーリ「そっか……数式じゃなくても、『空気を温めると熱気球は浮かぶ』だけでもややこしー！」

物理量

僕「いろんなことを一度に考えようとすると、どうしてもややこしくなる。 さっきから、ユーリはいろんなことを一度に考えようとしていたよね」

ユーリ「そーだっけ？」

僕「そうだよ。とても大事な物理量がぽんぽん出てきてた」

• 《圧力》が高くなって……
• 《体積》が大きくなって……
• 《温度》が高くなって……

ユーリ「物理量……」

僕「うん、物理学ではいろんな物理量を使って、物体の運動や状態を表していく。 物理量を測定したり、物理量が何を表しているかをよく考えたりする。 物理学的な法則は、物理量の関係として表される」

ユーリ「急に難しい話になってきた」

僕「そんなことないよ。たとえばユーリは、テレビが言ってた『熱の力』って表現に引っかかっていたよね（第341回参照）。 これは、物体の運動で出てくる《力》とは違うぞって気付いた。 それは《力》という物理量を知ってるから」

ユーリ「ニュートンが出てきた。運動方程式……だっけ？」

僕「そうだね。質点に《力》を書けると、《加速度》が生じる。 《力》と《質量》がわかると、生じる《加速度》がわかる。 その関係を表したのがニュートンの運動方程式で、 それは《力》と《質量》と《加速度》という三つの物理量の関係を、$$F = ma$$という一つの式で表しているといえるわけだ」

【ＣＭ】

テトラ「ニュートンの運動方程式、万有引力の法則、力学的エネルギー保存則……力学の基本はこちらからどうぞ！」

僕「ＣＭがはさまった」

ユーリ「そっか。《力》《質量》《加速度》も物理量なんだ」

僕「そうだね。物体の運動を考えるときには《力》《質量》《加速度》などは重要な物理量になる」

ユーリ「《圧力》《体積》《温度》も物理量？」

僕「そうだよ。熱気球を考えているときに出てきた《圧力》《体積》《温度》などは重要な物理量だ」

ユーリ「もしかして、物理量ってたくさんある？」