第339回 シーズン34 エピソード9

式と概念、意味と比喩（前編）

図書室にて

僕「……テトラちゃんって、引っかかったところを抜けると、急激に理解が進むんだね」

テトラ「え、あ、はい……それにしても、数式で表されたときに、 その各部分が読み解けると、とっても楽しいですねえっ！」

• 重力加速度 $g$ は単位質量に掛かる力なので、 $mg$ は質量 $m$ の質点に掛かる力になる。
• 電場 $E$ は単位電荷に掛かる力なので、 $qE$ は電気量 $q$ の電荷に掛かる力になる。

僕「そうだね」

テトラ「すごく納得です！　 ひとつひとつの文字が何を意味しているかだけじゃなくて、 割り算や掛け算で新しいものがポコポコ生まれてくるみたいです」

僕「ポコポコ」

テトラ「だってそうですよね。 $g, mg, mgh$ と並べると、重力場でのそれぞれの意味がわかります。 同じように $E, qE, qEh$ と並べると、電場でのそれぞれの意味がわかります」

僕「……」

テトラ「力と変位の積を仕事と定義するなら、 どんな世界にいったとしても、 『この世界での力はどうなっているのかな？』と考えて『位置の変化はどうなっているかな？』と考えればいいんです。 重力でも静電気力でも、そこの部分は変わりませんよね。 その世界での力がわかって、その世界での位置の変化がわかれば、 積で仕事がわかります。それがおもしろいですっ！」

僕「……」

テトラ「先輩？」

僕「……うん、テトラちゃんの整理の仕方を味わっていたんだよ。 $g, mg, mgh$ と並べる。 $E, qE, qEh$ と並べる。そこから、さらに考えを進めてみることもできるよね。 たとえばテトラちゃんは、$$gh$$という式をみたらどんなふうに考える？」

テトラ「なるほどです。 $g, mg, mgh$ という式に対応して概念を考えることができるので、 $gh$ という式はどんな概念かということですね……」

僕「そうそう」

テトラ「重力加速度と高さの積ということですから……あっ、いえっ、違います。そうなんだけど、そうじゃないですね。他の式との関係で考えた方がよさそうです」

僕「うんうん」

テトラ「$gh$ というものを、 $mgh/m$ として考えます。 そして、ええと、 $mgh$ は《重力による位置エネルギー》ですから、 $mgh/m = gh$ というのは《単位質量あたりの、重力による位置エネルギー》といえますっ！」

• $mgh$ は《重力による位置エネルギー》
• $gh$ は《単位質量あたりの、重力による位置エネルギー》

僕「すごいなあ！　テトラちゃんは応用力があるよね」

テトラ「き、恐縮です。先ほど、《重力加速度》を《単位質量あたりに掛かる重力》と見なしたときと同じ発想を使ってみましたっ！　《◯◯で割る》というのは、 《単位◯◯あたりの量》を作る計算ですから（第338回参照）」

僕「こういうことだね」

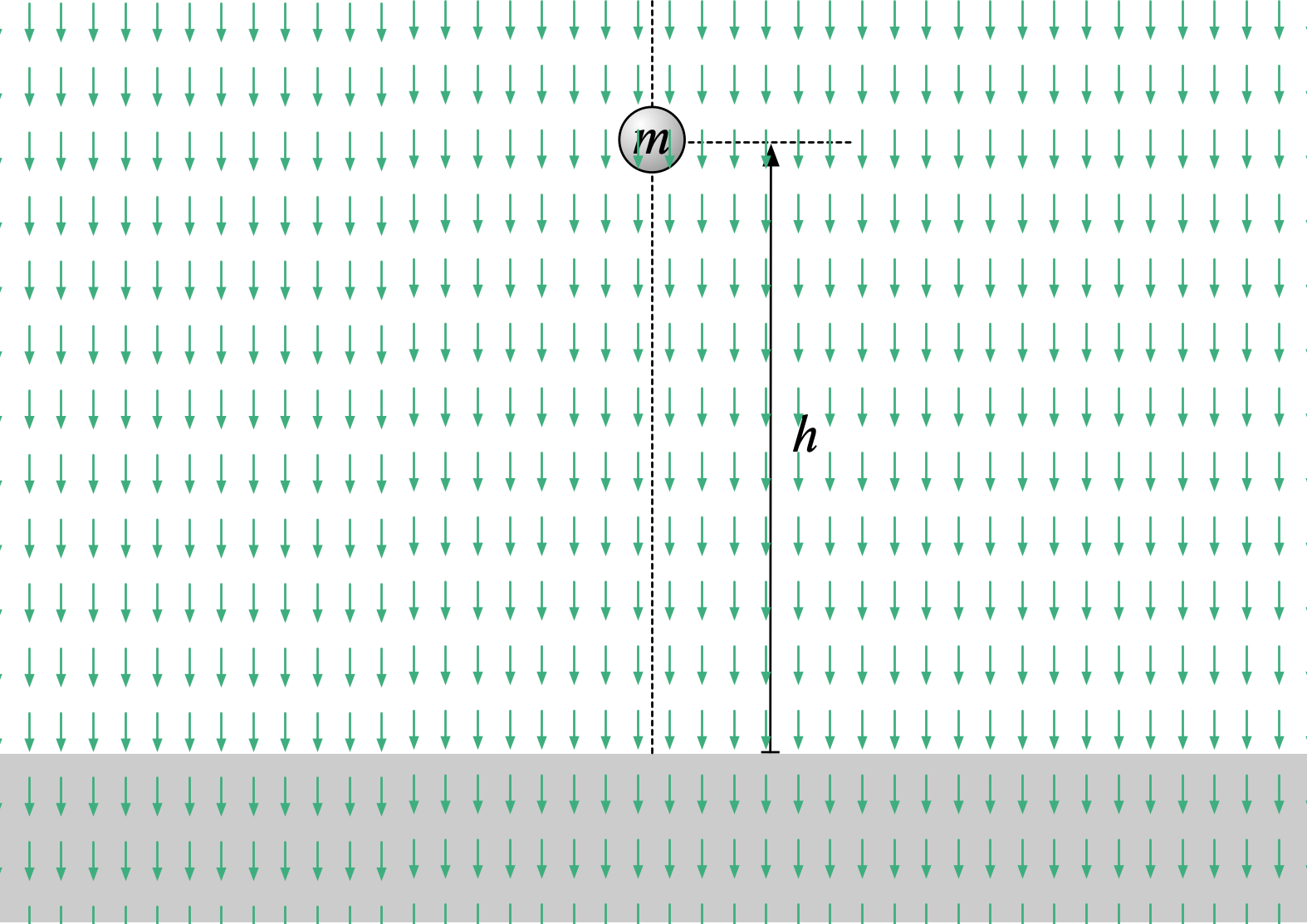
テトラ「そうです、そうです。 $gh$ は《単位質量あたりの、重力による位置エネルギー》ですから、これに質量を掛ければ位置エネルギーが得られます。 あっ！　先輩、話の道筋が見えちゃいましたよ」

僕「え？」

テトラ「あたしたちはいま、式の形がそっくりな《重力場の世界》と《静電気力の世界》を行き来していますよね。 ということは、いま《重力場》について考えたのと同じことを《静電気力》で考えることができるんですね？」

僕「テトラちゃん、鋭いね！」

テトラ「それは《式の形》を考えればすぐに得られます。 つまり $E, qE, qEh$ から類推して$$Eh$$の意味を考えるわけですから。 $Eh$ は《単位電荷あたりの、静電気力による位置エネルギー》といえますね。 テトラ、これには自信がありますっ！」

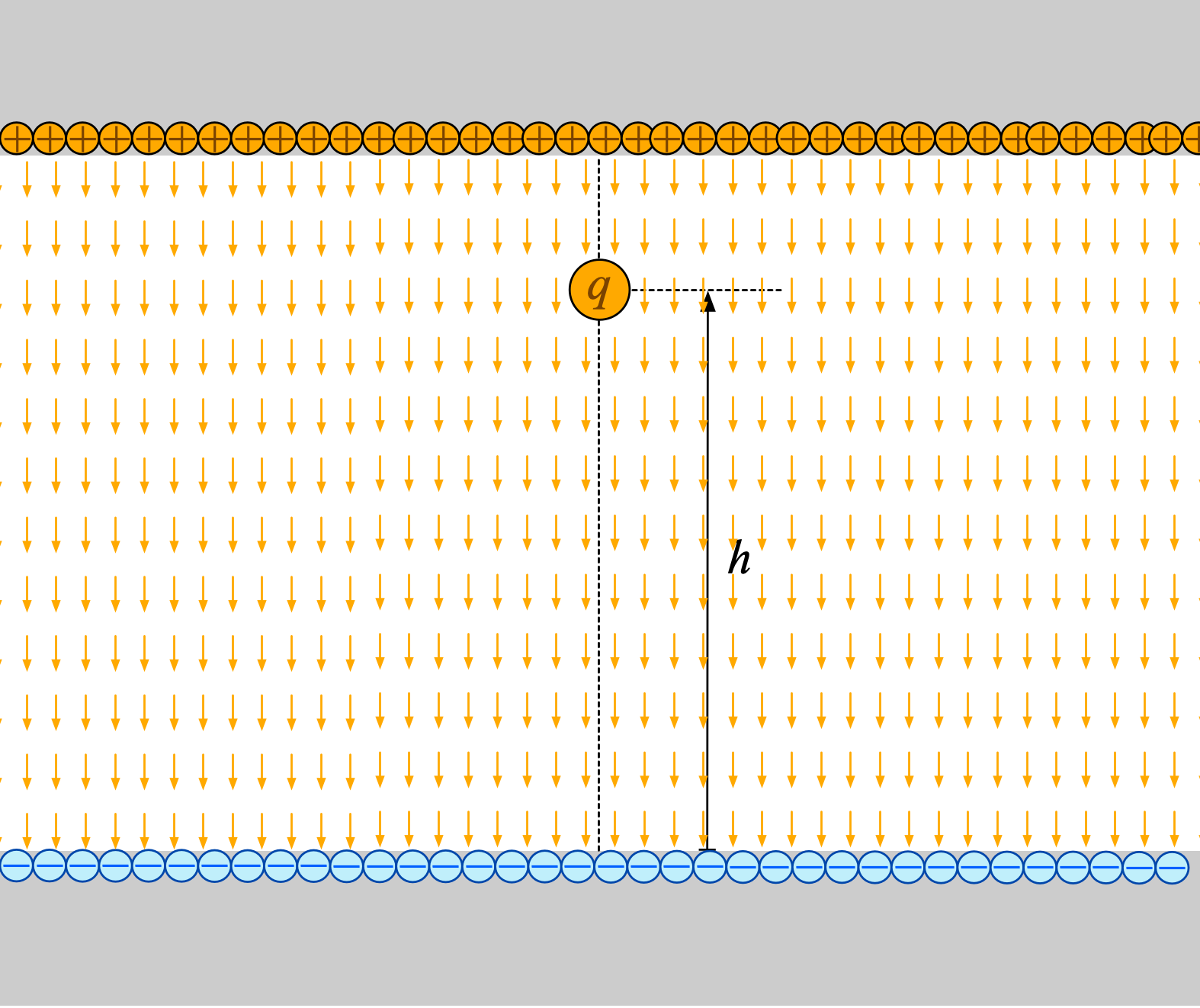
僕「そうだね！」

テトラ「式の各部分の意味はこんなふうにまとめられそうです！」

僕「ああ、これはいいねえ……すごく納得がいく！」

比喩としての「高さ」

テトラ「《重力場》と《静電場》は、とてもきれいに対応がつきます。 《力》と《高さ》をしっかりつかまえれば、抽象的な概念でも《式の形》を武器にして進めますっ！」

僕「そうだね。テトラちゃんの理解はとても正しいんだけど……テトラちゃんが言った《高さ》について、念のため確認。 電場でいう《高さ》は、あくまで電場による位置エネルギーの基準点から、電場による力の向きを考えたときの位置のことだというのはいいよね？」

テトラ「……といいますと？」

僕「いや、ほら、僕たちが日常的にいう《高さ》というのは、重力をイメージしているから、 重力と静電気力を混同していないよね、というだけの確認。 コンデンサ自体がどちらの向きになっていても、静電気力の $h$ はあくまで電場の向きで考えている」

テトラ「あ、はい。それは大丈夫です。気付いていませんでしたけれど、 『静電気力に抗する力を掛けて $h$ だけ移動するときの仕事』を考えていましたから、 そこは誤解していないと思います」

僕「物理の教科書では、静電気力による位置エネルギーを $qEd$ のように表現してたよ」

テトラ「$h$ の代わりに $d$ を使うということですか？」

僕「そうだね。距離を意味しているdistanceのことだと思うんだけど、 僕が重力場と電場を並べて考えたとき『これって《高さ》で考えた方がわかりやすいかも』と思ったんだ」

テトラ「なるほどです」