![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png)
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕：数学が好きな高校生。
テトラちゃん：僕の後輩。 好奇心旺盛で根気強い《元気少女》。言葉が大好き。
リサ：自在にプログラミングを行う無口な女子。赤い髪の《コンピュータ少女》。
双倉図書館の一般講座《リンクとストラクチャー》でアルゴリズムを学んできたテトラちゃんは、 自分の理解のため、学んだことを僕に向けて《講義》している。 僕たちは、線形リスト、双方向リスト、そしてスタックとキューについて議論してきた。
いまは階段教室で二分探索木の議論をしているところ（第327回参照）。
僕「テトラちゃんが書いてくれたSEARCH-SUBTREEの 再帰呼び出しについてはよくわかったと思うよ。 確かに《素直に読める》かもしれない」
テトラ「講師の先生は《再帰的な構造》と《再帰的なコード》が呼応しているとおっしゃっていました」
僕「構造とコード？」
テトラ「はい。二分探索木は《再帰的な構造》を持っています。 どういうことかというと、二分探索木の《根》となるノードはkeyというフィールドとleft, rightというフィールドを持ちます」
僕「そうだね」
テトラ「そしてleftとrightフィールドの先には、二分探索木の《根》となるノードがリンクされています。 言い換えますと、《二分探索木は二分探索木で作られている》ことになります。 《再帰的な構造》です！」
僕「自分自身を使って作っているからだね。なるほど」
テトラ「コード……つまりプログラムも同じように再帰的に作られています。 先ほど（第327回参照）のSEARCH-SUBTREEでは、 入力としてtとkが与えられていますよね。そして……」
僕「そうか。テトラ先生！ 僕が言ってもいいでしょうか？」
テトラ「はい、どうぞ！」
僕「SEARCH-SUBTREEには探索対象となる二分探索木の《根》がtとして与えられている。 そして、kの値の大きさに応じて、t.leftを探索対象にするか、t.rightを探索対象にするかを選んだ上でSEARCH-SUBTREEを呼び出している。 言い換えると、《SEARCH-SUBTREEはSEARCH-SUBTREEで作られている》ことになる。 《再帰的なコード》なんだね」
テトラ「そういうことですね。 《素直に読める》というのは決して感覚的なものではなくて、 構造とコードが呼応していることを意味しているんです！」
僕「おもしろい！ おもしろいなあ……」
テトラ「おもしろいですよね」
テトラ「……ところで先輩、 ここでクイズです！ どうしてわざわざ二分探索木などというものを考えるか、その理由はわかりますか？」
僕「理由……」
僕は考える。
そもそもノード同士をリンクを使ってつなぐというのは、 大量のデータを出し入れするときに、 メモリ上で動かさずにすむというメリットがあった。工学的理由ともいえる（第322回参照）。
二分探索木でもリンクを使っている。 でもここではまだ、データの出し入れについては何も考えていない。 単にキーの値を《探索》しているだけだ。
二分探索木を使うメリットが何か。大小比較で部分木を進んでいくメリット……
テトラ「いかがでしょう」
僕「改めて考えると難しいね。二分探索木を使うメリットが何かあるんだろうけど、 大小比較して探索していくというのは当たり前じゃないのかなあ？」
テトラ「存在するならば探索していけば見つかるから、大小比較して探索するのは当たり前ということですか？」
僕「そうそう」
テトラ「手間はいかがでしょう」
僕「手間？ ああ、そうか。 たぶん、わかったと思う。これは目的のキーが見つかるかどうかじゃなくて、 手間を掛けずにすばやく見つけられるかがポイントなんだね？」
テトラ「そうです！」
僕「二分探索木では、比較するたびに左部分木か右部分木かのどちらかに進んでいく。 目的のキーを順番に一つずつ探していく方法とは違って、 探す対象をすばやく絞り込んでいくことができるんだ」
リサ「リニアサーチとバイナリサーチ」
急にリサが声を出したので、僕たちはびっくりした。
リサがいることをすっかり忘れていた。
でもリサは解説を加えるでもなく、こちらを見もせずにタイプを続けている。彼女はタイピングも無音なのだ。
テトラ「……線形リストに10,20,30,40,50,60,70という7個の値があったとして、 もしも端から順番に探していく探索アルゴリズムである《リニアサーチ》を使うなら、 50を見つけるまでにノードを5個調べることになります」
線形リストの10,20,30,40,50,60,70から《リニアサーチ》で50を探索
僕「うん」
テトラ「でも、二分探索木を使った探索アルゴリズムである《バイナリサーチ》を使うなら、 Example Treeで50を見つけるまでにノードを3個調べるだけですみます」
Example Treeの10,20,30,40,50,60,70から《バイナリサーチ》で50を探索
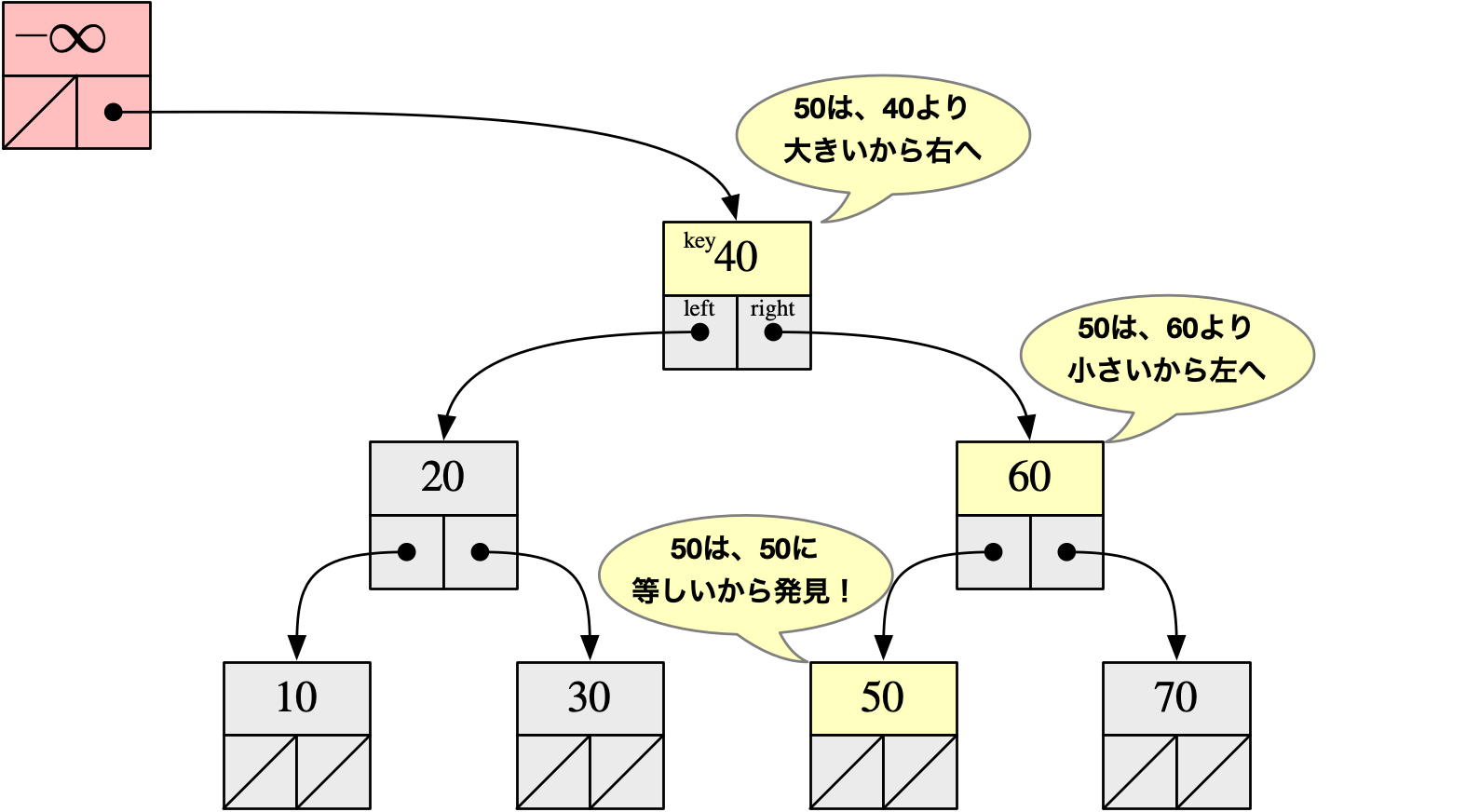
僕「……」
テトラ「50を見つける場合だけじゃありません。 《ノードを3個調べる》という手間をゆるすならば、 10,20,30,40,50,60,70という7個のキーのどれでも見つけることができますし、 もしもキーがExample Treeにないなら、それも調べることができます」
僕「……確かに、確かに」
テトラ「ここで、もしも」
僕「あー、ちょっと待って待ってテトラちゃん。そこから先は自分で考えたい！」
テトラ「あっ、あっ、はいはいっ！」
僕は、あわてて手を挙げてテトラちゃんの解説をストップしてもらった。
なるほどなあ……テトラちゃんはよく手を挙げて僕の説明をストップするけれど、 あの気持ちがよくわかる。
《先生》であるテトラちゃんに、どんどん先に話を進められても困る。
いくらおもしろい話だとしても、話をぜんぶ聞いてしまったらおもしろさは激減してしまう。 自分で考える楽しみが大きく損なわれてしまうからだ。
わかるにせよ、わからないにせよ、提示された情報を自分で吟味する時間がほしくなる。
そして、説明をいますぐストップしてほしい！と伝えるためには、即座のアクションが必要になる。
僕「……」
テトラ「……先輩？」
僕「うん。テトラちゃんは『《ノードを3個調べる》という手間をゆるすならば』と 言ったけど、調べるノードの個数を1個増やして、 《ノードを4個調べる》という手間をゆるすならば、 こんな二分探索木を作っておけば、15個のキーから見つけることができるよね」
テトラ「はい……その通りです。まさにその話をしようと思っていました……」
僕「そして、そこまで考えたら一般化できると思った。 こういう問題11が自然に浮かび上がる。 そして、これは、数列の漸化式（ぜんかしき）として考えられる！」
問題11（二分探索木）
二分探索木で《ノードをn個調べる》という手間をゆるしたときに、 最大でK(n)個のキーから正しく探索できるとする。
K(n)をnで表せ。
テトラ「はい、そうですね。これを解くのは難しくはありません。なぜなら……」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 440本すべての記事が読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方／すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加（2021年6月18日）
![[icon]](https://img.hyuki.net/20220619121014-abd58cfc2ab436f4.png)