![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。 好奇心旺盛で根気強い《元気少女》。言葉が大好き。
双倉図書館の一般講座《リンクとストラクチャー》でアルゴリズムを学んできたテトラちゃんは、 自分の理解のため、学んだことを僕に向けて《講義》している。
最大の値を求めるMAX-VALUEを題材にしたり(第321回参照)、 線形リストのノードを先頭に移動するMOVE-TO-FIRSTを題材にしたり(第322回参照)、 リストヘッド付き線形リストを議論したり(第323回参照)、 双方向リストを考えたり(第324回参照)と、いろんな議論を重ねてきた。
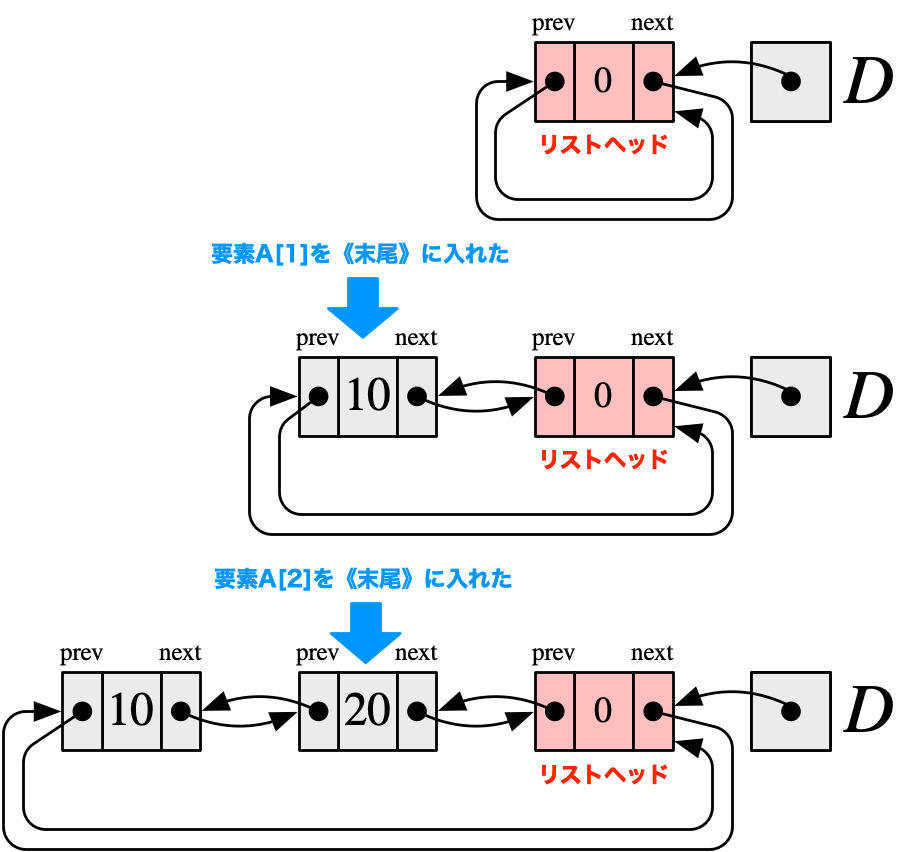
いまは、配列から双方向リストを作るプログラムを考えていて……
配列から双方向リストを作る(NEW-LIST-FROM-ARRAY)
与えられた配列の各要素を順番にノードに持つ双方向リストを得る。
入力
出力
NEW-LIST-FROM-ARRAYの実行例
テトラ「List 23にNEW-LIST-FROM-ARRAYの《まちがった実装例》があります」
僕「《まちがった実装例》って?」
テトラ「つまり、いわゆるバグのあるプログラムです。問題7の間違い探しをしてくださいっ!」
List 23 問題7(間違い探し)

僕「ええと……」
僕はList 23をていねいに読んでいく。
テトラちゃんの《講義》でわかったことがある。それは「簡単に見えるプログラムでも油断はできない」という当たり前の事実だ。
ほんのちょっとした違いでも、プログラムはおかしな動作をする。パパッと見て正確な動作を言い当てることは難しいし、 もしも思い込みがあったりしたらなおさらだ。
そして……うん、図を描こう。
テトラ「……」
僕「……」

テトラ「……い、いかがでしょう」
僕「うん、List 23の間違いはわかったと思う。 まず、基本的には、このNEW-LIST-FROM-ARRAYは動くよね。 といってもそれは『少なくとも配列から双方向リストを作ってはいる』という意味だけど、双方向リストじゃない変なものができるわけじゃない」
テトラ「はいはいっ!」
僕「List 23の行番号でいうと、A2でリストヘッドを作る。これは、要素が0個の双方向リストといえる。 その後、A3からA11までのwhileの繰り返しで、 $$ A[1], A[2], A[3], \ldots, A[n] $$ という値を双方向リストに順番に挿入している……繰り返しのたびに $k$ が増えていく。1からnまで順番に」
テトラ「はい……」
僕「それで、A6からA9のリンクの付け替えは、これまでに練習したものと同じだから間違いはないんだけど、 重大な間違いがある。このList 23のままだと『配列の要素が逆順になった双方向リスト』になってしまう。 そこが間違いだね!」
テトラ「はいっ、そうです。そこが間違いになります。先輩、大正解ですっ!」
テトラちゃんは、うれしそうに拍手してそう言った。
その瞬間、僕の心に深い喜びがやってきた。
新鮮な感覚だ。間違い探しで正解を出したことは、 それだけでもちろんうれしいんだけど、 こんなふうに拍手されるなんて、これまであっただろうか。
小学生のころなら、もしかしたらあったかもしれないけれど……
僕「……」
テトラ「正解です……よ?」
僕「あ、うん。いや、ありがとう、テトラちゃん」
テトラ「は、はあ」
僕「List 23の間違い探しがちょっと難しいのは、 与えられた配列の要素が一個の場合、つまり $n = 1$ の場合には間違いに気付かない点だね」
テトラ「そうですね。要素が一個なら、逆順になってもわかりませんから」
僕「僕は、 $$ A[1] = 10,\, A[2] = 20,\, n = 2 $$ を使って、10と20を順番に入れようとしたところで気付いたよ。A6からA9は、 pが指している新たなノードを双方向リストDの《先頭》……つまりリストヘッドの次に入れる処理だから、 毎回《先頭》に入れていったら逆順になっちゃうんだね」
10と20を順番に《先頭》に入れると逆順になる

テトラ「先輩ならどう修正なさいますか?」
僕「うん。確保したノードを双方リストの《末尾》に入れればいいね。それには、A6からA9のnextとprevをすべて逆にすればいい!」
List 24 解答7
List 23のままでは、与えられた配列の要素が逆順になった双方向リストになってしまうので、以下のように修正する。

10と20を順番に《末尾》に入れると正しい順番になる
テトラ「はい、List 24のようにしてもいいですし、List 25のように配列の要素を逆順に入れるという手もあります」
List 25 解答7a(別解)

僕「なるほど。nextとprevはList 23のままにしておいて、 $k$ をnから1まで減らしていくんだね。確かに同じことだ」
テトラ「NEW-LIST-FROM-ARRAY以外にも、まだまだ問題はあります。次はどんな問題がお好みでしょうか?」
僕「そうだなあ……リンクの付け替えでいろんなことができるのはわかってきたんだけど、 これっていったんどんなふうに役立つんだろうね」
テトラ「So what?(だから、何?)ですねっ!」
僕「ああ、確かに。テトラちゃんが出してくる《根源的な質問》に近いかも。 根源的というよりも応用的かもしれないけど……」
テトラ「それでは、こんな問題はいかがでしょう!」
問題8(カッコの対応)
与えられた《文字列》に現れる「カッコ」が正しく対応しているかどうかを調べるアルゴリズムMATCHEDを考えてください。
入力
出力
文字を読む方法
NEXT-CHARACTERという手続きを使い、以下のようにしてファイルの先頭から一文字ずつ文字を読んでいくことができます。 $$ c \leftarrow \textrm{NEXT-CHARACTER}(f) $$ もしも文字をすべて読み尽くしていたならば、終端を表す特殊な文字が得られます。
それから……
僕「カッコの対応を調べるアルゴリズム……なるほどね。たとえば、 $$ (1 + 2) $$ のようになっていたら正しい対応になっていて、 $$ (1 + 2 $$ だったら正しくない対応という意味かな? そんなに難しくなさそう」
テトラ「それだけじゃなくてですね……」
僕「ああ、そうか。複数個あるのか! たとえば、 $$ ((1 + 2) + 3) $$ のようになる場合があるんだね。だとすると……」
テトラ「ええ、そうなんですが……」
僕「うん、簡単だね。開きカッコの個数を数えるだけで済む」
テトラ「……といいますと?」
僕「開きカッコの個数と、閉じカッコの個数が等しくなればいいよね。 まだ閉じていない開きカッコの個数を、最初は0にしておいて、 読んだ文字が開きカッコだったら1増やして、閉じカッコが来たら1減らす。 文字を読み終えたとき、閉じていない開きカッコの個数が0になっていたら正しいカッコの対応だ」
テトラ「先輩、先輩! 問題は最後まで聞いてくださいっ!」
僕「……はい。すみません」
反省。
これじゃ僕はまるで、はしゃいでいる小学生だな。テトラ先生に「めっ」と怒られそうだ……
テトラ「先輩のおっしゃる《開きカッコの個数を数える》方法ではまずいことが起きます。 たとえば、 $$ ))1 + 2(( $$ という文字列が与えられた場合でも、 文字を読み終えたときには閉じていない開きカッコの個数は0ですよね。 でもこれは、正しいカッコの対応とはいえません」
僕「確かに。文字を読んでいる途中で負になってはいけないという条件が必要だね」
テトラ「それに、カッコは一種類とは限りません。たとえば、 $$ [ \{1 + 2\} + (3 - 4) ] $$ のようになっていても、正しいカッコの対応であると見なすことにします。 でも、 $$ [ ( 1 + \{ 2 + 3 ) - 4 \} ] $$ は正しいカッコの対応とは見なさないことにします。正しい入れ子になっていないからです」
僕「なるほど……だとすると、カッコの種類ごとに数を数える必要があるか。いや、待てよ……」
テトラ「問題8を改めて示しますね」
問題8(カッコの対応)
与えられた《文字列》に現れる「カッコ」が正しく対応しているかどうかを調べるアルゴリズムMATCHEDを考えてください。
入力
出力
文字を読む方法
NEXT-CHARACTERという手続きを使い、以下のようにしてファイルの先頭から一文字ずつ文字を読んでいくことができます。 $$ c \leftarrow \textrm{NEXT-CHARACTER}(f) $$ もしも文字をすべて読み尽くしていたならば、終端を表す特殊な文字が得られます。
文字を調べる方法
MATCHEDは、どんなときに何を返すか

無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2021年5月28日)