![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。 好奇心旺盛で根気強い《元気少女》。言葉が大好き。
いまは放課後。ここは高校の図書室。
僕と後輩のテトラちゃんは、村木先生から渡された問題を解いていた。
一つ目の封筒に入っていた問題をようやく解いたところ。(第293回参照)
ようやく解いた……といっても、問題を作ったのは僕たちなんだけどね。
テトラ「できましたね…… それにしても、《小さな数で試してみる》ってどうしてこんなに効果的なんでしょう」
僕「どうしてだろうね。小さな数で試しているうちに、その問題のことをよく理解するからかなあ……」
テトラ「あたし、一気に一般の $n$ に挑戦する癖を何とかやめたいです。一度にすべてを解く!とか、いっぺんに全部を理解する!のに憧れちゃうんでしょうか……」
僕「一歩ずつ、だよね」
テトラ「一歩ずつ……あっ、そういえば! 封筒はもう一個あるんでした。いっぺんに開けないでと村木先生はおっしゃっていましたけど、 もういいですよね」
僕「ああ、そうだね。こっちにはどんな問題が入っているんだろう」

僕とテトラちゃんは残っていたもう一つの封筒を開けた。
中には……
テトラ「何でしょう。これは、ビニール?」
僕「ビニールというか、クリアファイルかな。いやファイルじゃない。二つ折りになったシート? 透明なシートっぽいね」
テトラ「図が描いてあります……ボードゲームみたいですね」
二つ目の封筒に入っていた透明シート
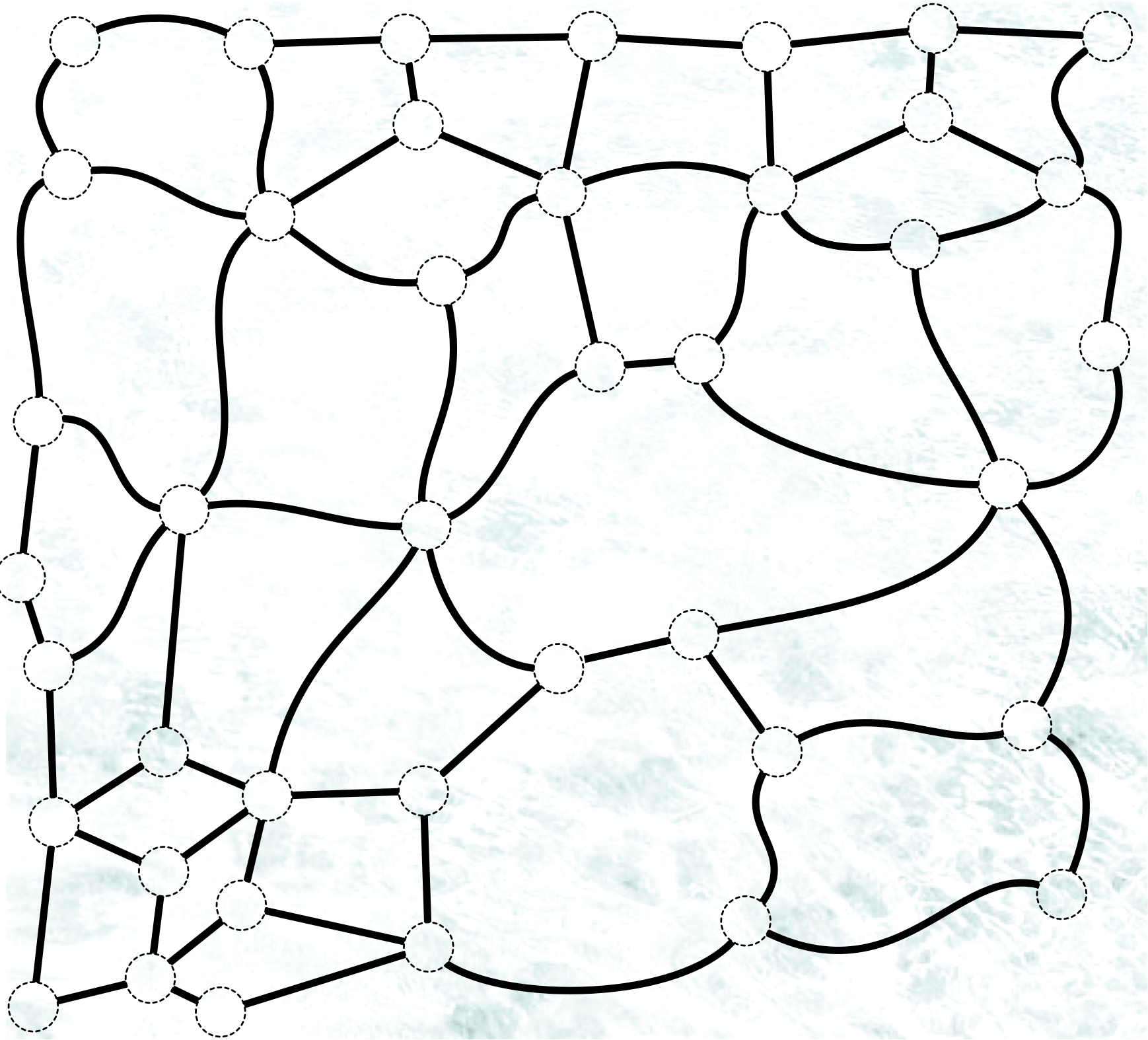
僕「僕には何かの《配線図》みたいに見えるなあ。こっちも図形問題なのかな。 一つ目の封筒には古い紙を使った《地図》が入っていて、 二つ目の封筒には透明シートを使った《配線図》が入ってる……と」
テトラ「古い紙と透明シート……もしかして、過去と未来の演出ということでしょうか。時を越える演出とか?」
僕「演出はさておき、肝心の《カード》は入っているかな」
テトラ「《カード》もありますね。あ、あちゃちゃ?!」

テトラちゃんが《カード》を取り出そうと封筒を逆さにして振ると、 《カード》といっしょに小さくて薄いプラスチック片がパラパラと落ちてきた。
僕「これはオセロの石みたいだね。ずいぶん小さいけれど……」
テトラ「封筒の中でシャカシャカ音がしてたのは、これだったんですね」
僕「とにかく《カード》の方を読もうよ」
二つ目の封筒に入っていた《カード》
この図は、未来都市の施設内に作られた通信網である。
小さな丸印はセンサーを配置するための場所を表し、 二つの丸印をつなぐ線はセンサー間で通信が可能であることを表している。
センサーを表している小さな丸印を《頂点》と呼び、二頂点を結ぶ線を《辺》と呼ぶことにする。
センサーには「白」と「黒」の二種類が存在し、すべての頂点にどちらか一種類のセンサーを配置しなければならない。
ただし、一つの辺の両端には白と黒の両方を配置しなければならない。
テトラ「《頂点》は、このシートの丸印で、《辺》は頂点を結んでいる線のことですね」

僕「そうだね……そして頂点に、白と黒のセンサーを置く。 さっき落ちてきたオセロの石のどちらかを上にして、頂点に置くってことか……なるほど」
テトラ「どういうゲームなんでしょう」
僕「いや、ゲームなのかな……この《カード》の説明だと、単に白と黒を置いてぜんぶを埋めればいいんだと思うよ。 ああ、でも、ルールが一つあったね」
テトラ「はい。これですね。『ただし……』」
ただし、一つの辺の両端には白と黒の両方を配置しなければならない。
僕「そうだね。だから、たとえば白と黒は、こんなふうに置かなきゃいけないんだ」
一つの辺の両端には白と黒の両方を配置しなければならないというルールを守った例

テトラ「はい、わかります。 それから、たとえばこんなふうに黒を二つ、隣り合うように並べてはいけないんですね。 でも、これは難しいことじゃありませんよ。 だって、同じ色が並ぶかどうかは見ればすぐにわかりますから」
一つの辺の両端には白と黒の両方を配置しなければならないというルールを破った例(黒が並んでいる)
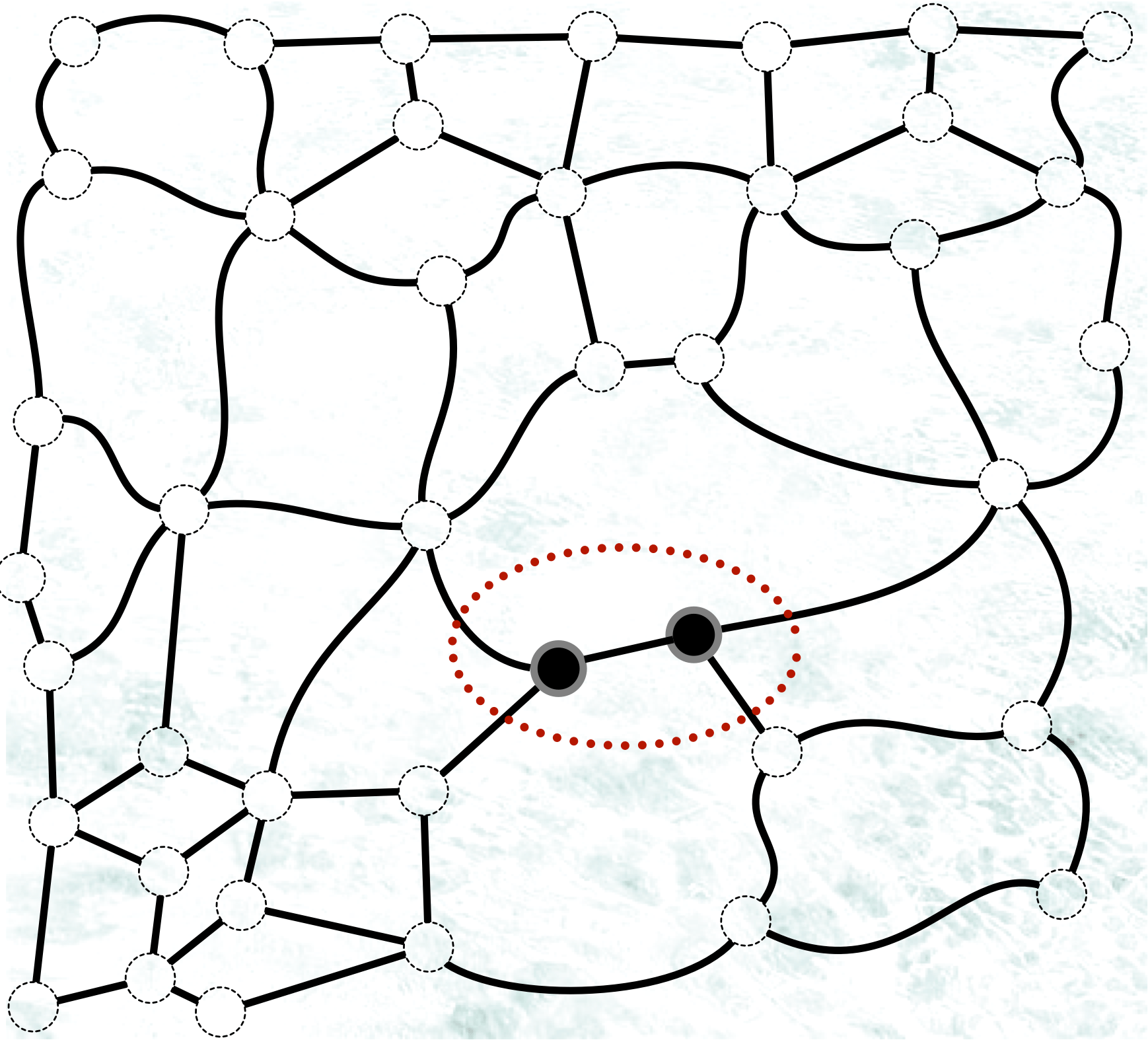
僕「まあね。でも、頂点はけっこう多いよ」
テトラ「大丈夫です! 二人で分担すれば、すぐですっ! 何ならあたし一人でもっ!」
僕「ともかく置いてみようか」
僕とテトラちゃんは白と黒をシートの《頂点》に置いていく。
もちろん、《辺》の両端は違う色になるように注意しながら……
テトラ「あっ、先輩。だめです。そこは白を置く頂点ですよ」
僕「え、でも、ここは黒になる頂点なんだけど……僕の側から見ると」
テトラ「え、ええっと……あたしの側から見ると白なんです」
白も黒も置けない場所がある?!
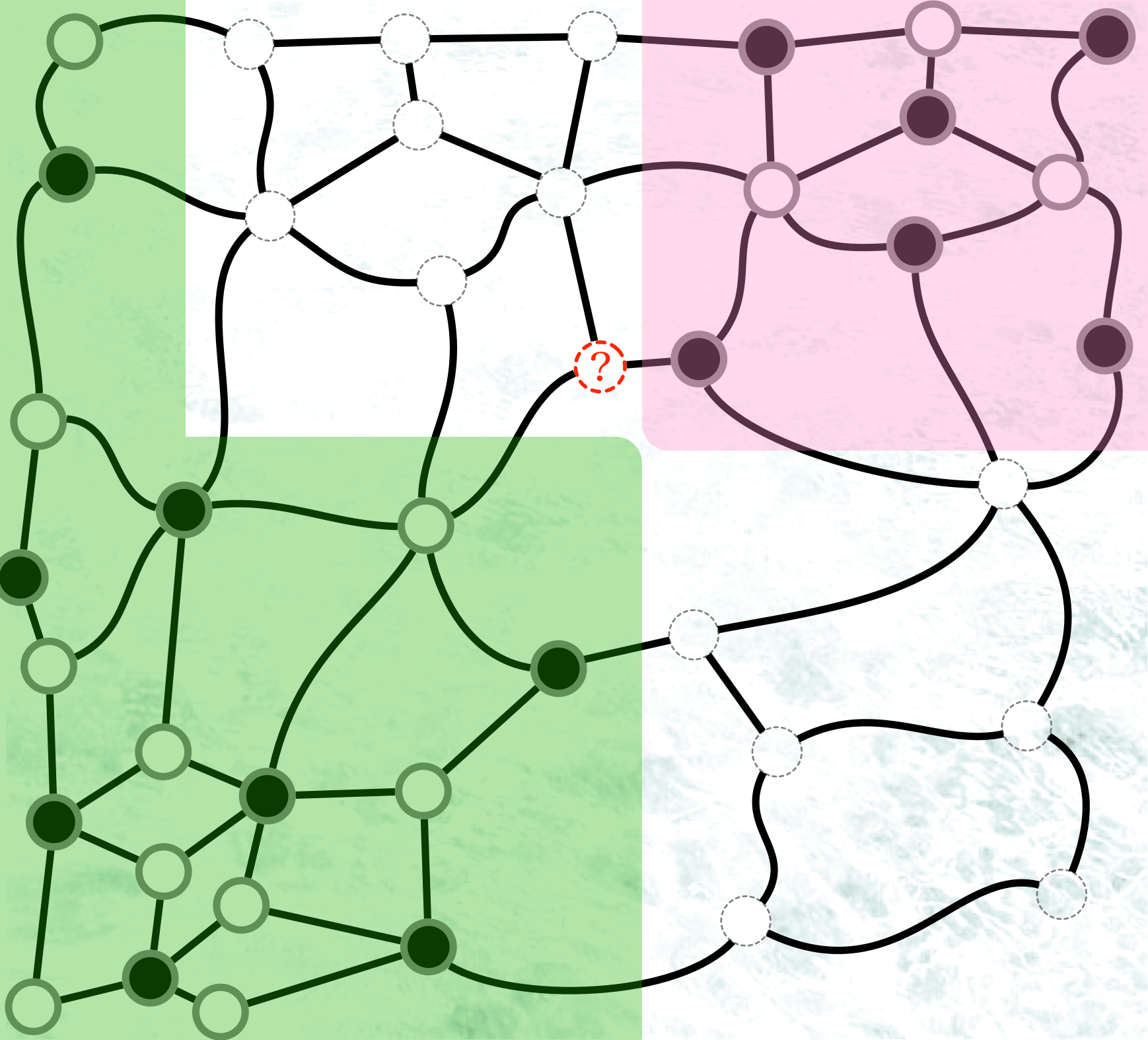
(テトラちゃんは右上から、僕は左下から置いていった)
僕「……僕たちは、かなり間抜けなことをやっちゃったみたいだね」
テトラ「もしかして、このゲーム、二手に分かれてはまずかった……?」
僕「そういうことになりそうだね。僕とテトラちゃんが別の場所から置き始めたから、ぶつかってしまったんだ」
テトラ「あっ、でも、たいした手間じゃありませんから、あたしのを全部やり直せばいいですよ。ぜんぶいったん片付けて……」
僕「ああああああっ、ストップストップ!」
テトラ「せせせ先輩っ!」
僕「ごめん! つい……痛くなかった?」
僕は、オセロの石を片付けようとしたテトラちゃんの手を思わずつかんでしまった。
テトラ「だだだ大丈夫です。びっくりしただけです」
僕「ごめんね。あのね、片付けるんじゃなくて、色を反転させればいいんじゃないかと思ったんだよ」
テトラ「え? ああ……そうですね」
テトラちゃんはいったん置いた石をすべて反転した。
テトラちゃんが置いた石をすべて反転させた

僕「そうそう。《辺の両端を違う色にする》というのがルールだから、ルールを守っている範囲を反転しても、やっぱりルールは守っていることになる」
テトラ「これで、さっき《ごっつんこ》したところは、黒に決まります」
僕「あれ……?」
ルールを守り、頂点をすべて埋めた

テトラ「はい、残りもぜんぶ埋めちゃいましたよ! これで完成です。簡単な問題でしたね」
僕「……」
テトラ「先輩?」
僕「ねえ、テトラちゃん。これって同じ問題だよね」
テトラ「何がですか?」
僕「村木先生からの二つの封筒。その中身は同じ問題に見えるんだけど!」
テトラ「……確かに、二つの色で塗り分けるという点では同じですが?」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2020年6月26日)