![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
僕はユーリといっしょに《音楽と数学》というイベントに来ている。
いまは《音は波》というコーナーを回っているところ(第281回参照)。
ユーリ「お兄ちゃん、次のパネルに行こうよ」
僕「さっきから会場を走り回ってるから、《次》がどこかはもうわからないよ」
ユーリ「いーの、いーの。新しいパネルに行けばそれが《次》だもん」
僕「はいはい」
クイズ(音の大きさ)
(X)(Y)(Z)は、音をグラフとして表したものです。
最も大きい音はどれでしょうか。また最も小さい音はどれでしょうか。
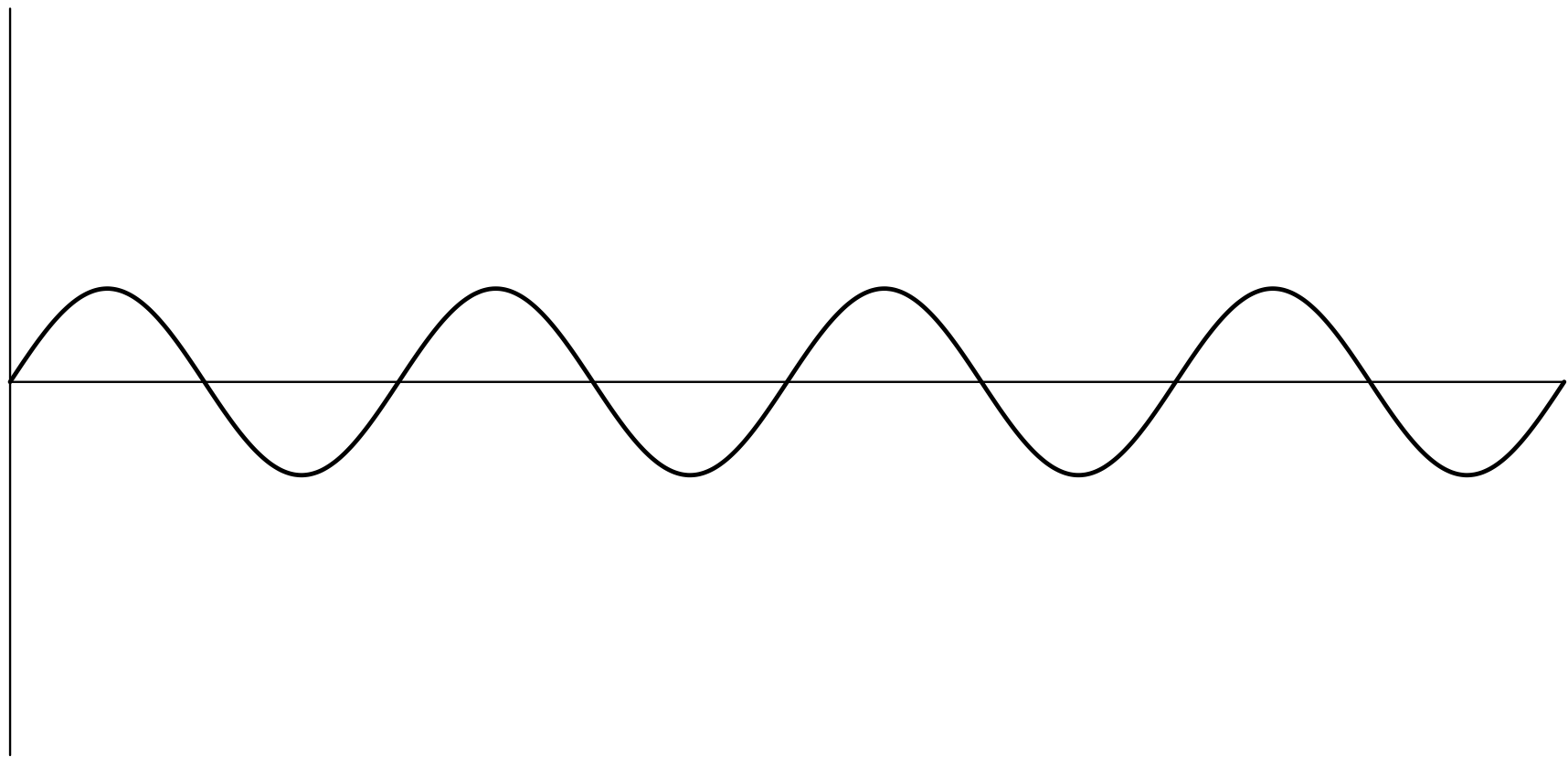
(X)
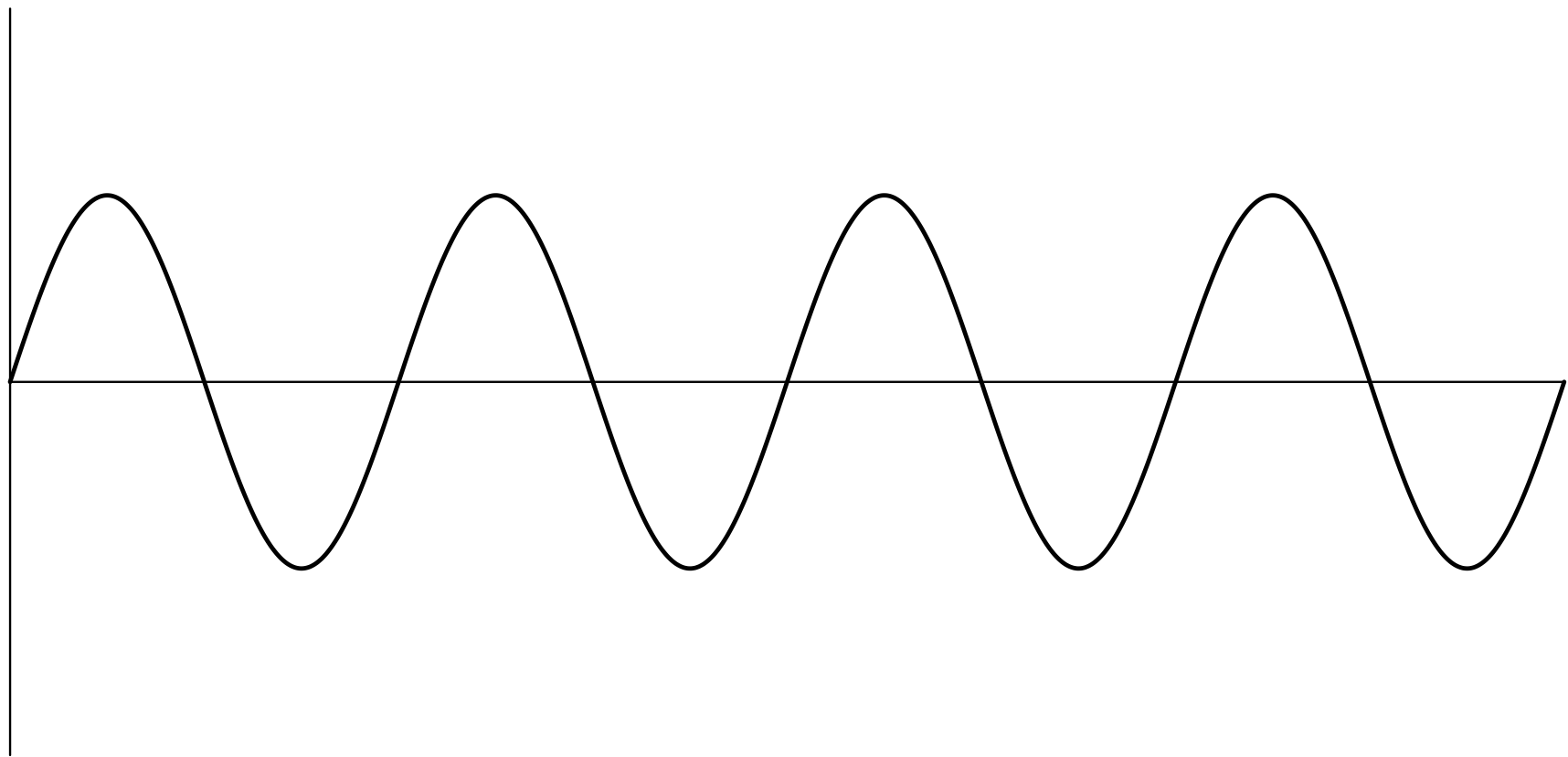
(Y)
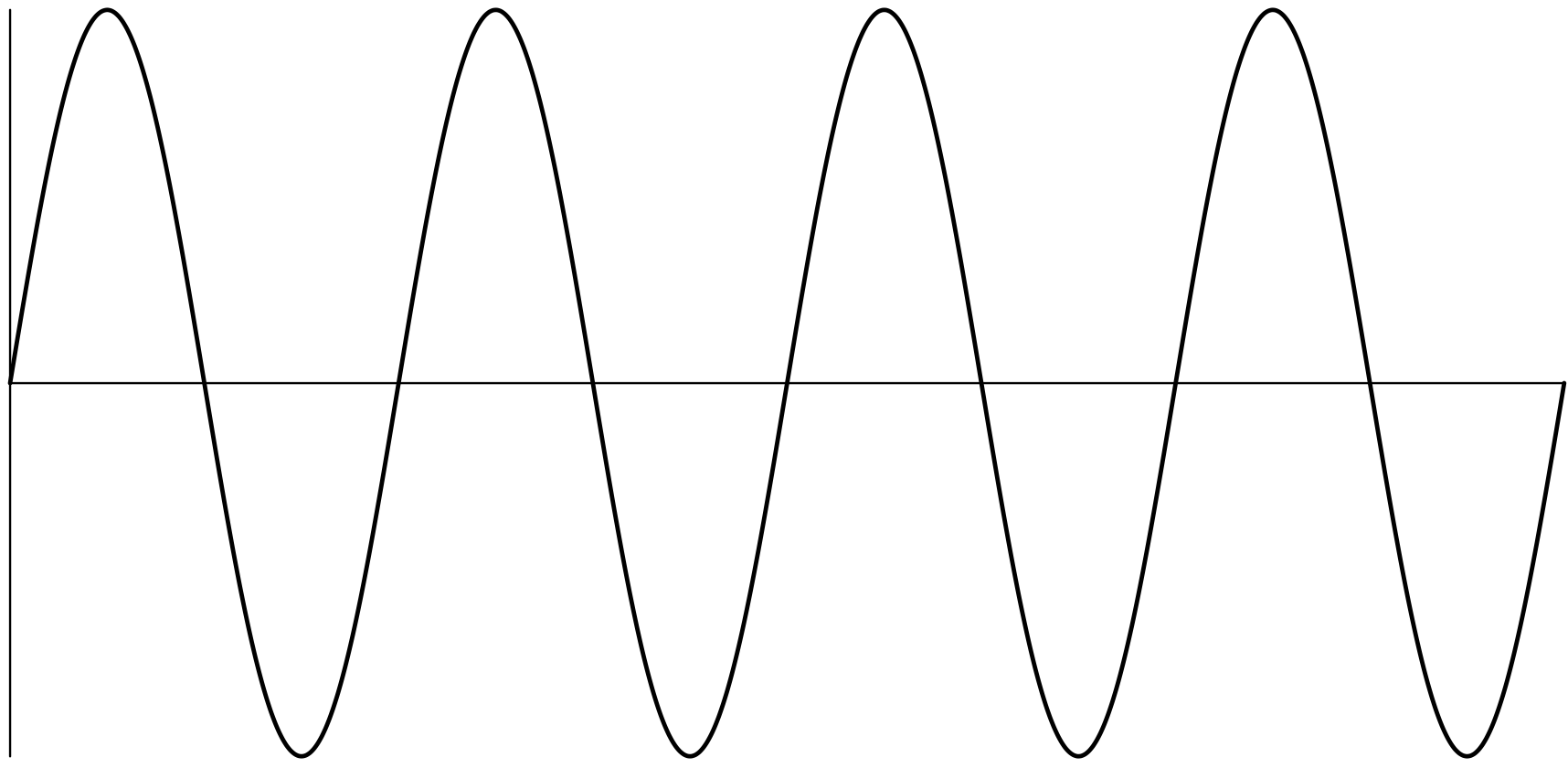
(Z)
※横軸は時刻を表し、縦軸は音圧を表しています。またグラフはどれも同じスケールとします。
ユーリ「あ、これはさっき見たクイズパネルだっけ?」
僕「見てないね。さっき見たのは《音の高さ》のクイズパネルだけど、このクイズパネルは《音の大きさ》だから(第281回参照)」
ユーリ「そっか。音がいちばん大きいのは(Y)だよね。それからいちばん小さいのは(Z)」
僕「そうだね。正解」
クイズの答え(音の大きさ)
(X)(Y)(Z)は、音をグラフとして表したものです。
最も大きい音は(Y)で、最も小さい音は(Z)です。
(X)

(Y)

(Z)

※横軸は時刻を表し、縦軸は音圧を表しています。またグラフはどれも同じスケールとします。
ユーリ「カンタン!」
僕「このグラフでは、音の大きさは《波の振幅》の大きさとして表されていることになるね。ここの部分」
波の振幅

ユーリ「カンタンなクイズばっかりだね」
僕「《音は波》のコーナーは、音が波であることや、波の要素について親しんでもらおうというコーナーだからじゃないかな。 親しんでもらうのに、超難問でいきなり挑戦してもしょうがないよね」
ユーリ「その方が楽しそう! 超難問大好きだぜ!」
僕「いやいや」
ユーリ「……波の要素って何?」
僕「波を特徴付けているものは何かということだよ」
ユーリ「また、難しい話を始めたね?」
僕「超難問、好きなんだろ?」
ユーリ「またそーゆーこと言う」
僕「波を特徴付けているものっていうのは、波の周波数や、波の波長や、波の振幅などだよ。そのほかには……」
ユーリ「波を特徴付けているものって大事なの?」
僕「そりゃ大事だね。 《音は波》だから、《波を研究する》のは《音を研究する》ことに関係してくる。 じゃ、《波を研究する》っていうのは、いったい何をすることなんだろうか」
ユーリ「ほほー?」
僕「たとえば『ああ……音が鳴ってるなあ……ああ……音が聞こえるなあ……』と何となくぼんやり考えるだけだと話は進まないし、きちんと考えられない」
ユーリ「ちょっとぼんやりし過ぎじゃね?」
僕「『この音は高いけれど、あの音は低い』や『さっきの音は小さいけれど、いまの音は大きい』みたいに、音が持っている特徴を注意深く見分ける必要がある」
ユーリ「聞き分ける」
僕「……音が持っている特徴を聞き分けて、音を見分けて、どんな音なのかを表現したくなる。 そしてそのために言葉が必要になる。音の高さを波の周波数として表したり、音の大きさを波の振幅として表したりして」
ユーリ「あっ!」
僕「わっ! ……急に大声出すなよ」
ユーリ「その話ってさー、お兄ちゃんがよく言う《二つの世界》の話だよね」
僕「そうかな?」
ユーリ「《音の世界》と《波の世界》の関係の話でしょ?」
僕「おお、確かに! ユーリ、賢いなあ!」
ユーリ「へへへ」
僕「いま言いたかったのは確かにそれだよ。 《音の世界》には、高い音や低い音、大きい音や小さい音がある。 それらの概念を《波の世界》に持っていくと、周波数が高い波や低い波、振幅が大きい波や小さい波に対応して……」
ユーリ「《がいねん》って何?」
僕「概念とは何か? また難しい質問してきたな。 ええと、概念とは、具体的な個々の対象を抽象化してまとめてとらえた……そういう概念。 いや、概念を定義するのに概念を使っちゃだめだな。ええと……」
ユーリ「無理しなくていーよ。さっきの話を続けたまえ」
僕「それで……《音の世界》には《高い音や低い音》《大きい音や小さい音》がある。 それらの概念を《波の世界》に持っていくと《周波数が高い波や低い波》《振幅が大きい波や小さい波》に対応する。 そうすると、別の観点から研究できることになる」
ユーリ「別の観点?」
僕「音が高い低いという《定性的》な話だけじゃなくて、周波数を使って《定量的》な話ができるということ。あ、定性的っていうのは」
ユーリ「てーせーてき、てーりょーてきは知ってる。お兄ちゃん教えてくれたじゃん」
僕「そうだっけ」
ユーリ「《どんな性質を持ってるか》ってゆーのが定性的で、《どのくらいの量か》ってゆーのが定量的でしょ。性質と量」
僕「そうそう! 《波の世界》の言葉を使って定量的に音の概念を表現すると、 音が高い低いだけじゃなくて、どのくらい音が高いかを表現できることになる。周波数を使えばいいからね。 人間の可聴域が約 $20$ Hz〜約 $20000$ Hzだという話があったけど、 それはまさに《音の世界》の概念を《波の世界》の言葉を使って表現した例になっている(第281回参照)。 人間の耳で聞こえる範囲という《音の世界》の概念を《波の世界》の言葉を使って定量的に表現していることになるわけだ」
ユーリ「うっわー……その話、理屈っぽいけど、おもしろーい!」
僕「そろそろ次のクイズパネルに行こうか」
ユーリ「うんっ!」
僕「これもクイズパネルかな」
ユーリ「どらどら」
クイズ(音の変換)
次の図は、 コンピュータのあるプログラムが音を変換しているところを表しています。
どのような変換であるかは、入力と出力の波で示されています。
入力した音に比べて、出力した音はどのように聞こえるでしょうか。
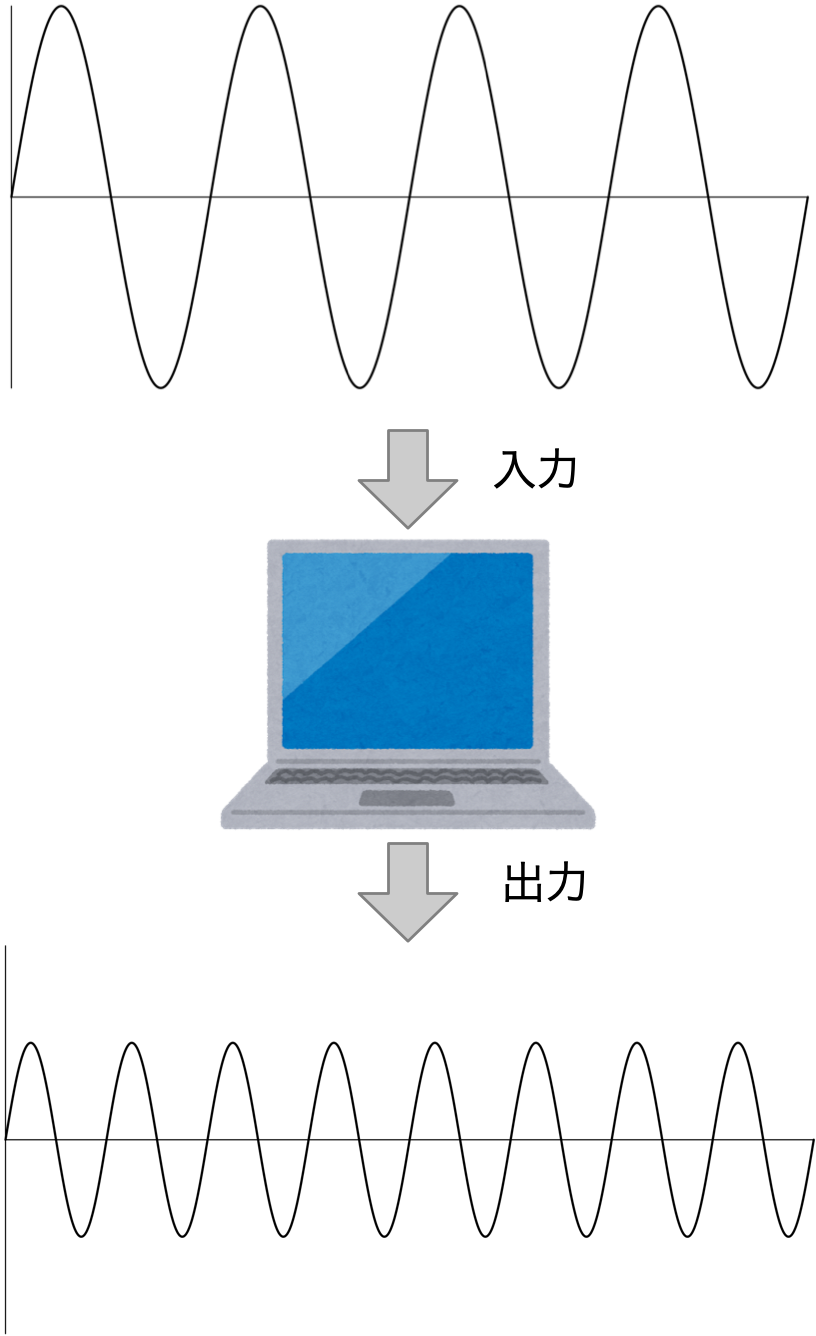
※横軸は時刻を表し、縦軸は音圧を表しています。またグラフはどれも同じスケールとします。
僕「なるほどね。音は波だから、その波の形をコンピュータで変換したら音はどうなるかという問題なんだね。 入力した音の波と、出力した音の波があるから、それを見比べて音がどう変わったかを答えるクイズ」
ユーリ「あー、これもカンタンカンタン。だってほら、さっきやったばっかじゃん。 入力に比べて出力は振幅が小さくなってる。だから、これ、音が小さくなる!」
僕「そうかな?」
ユーリ「え? ……あー、いまのなし! 音が小さくなるだけじゃないね……音が高くなってる?」
僕「そうだね。振幅を見て音の大きさを調べ、周波数を見て音の高さを見ることになる。 周波数は単位時間の波の個数で、出力の波の個数が多いから、音は高くなってる」
クイズ(音の変換)
入力した音に比べると、出力した音の大きさは小さく、音の高さは高くなります。

※横軸は時刻を表し、縦軸は音圧を表しています。またグラフはどれも同じスケールとします。
ユーリ「ははーん、これ、逆だね!」
僕「逆とは」
ユーリ「さっきと逆じゃん? さっきは《音の世界》を《波の世界》に移して定量的に考えるって話だったけど、 この音の変換は逆。《波の世界》の振幅や周波数を調べて、それで《音の世界》のことを考えてる」
僕「うーん、なるほど。ユーリ、今日は冴えてるなあ!」
ユーリ「今日も」
僕「ユーリ、今日も冴えてるなあ」
ユーリ「そんじゃ、次のパネルに行こー!」
僕「ちょっと待って」
ユーリ「え? まだ何か考える必要あるの?」
僕「うん。このクイズに出てきた入力と出力で気になることがある。 もしも、このコンピュータに向かって『人間が歌ったらどうなるか』って考えていたんだよ」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2020年1月31日)