![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
僕は高校生。今日は中学生のいとこ、ユーリといっしょに双倉図書館(ならびくらとしょかん)で開催されているイベントにやってきた。
イベントは《音楽と数学》という一般向け企画で、 音楽と数学の関わりについてパネル展示がなされている。 でも、単なる展示ではなくあちこちにクイズや体験コーナーもあるらしい。
一般向け企画だから、双倉図書館はいつもよりずっと人が多い。
もちろん、ミルカさんやテトラちゃんもいっしょに来ているのだが……
ユーリ「お兄ちゃん、早く早く! たっくさんパネルがあるから、全部まわるのに時間足りなくなるよ! ほら、は・や・く!」
僕「ちょっと待った、ユーリ」
ユーリ「あっ、スタンプラリーのシートもらって来る!」
僕「おいおい」
ユーリはインフォメーションにさっと走る。
いつもに増してはしゃいでいるなあ。
ユーリ「はい、これお兄ちゃんの分。会場にクイズパネルがあって、挑戦したらスタンプもらえるんだって!」
僕「ユーリ、ミルカさんやテトラちゃんとはぐれてしまったじゃないか。いったんエントランスまで戻ろうよ」
ユーリ「だーいじょぶだって。またすぐ会えるって」
僕「何だかこの会話、既視感あるぞ……前も同じようなことあったよね」
ユーリ「そーだっけ」
僕「そうだよ。同じこと繰り返してる。ユーリはいつもパッと先に行動するからなあ。いったりきたりしているうちに他のみんなとはぐれちゃうんだよ」
ユーリ「だってお兄ちゃんたち、歩くの遅いじゃん! 早く見たいのに! それより、ねーねー、どれから見る?」
僕「順番に見ていけばいいんじゃない? ええと、ここは《音は波》のコーナーだなあ」
僕とユーリは《音は波》と掲示されている部屋に入っていった。
ユーリ「ほらほら、お兄ちゃん。あそこにさっそくクイズパネルがある!」
クイズ(音の高さ)
(A)(B)(C)は、音をグラフとして表したものです。
最も高い音はどれでしょうか。また最も低い音はどれでしょうか。
(A)
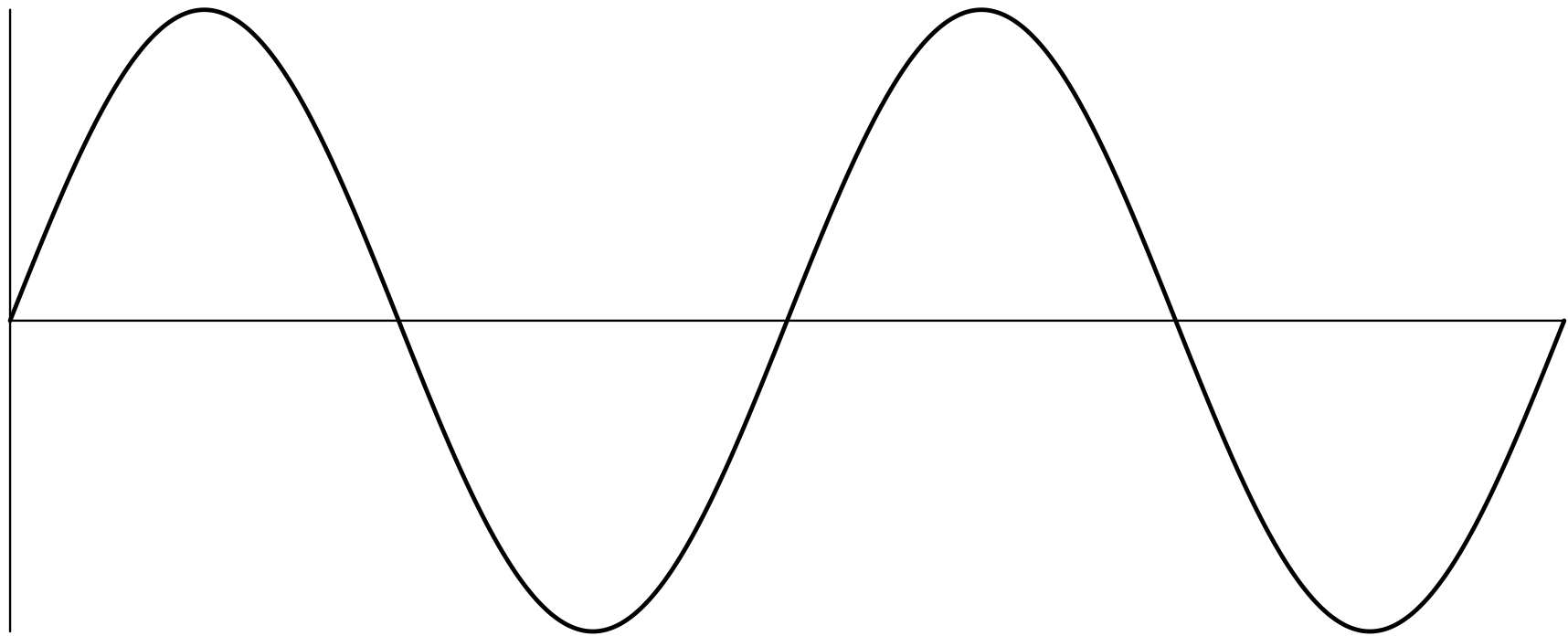
(B)
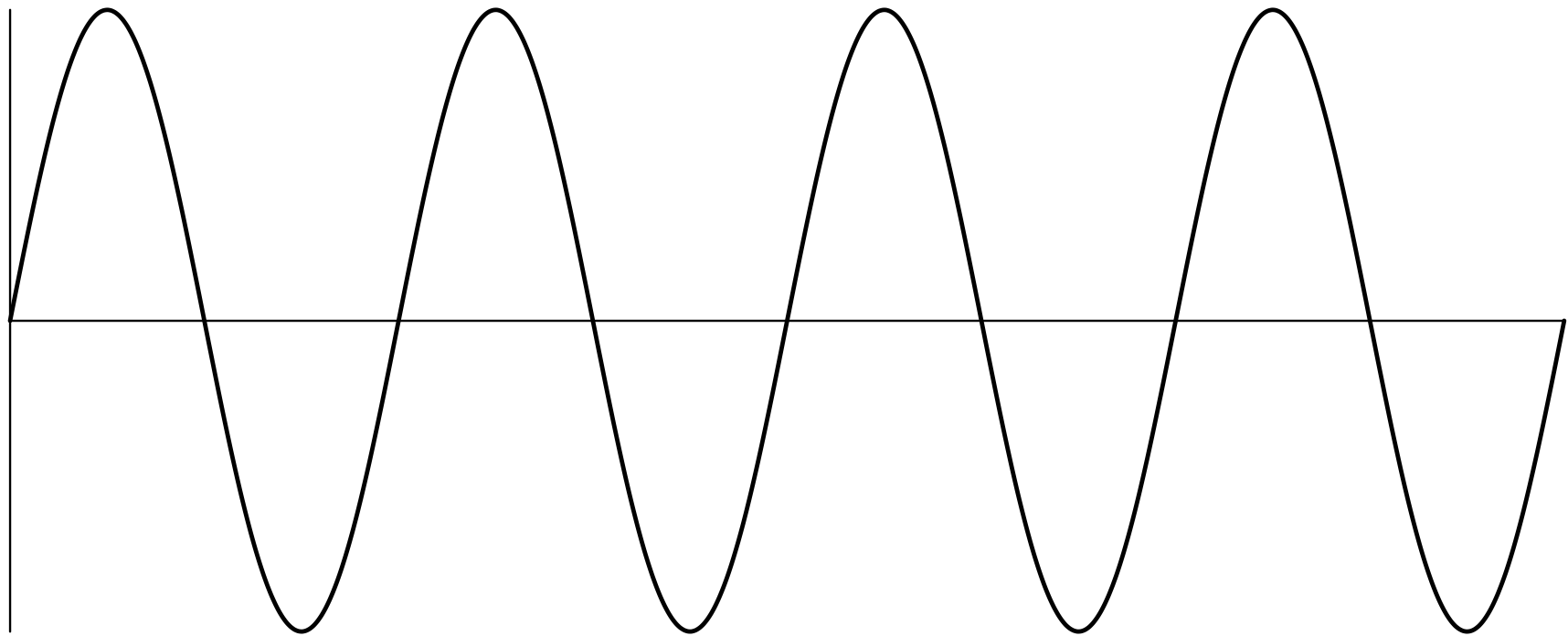
(C)
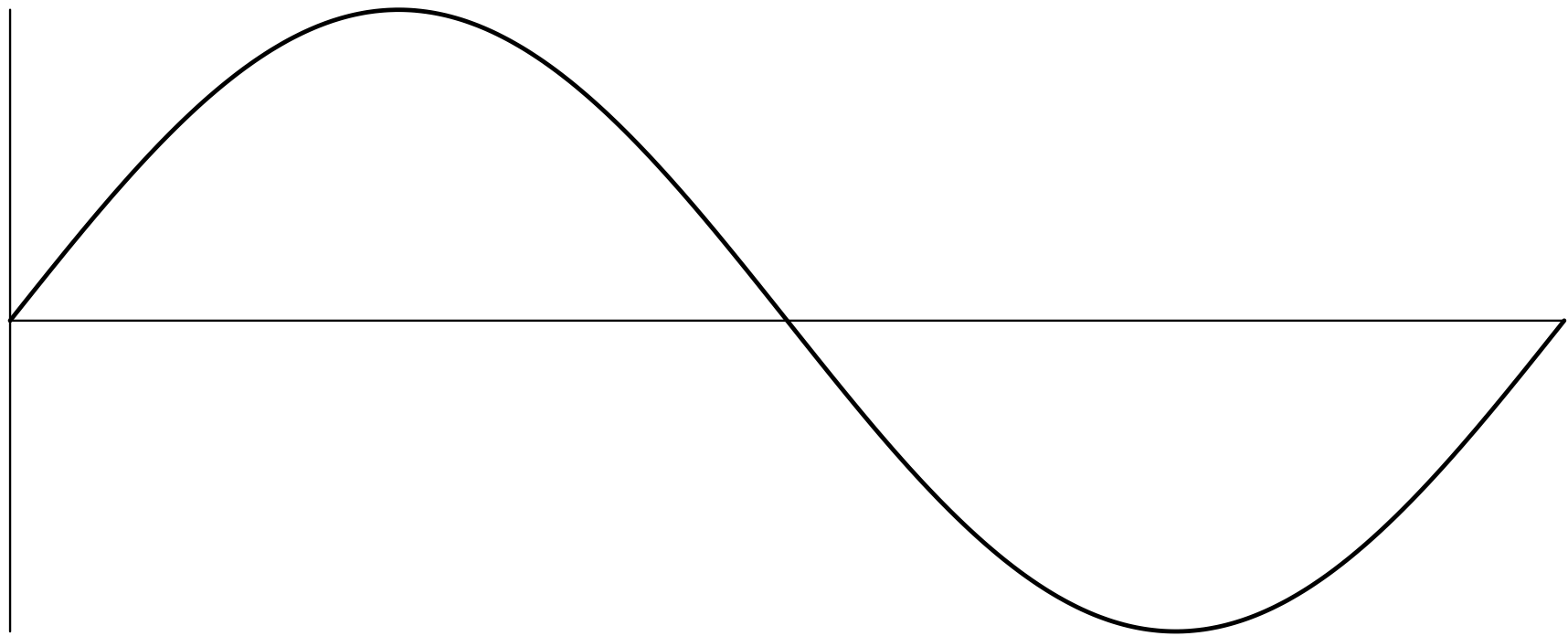
※横軸は時刻を表し、縦軸は音圧を表しています。またグラフはどれも同じスケールとします。
僕「なるほど」
ユーリ「これはわかる! カンタンだよ!」
僕「そうだね」
ユーリ「一番高い音は(B)で、一番低い音は(C)でしょ?」
僕「うん、それで正解」
クイズの答え(音の高さ)
(A)(B)(C)は、音をグラフとして表したものです。
最も高い音は(B)で、最も低い音は(C)です。
(A)

(B)

(C)

※横軸は時刻を表し、縦軸は音圧を表しています。またグラフはどれも同じスケールとします。
ユーリ「じゃ、スタンプ押して……っと、次のパネル!」
僕「ちょっと待って、ユーリ。(B)が最も高い音で(C)が最も低い音だというのはどうしてか、わかる?」
ユーリ「え、そんなのいーじゃん。次行こうよ、次。せっかく来たんだから、どんどん行こ!」
僕「せっかく来たんだから、ちゃんと考えていこうよ。《どうして》と考えようよ」
ユーリ「真面目かいっ! 《どうして大好き高校生》め!」
僕「謎概念を作るなよ」
ユーリ「……えーとね。 (A)よりも(B)の方が細かくて、たくさんくしゃくしゃ!ってなっているから高い音。 (A)よりも(C)は一番……一番広いから? 何ていえばいーの?」
僕「そこだよ」
ユーリ「?」
僕「グラフをパッと見たら、どれが高い音でどれが低い音かはすぐわかるよね」
ユーリ「カンタン。見ればわかる」
僕「そうだね。でも、その理由を言葉で説明するのは意外に難しい。 それはなぜかというと《それ》を表す単語を持っていないから。 単語を持っていないと《それ》をうまく指し示すことができず、理由をうまく説明できない」
ユーリ「いきなり、ややこしーこと言い出したね?」
僕「ユーリはバシッと決めるのが好きだろ? 『細かくて、たくさんくしゃくしゃ』みたいに言っても伝わらない」
ユーリ「じゃ、何て言えばいーの?」
僕「《周波数(しゅうはすう)が高い》と言えばいい」
ユーリ「しゅーはすー……」
僕「そう、周波数。(A)と(B)を見比べると、(B)の方が周波数が高いことがわかる。だから、(B)の方が音が高い」
ユーリ「……」
僕「そして、(A)と(C)を見比べると、(C)の方が周波数が低いことがわかる。だから、(C)の方が音が低い。 このグラフを、周波数が高い順に並べると、(B)>(A)>(C)という順番になる。この順番はそのまま音が高い順になる。 だから、最も音が高いのは(B)で、最も音が低いのは(C)になる」
ユーリ「ちょっと待ってよ、お兄ちゃん。その《周波数》ってどーゆー意味?」
僕「いいぞ、いいぞ! それは『周波数の定義』を聞いてるんだね。それは正しい態度!」
ユーリ「だって、意味わかんなかったら意味ないじゃん」
僕「まさにそうだよね。意味分からない言葉に言い換えても意味はない。その通り。 周波数は『一定の時間で何回振動したかを表した量』だよ。 たぶん、《音は波》のコーナーなんだから、どこかに定義を掲げたパネルがあると思うんだけど……」
ユーリ「パネル、パネル……あっ、あれ?!」
ユーリは、少し離れたところにあるパネルに駆け寄る。僕はユーリを追いかける。
振動数(周波数)
単位時間あたりの波の個数を振動数(しんどうすう)あるいは周波数(しゅうはすう)といいます。
$1$ 秒間あたりの波の個数はHz(ヘルツ)という単位で表します。
人間の可聴域は約 $20$ Hzから約 $20000$ Hzまでの範囲に収まっていますが、非常に個人差があります。
僕「このパネルでは周波数を『単位時間あたりの波の個数』と表現しているね」
ユーリ「お兄ちゃんはさっき何ていったっけ」
僕「『一定の時間で何回振動したかを表した量』」
ユーリ「単位時間ってなーに」
僕「ある決まった特定の時間のことだよ。ほら、パネルの下に例が出ている。『$1$ 秒間あたりの波の個数』はHzという単位で表すって書いてあるよね」
ユーリ「へるつ」
僕「うん、Hzでは $1$ 秒間を単位時間にしているわけだ。一定の時間を決めて、そのあいだに何回振動したかを数える」
ユーリ「単位時間のあいだに何回振動したか?」
僕「そうだね。《何回振動したか》というのは《波の個数が何個か》というのと同じ」
ユーリ「ふんふん」
僕「時間を決めずに、長い時間を掛けたとすると振動の回数は掛けた時間の分だけいくらでも多くなる。逆に短い時間しか掛けないなら、その間の振動の回数は少ない。 だから、一定の時間を決めてやらないと、振動の回数……つまり波の個数を比較しても意味がない」
ユーリ「そりゃそーだね」
僕「ここにはさらに例として、人間の可聴域が出てきてる。約 $20$ Hzから約 $20000$ Hzまでの範囲で……」
ユーリ「むむむ……ねえ、 $20000$ Hzってことは $1$ 秒間に $20000$ 個の波があるってこと?」
僕「そういうことになるね」
ユーリ「それすごくない? $20000$ 個だよ? $1$ 秒スタート……はいっ、ここまでで $20000$ 個の波! 想像つかなーい!」
僕「それが人間が耳で聴くことができる高い音の限界付近ということ。それだけの回数、鼓膜が振動する。それよりも高い音は聞こえない。それが超音波だね」
ユーリ「ちょーおんぱ! 超音波も音なの?」
僕「人間が聞こえないという特徴を除けば、超音波も音と同じだよ」
ユーリ「そーなんだ」
僕「あっちのコーナーには、高音を体験できるコーナーがあるね」
ユーリ「あっ、やりたいやりたい!」
高音体験コーナー
こちらの動画では、 $440$ Hzから $28160$ Hzまでの音が $7$ 段階で順に再生されます。
注意:大きな音が出ます。耳を痛めないようにボリュームを落としてください。
(音量注意)440Hzから28160Hzまでの正弦波 - YouTube
※免責:この動画は、低い音と高い音の違いを感じたり、普段は気に留めない非常に高い周波数の音を試しに聞いてみる、という意味で作ったものです。周波数の正確さも作者は保証しません。使用する機器によっても再生状況は異なります。すべてが音として聞こえる人はほとんどいません。高い音が聞こえないからといって、気に病んだり医学的な判断を行ったりしないようご注意ください。
僕「$20000$ 個の波じゃないけど、 $440$ 個の波の図がこっちのパネルにあるよ」
$440$ Hzの波($1$ 秒間)

ユーリ「これ、何? これ、波?」
僕「横軸が時刻で、このグラフの範囲がちょうど $1$ 秒間で、 $440$ Hzということは、 $440$ 個の波があるんだろうね。目で見て数えるのは難しそうだけど。 あ、こっちには $0.5$ 秒間のグラフがある」
$440$ Hzの波($0.5$ 秒間)

ユーリ「たいして変わんないじゃん!」
僕「いやいや、さっきよりも波には見えるね。個数はやっぱり数えられないけど」
ユーリ「えーと、 $440$ Hzは $1$ 秒間に $440$ 個の波だから……てことは、 $0.5$ 秒だと $220$ 個あるの?」
僕「計算ではそうなるね。周波数は《単位時間あたりの波の数》だから、周波数に時間を掛ければ波の個数になる」
$$ 440 \times 0.5 = 220 $$ユーリ「$220$ 個……」
僕「ねえユーリ、こっちには $0.1$ 秒間のグラフがあるよ。同じ周波数、 $440$ Hzの音だ」
$440$ Hzの波($0.1$ 秒間)

ユーリ「うーん、周波数 $440$ Hzの音が $0.1$ 秒だと、 $44$ 個の波があるってことかあ……」
$$ 440 \times 0.1 = 44 $$僕「そうなる」
ユーリ「はっきり言って、音って《すごい》ね。 $440$ Hzは、 $1$ 秒間に $440$ 個! ハンパなく《すごい》個数だよね。 んにゃ……なんで $440$ なんて中途半端な数なんだろ」
僕「$440$ Hzはオーケストラの音合わせをする周波数じゃなかったかな。《ラ》の音」
ユーリ「あーおもしろかった。じゃっ、次のクイズパネルに行こー!」
僕「もう順路がぐちゃぐちゃになったなあ……《次》ってどこだろう」
ユーリ「あれじゃない?」
クイズ(音が聞こえる条件)
真空中で音を鳴らしても、音は聞こえません。 それはどうしてですか。
僕「なるほどね。これも簡単なクイズだね」
ユーリ「これは、空気がないからでしょ?」
僕「まあ、そうだね。真空中には空気がない。だから音は聞こえない」
ユーリ「おっけー。スタンプ押して、次のパネル!」
僕「ところで、空気がないとどうして音が聞こえないんだろう」
ユーリ「おっと、また来たお兄ちゃんの《どうして》攻撃」
僕「攻撃じゃないよ。さっきのクイズパネルと同じ。《どうして》を考えないとつまらないよね」
ユーリ「だって、空気がないと音が聞こえないじゃん? ……えーと、これは理由としてはおかしーね」
僕「おかしいね。空気がないと音は聞こえない。なぜならば、空気がないと音が聞こえないから……これは理由になってないなあ」
ユーリ「でも、他に説明しようがなくね?」
僕「そんなことないよ。真空だと空気のように《振動を伝えるもの》がない。だから音が伝わらない。ほら、こっちの解答パネル」
クイズの解答(音が聞こえる条件)
音は波です。
真空中には音の波を伝えるものがありません。
ですから、真空中で音を鳴らしても、音は聞こえないのです。
ユーリ「……」
僕「僕は《振動を伝えるもの》と言ったけど、このパネルでは《音の波を伝えるもの》と表現しているね」
ユーリ「音の波を伝えるものがないから聞こえない……ねー、これだとユーリの『空気がないから聞こえない』でもよくね?」
僕「たとえ《空気》がない場合でも、《音の波を伝えるもの》があったら聞こえるからねえ。 たとえば、プールの水にもぐって、石か何か固いものをコツコツ叩いたら、離れていても聞こえるよね。 空気がなくても、水が音の波を伝えるから音は聞こえる」
ユーリ「プールの中って真空じゃないじゃん!」
僕「そうだけど、言いたかったのは《空気がないから音が聞こえない》と説明してしまうと、大事なポイントを外しちゃうってこと。 《空気という特定のもの》がないんじゃなくて、《音の波を伝えるもの》が何もないという点が大事なんだ」
ユーリ「むー」
僕「ええと、媒質の説明はどこだろう……あっちにある」
ユーリ「待ってよ!」
媒質
一般に、波を伝えるものを波の媒質(ばいしつ)といいます。
たとえば、空気や水は音の波を伝える代表的な媒質です。
僕「このパネルでは媒質という言葉を説明しているね」
ユーリ「ばいしつ」
僕「空気や水は音の波を伝える。それ以外でも、たとえば木とか金属も音の波を伝えるね」
ユーリ「あ、階段の手すり!」
僕「手すり?」
ユーリ「ほら、金属の手すりがある長い階段あるじゃん。手すりをコンコン叩くとワンワン響く。あれも音の波?」
僕「ああ、そうだね。そういうふうに音の振動……音の波を伝えるものは音の波の媒質だよ」
ユーリ「待って。音を聞くとき、最後の最後は空気が必要だよね。だって、音を聞くのは耳だから、耳の中の空気が振動しなくちゃ」
僕「確かに。でも、骨伝導(こつでんどう)ヘッドフォンってあるよね。頭蓋骨のような身体の骨を使って音を伝えるんだ」
ユーリ「そっか。骨が媒質ってこと?」
僕「そういうこと! 骨を媒質にして音を伝えている。知った言葉をすぐ使ってみるの、いいね!」
ユーリ「へへー、もっとほめて」
僕「まあ、このくらいで」
ユーリ「ちぇっ」
僕「ところで《波の定義》はどこだろう。順路を考えずに見てきたからなあ……」
ユーリ「波の定義?」
僕「そう。《音は波》のコーナーだから、どこかに《波の定義》パネルがあると思うんだけど……人が多くてわからないね。あれかな?」
波
一般に、振動が伝搬する現象を波(なみ)といいます。
ユーリ「……ねえお兄ちゃん。ユーリ、お兄ちゃんから教えてもらったことあるよね、これ」
僕「そうだっけ」
ユーリ「うん。波動の話、お兄ちゃんから聞いたもん。そのときもこんな感じの定義だった」
僕「そりゃそうだ。振動が伝わっていく現象が波。振動が耳に伝わってきたとき音が聞こえると感じる。音は波なんだね。 だから《波のことを研究する》のは、《音のことを研究する》ことにもつながっていく」
ユーリ「真空中には音を伝える媒質がないから、音が伝わらない」
僕「そうそう。ところで、さっきからパネルに何回も『一般に』と書かれていたよね」
ユーリ「いっぱんに? そーだっけ」
僕「そうだよ。たとえば、こんなふうに」
ユーリ「二回だけ」
僕「どうして、『一般に』と書かれているかわかる?」
ユーリ「わかんにゃい」
僕「それは、いま話しているよりも一般的なことをいいたいからだね」
ユーリ「そりゃそーだ」
僕「『一般に』という言い方は、何か言葉を説明するときによく出てくる。 わかりやすい具体的なものについて、それがどんなものかを説明して、相手がよくわかったなと思ったら、 そこで『一般に、○○のことをナントカという』みたいに使うんだね」
ユーリ「へー……そんなの、考えたこともなかったよ。説明のときに使う言葉なんて」
僕「『一般に』というのは 『いままでは具体的な話をしたけれど、それはあくまで具体例に過ぎなくて、そういう種類のことを総称していうと』 という意味で使う」
ユーリ「そーしょーして?」
僕「『総称して』は『いろんなものをまとめて』という意味」
ユーリ「それで? 媒質とか波だと何がいろんなものなの?」
僕「うん。さっきのパネルで言うと、こんなふうに読み解ける」
ユーリ「うっわー! すごく理屈っぽい……けど、こーゆーの、嫌いじゃないぜっ!」
僕「だから、説明の中で『一般に』という言い方が出てきたときは、 話がスッと広がっていることに注意する必要がある。 そこまでの具体的説明をもとにして、広がった世界のことをイメージする必要があるんだね。 でないと『一般に』という言い方が出てきた真意をつかみそこねるから」
ユーリ「そーいえば、お兄ちゃんって『一般化』するの大好きだよねー!」
僕「そうかな」
ユーリ「《一般化大好き高校生》だ!」
僕「謎概念を作るなって」
この記事は期間限定で「ただいま無料」となっています。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(第281回終わり)
(2020年1月24日)