第265回 シーズン27 エピソード5

分数を極める：表記と評価（前編）

図書室にて

テトラ「……確かに黄金比 $\phi$ と同じ結果になりました」

僕「この、 $$ x = 1 + \frac{1}{x} $$ という式自体は、テトラちゃんの発見を連分数全体に適用したと考えることもできる」

テトラ「ああ……」

僕「無限に続くから、《左辺全体》は《右辺の分母》と同じ形になっているんだね」

テトラ「なるほどです」

僕「うん、だからこれでテトラちゃんの不満に答えたことになるよね」

テトラ「ふ、不満？」

僕「この連分数が黄金比を表すということを、自分で計算したいよう、計算したいよう！　って言ってたから（第264回参照）」

テトラ「ああ……でも、それは不満じゃないですよう。不満という表現に不満ですっ！」

僕「ごめんごめん」

テトラ「それにしても、方程式が突然出てくるのにはびっくりしました。 いえ、当たり前のことなんですけれど」

僕「そうだね。 $$ x = 1 + \frac{1}{x} $$ という等式を満たす $x$ を求めることになるからだね。この場合は二次方程式を解くことになる」

テトラ「そうなんですが……」

僕「ん？」

テトラ「……あたしの中で、方程式がくるりと逆転したような感覚があります」

僕「方程式が逆転するって、どういう意味だろう」

テトラ「あのですね、『この方程式を解け』という問題ってよく出てくるじゃないですか」

僕「数学の試験なんかで？」

テトラ「そうです。そのときは、方程式を解くことが問題になります。 つまり……たとえていうなら、方程式という敵がやってくるので、 その敵に立ち向かってやっつけるんです」

僕「うん、わかるよ」

テトラ「でも、いま連分数が黄金比を表していることを調べたときには、 方程式は敵じゃありませんでした。 自分の武器というか、自分のバトルの援軍というか……あたしのイメージ、伝わってます？」

僕「何となくは」

テトラ「あたしは……あたしたちは、連分数の値を調べようとしていて、 その形に注目して、連分数の値が満たす等式を見つけましたよね。 そこまでは、よくわからないまま探っている感覚でした。 でもそこからは《あとはこの方程式を解けばいい》という感覚に変わったんです」

僕「うんうん」

テトラ「もっとも、先輩に言われるまで《あとはこの方程式を解けばいい》ということにあたしは気付かなかったんですが……で、でも、 『これはただの二次方程式なんだから、あたしにも解ける！』とわかったときには、すごくうれしくなりました。 それは、まるで、バトル中に援軍が到着したようなイメージなんです。立ち向かう敵じゃなくて、自分の側に来てくれた援軍です。仲間です」

僕「なるほどね。方程式は敵じゃなくて、味方なんだ。それが逆転したような感覚ということ？」

テトラ「ですです」

僕「そういえばテトラちゃんはよく、数学的概念のことを《武器》にたとえるよね。 武器を増やすとか、新しい武器を手に入れるとか」

テトラ「あっ、えっと……お、《お友達》にたとえることもありますよ……」

僕「ということは、《お友達》は《武器》なんだ！」

テトラ「や、やめてくださいっ、もうっ……」

僕「ごめんごめん……で、連分数はテトラちゃんの《武器》になったの？」

テトラ「いえ……まだ《お友達》にはなっていませんね。そもそも、連分数って何なんでしょうか？」

僕「連分数とは何か。これまでに僕たちが扱ってきたようなものだよね」

テトラ「はい。連分数が数である、ということはわかるんですけれど……」

僕「うーん、そこは、ちょっと注意が必要なところかもしれないよ」

テトラ「え？」

僕「連分数は数そのものじゃなくて、数の表記だからね」

テトラ「数じゃなくて、数の表記……」

僕「うん。これはユーリにも話したことがあるんだけど、 《数そのもの》と《数の表記》は注意深く区別した方がいいんだ」

ユーリ「はいっ、ここで宣伝タイムです。 お兄ちゃんとかわいいユーリとの楽しい数学トークは 『数学ガールの秘密ノート／ビットとバイナリー』 でお読みくださーい！　《数そのもの》と《数の表記》についても出てきまーす！」

僕「なんだいまの」

テトラ「数の表記というのは、数をどのように書き表すかという意味ですよね？」

僕「そうだね。連分数じゃなくても、ふつうの分数について考えてみてもわかるよ。たとえば分数表記で、 $$ \frac12 $$ と書いたものと、小数表記で、 $$ 0.5 $$ と書いたものがあったとする。 $\frac12$ と $0.5$ は表記としては異なるけれど、値としては等しいよね」

テトラ「ははあ……わかりましたよ。先輩のおっしゃる意味がよくわかりました。 確かに、分数というのは数そのものではないですね。数を書き表している言葉というか、書き方というか」

僕「うん、それが表記」

テトラ「そうですね。 $\frac12$ のような分数は数の表記。 $0.5$ という小数も数の表記」

僕「そうなんだよ。僕たちは当然のように、 $$ \frac12 = 0.5 $$ と書くけど、等号（$=$）は左辺と右辺の値を比較しているんだね。表記を比較しているわけじゃない。 もしも表記を比較したら $\frac12$ と $0.5$ は異なるものになっちゃう」

テトラ「《表記と値》というのは、まるで《言葉と意味》の関係のようですね。 見えない値を見えるようにするのが表記で、伝わらない意味を伝えるようにするのが言葉」

僕「なるほどね」

テトラ「思い出してきました……以前、既約分数のことを話していたときに、 先輩が表記法の話をしてくださいましたね。つまり、約分することの意味です（第177回参照）」

僕「そうだったっけ」

テトラ「そうです。 $\SQRT2$ が有理数でないことの証明で……あらら？　先輩、あたし、 新しい問題を見つけてしまいました」

僕「発見、はっけん？」

テトラ「はい。先ほど黄金比 $\phi$ を連分数で表しましたよね」

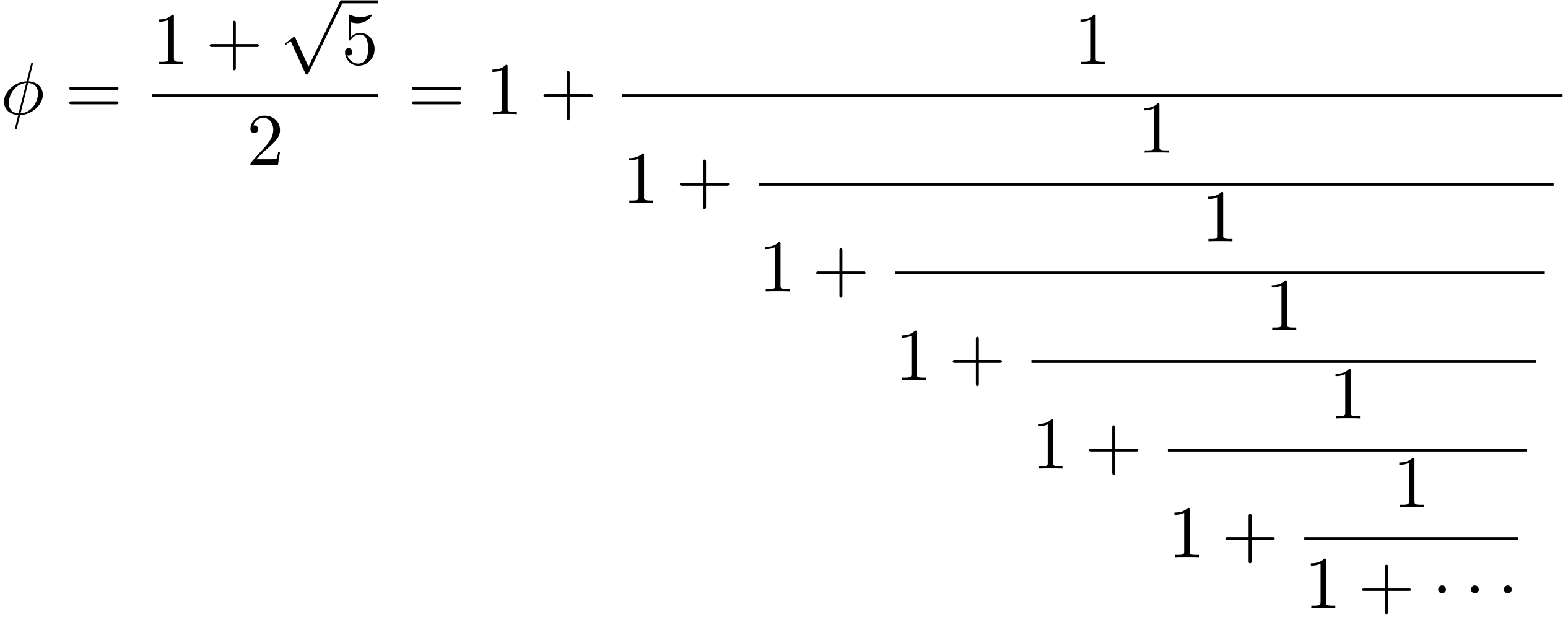
僕「そうだね。連分数で黄金比を表記したわけだ」

テトラ「同じように考えれば、《$\SQRT2$ を連分数で表す》こともできるんじゃないでしょうか！」

僕「なるほど……うん、できるね。まず」

テトラ「ストップです！　あたし考えますから、先輩は何も言わないでくださいね！　ヒントもダメですっ！」

僕「……」

テトラ「……たっ、たぶん、できましたっ！」

僕「$\SQRT2$ を連分数で……」

テトラ「はいっ、表せました。お聞き下さい。 まずあたしは《与えられているものは何か》を考えました」

僕「おおっ、いきなりポリアの《問いかけ》だね」

テトラ「はい。《与えられているもの》は、 $\SQRT2$ で表される値です。そして《求めるものは何か》というと、 $\SQRT2$ の連分数表記です。ですよね」