![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。 好奇心旺盛で根気強い《元気少女》。言葉が大好き。
ミルカさん:数学が好きな高校生。 僕のクラスメート。長い黒髪の《饒舌才媛》。
ミルカ「テトラの《カード》は?」
テトラ「あっ、はい。これです」
テトラちゃんは村木先生からもらったカードをミルカさんに見せる。
テトラちゃんの《カード》
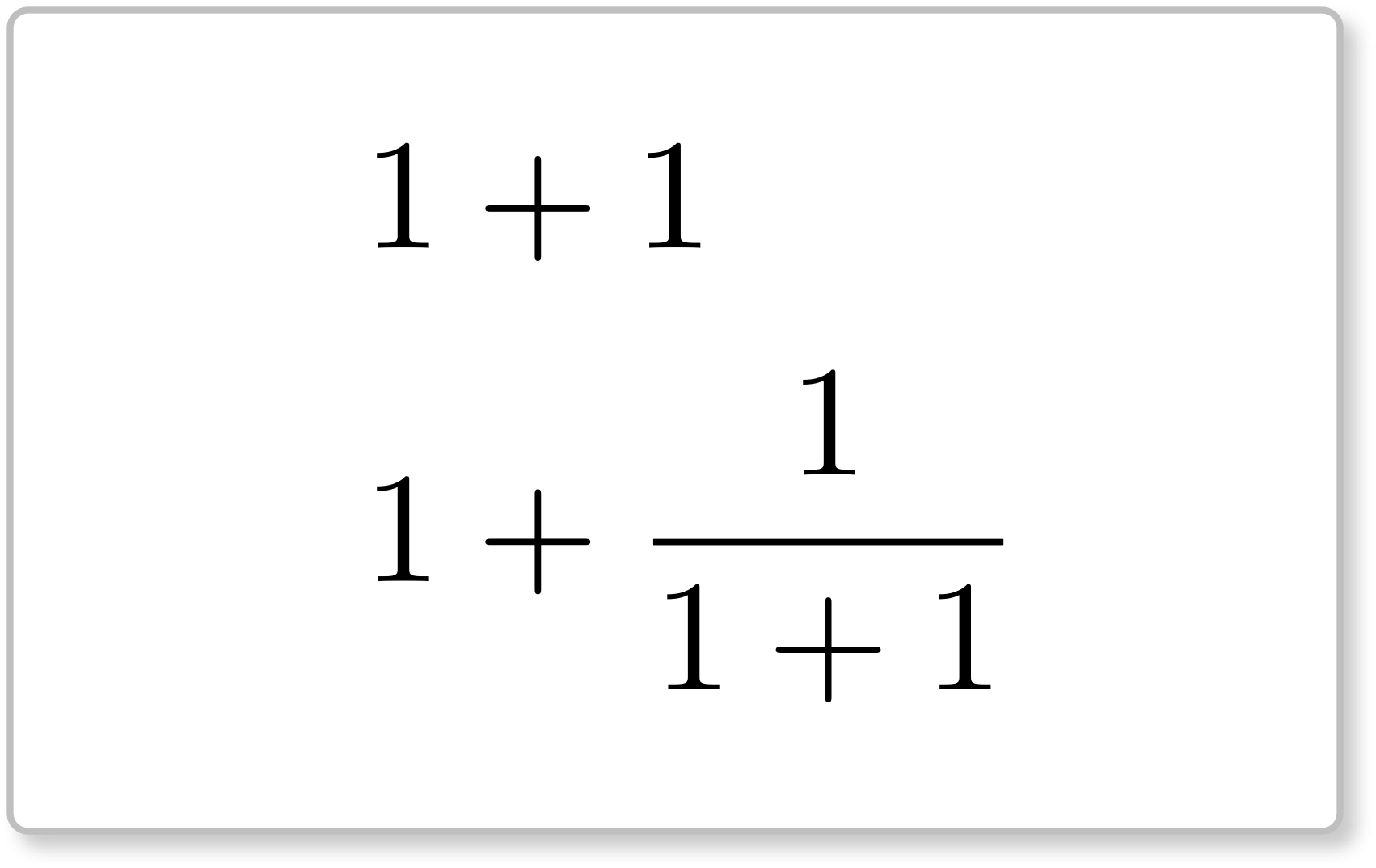
テトラ「調和数の収束について考えていたんです。この《カード》から出発して(第261回参照)」
僕「そうだね。逆数和とオレームの証明について、数列の収束を考えていたんだよ。 テトラちゃんの《カード》から、 $$ H_n = \frac11 + \frac12 + \frac13 + \cdots + \frac1n $$ と話を展開したんだ」
考えてみれば、ここから話が始まったんだなあ。
ミルカ「ふうん……では、私がもらってきた《カード》からは、何を展開する?」
ミルカさんはそう言って、新しい《カード》を僕とテトラちゃんの前に置いた。
ミルカさんの《カード》
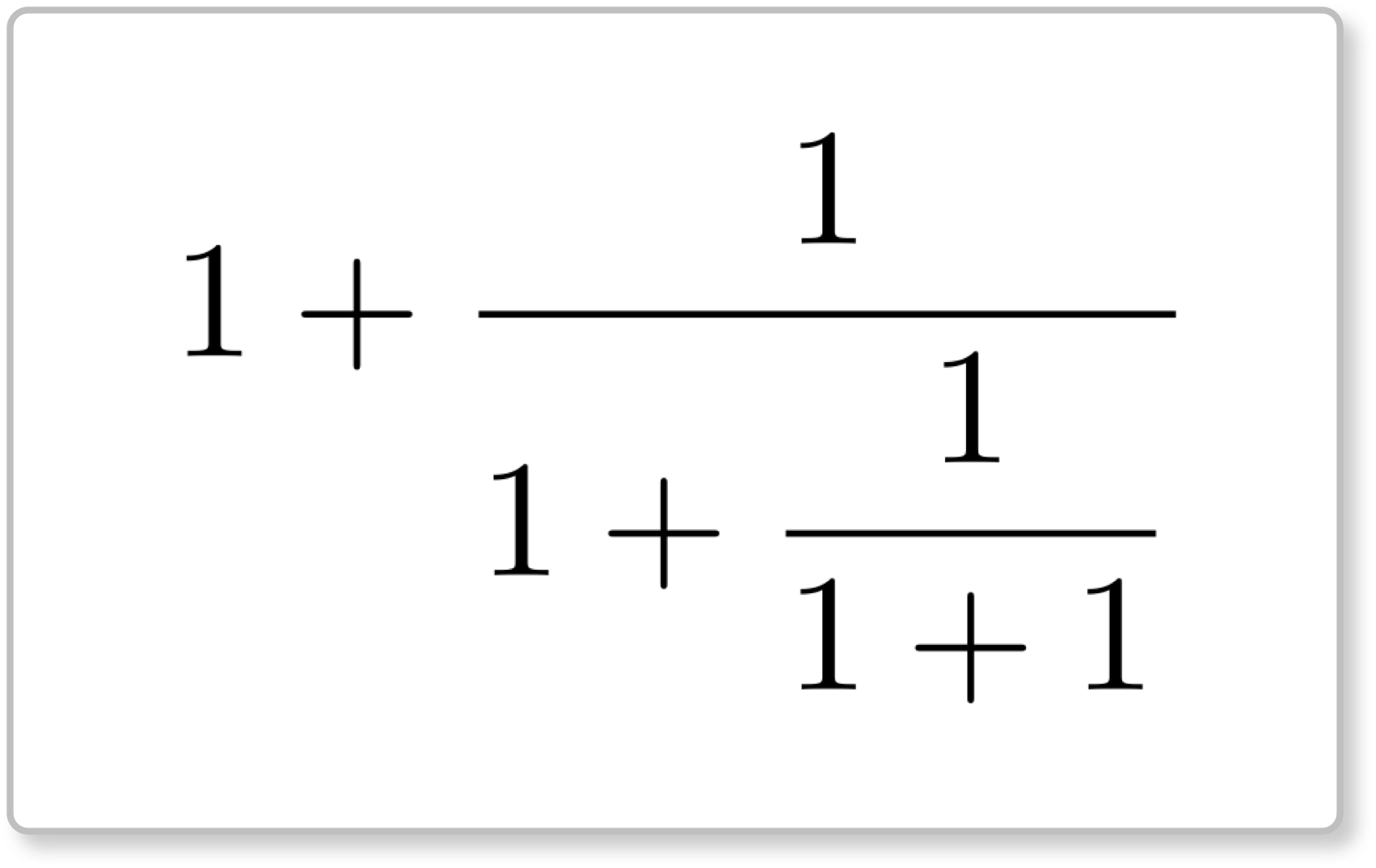
テトラ「$1+1$ がいっぱいですっ! これは、あたしの《カード》と同じ……じゃないですね。形は似ていますけど」
僕「なるほど! 連分数(れんぶんすう)の方向に進むのもおもしろいね!」
ミルカ「そう、連分数だ。この先を作りたくなる形をしている」
テトラ「連分数……分母に分数が入っていますね」
テトラちゃんはミルカさんの《カード》を前のめりになって見ている。
ミルカ「ふむ。私たちを深みに誘う形だ。こんな極限を考えたくなる」

テトラ「あっ! そういうふうに繰り返すんですかっ! あたしは分母の方に調和級数が入るのかと思いました」
僕「調和数 $H_n$ は $n \to \infty$ で正の無限大に発散するから、それを分母に入れた $1/H_n$ の極限は $0$ になっちゃうね」
ミルカ「連分数は楽しい。極限のために評価について考えたくなる」
僕「評価?」
ミルカ「そうだ。テトラの《カード》と私の《カード》を並べてみると、おもしろいことに気付く」
テトラちゃんの《カード》
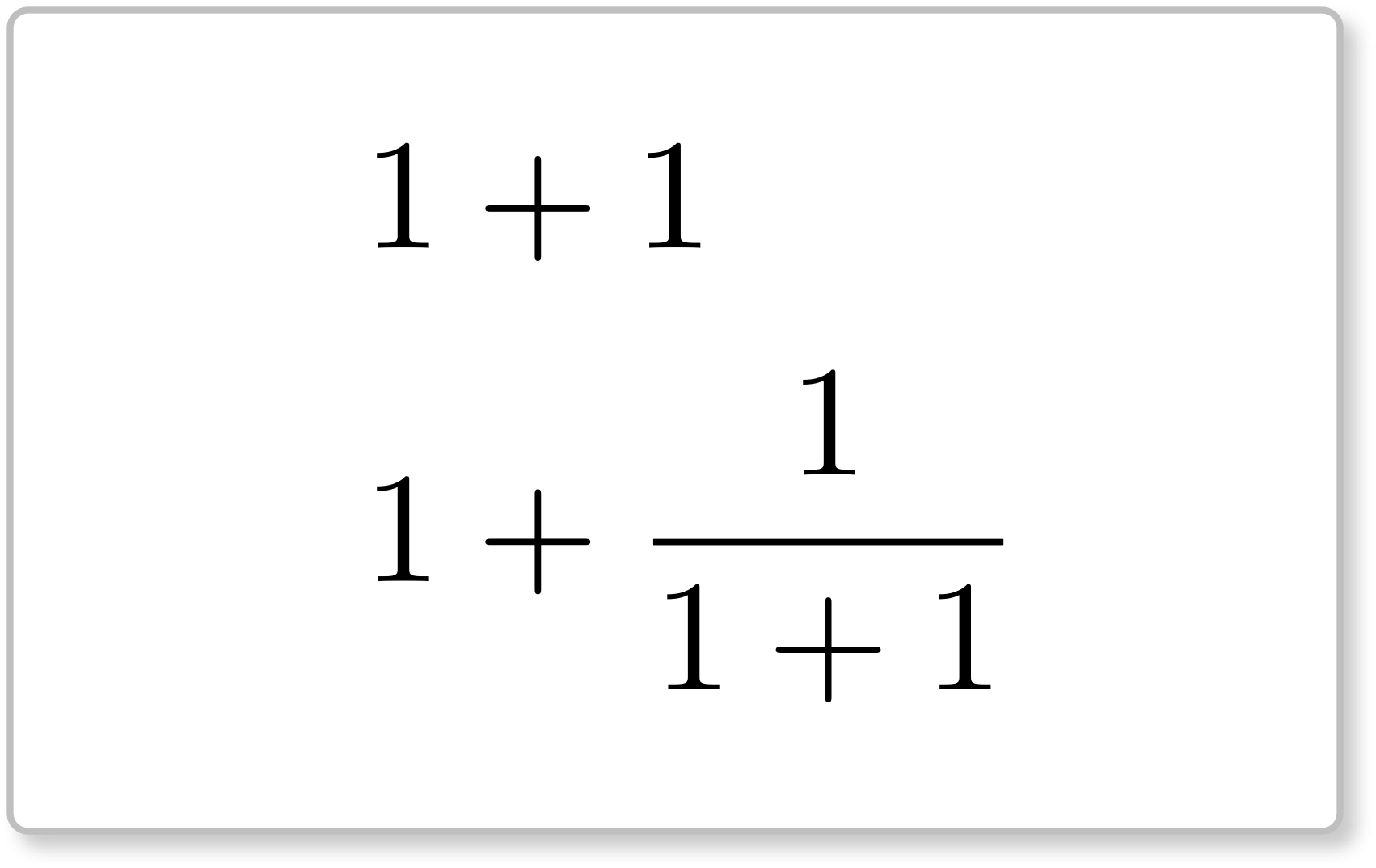
ミルカさんの《カード》

テトラ「おもしろいことというのは……?」
と、そのとき。
エィエィ「発見したで! 今日は連弾するんやろ?」
ミルカ「そうだった」
ピアノ少女のエィエィがミルカさんを連れ去ってしまった。
僕「……」
テトラ「……ミルカさん、行っちゃいました」
僕「エィエィとの約束があったのか」
テトラ「……あたし、連分数って初めて見ました。 こんな式を書いてもいいんですね。 分数の分母に分数の分母に分数の分母に分数の分母に分数の分母に分数……が入っているような式」

僕「そうだね」
テトラ「出てくるのは $1$ と $+$ と分数だけなのに、 式の書き方でずいぶん印象が違います。 でも、連分数っておもしろいんでしょうか」
僕「とは?」
テトラ「あ、いや、大げさといいますか……簡単なことを難しそうに見せる式、みたいな印象がちょっと……」
僕「ああ、そういう式はあるよね。 テレビのクイズ番組で $\sin$ や $\log$ や積分をこれ見よがしに出す式を見たことがある。 難しさを印象付けるために使う数式はちょっとねえ……でも、連分数はそれとは違う。ちゃんとおもしろさがあるんだ」
テトラ「この極限は、どんなふうに何を考えればいいんでしょう。分数の分母に分数の分母に分数の分母に……」
僕「うん。じゃあ、いっしょに考えてみようよ」
テトラ「はいっ!」
僕「極限を考えるときは、いきなり無限を考えちゃだめなんだ」
テトラ「ええっ?」
僕「無限を扱うのは難しいし、誤解を招くことが多い。いっぺんに考えようとするとまちがってしまう。 無限をいっぺんに扱えないからこそ、僕たちは極限という考え方を使うわけだし。 無限のことを考える前に、有限のことを考えるんだよ」
テトラ「有限のこと……?」
僕「調和級数のときもそうだったよね。 $H_{\infty}$ を考える前に $H_n$ のことを考えた。 $n$ という値に対して $H_n$ がどういう値なのかを考えることが大事だった」
テトラ「ああ……確かにそうですね。では、この連分数の場合は?」
僕「うん。こんなふうに $a_1,a_2,a_3$ という名前をつけてみよう」
$$ \begin{align*} a_1 &= 1+1 \\ a_2 &= 1+\frac{1}{1+1} \\ a_3 &= 1+\frac{1}{1+\frac{1}{1+1}} \\ \end{align*} $$テトラ「なるほどです。あたしの《カード》にあった式を $a_1$ と $a_2$ にして、ミルカさんの《カード》の式を $a_3$ にしたのですね」
僕「そしてこれは……」
テトラ「もちろん、計算できますっ! 無限や極限とはまったく関係ない、ただの分数計算ですから」
$$ \begin{align*} a_1 &= 1+1 \\ &= 2 \\ a_2 &= 1+\frac{1}{1+1} \\ &= 1+\frac{1}{2} \\ &= \frac{2+1}{2} \\ &= \frac{3}{2} \\ a_3 &= 1+\frac{1}{1+\frac{1}{1+1}} \\ &= 1+\frac{1}{1+\frac{1}{2}} \\ &= 1+\frac{1}{\frac{2+1}{2}} \\ &= 1+\frac{1}{\frac{3}{2}} \\ &= 1+\frac{2}{3} \\ &= \frac{3+2}{3} \\ &= \frac{5}{3} \\ \end{align*} $$僕「うん、具体的な計算は大事だよ……」
テトラ「まとめると、こうなります」
$$ \begin{align*} a_1 &= 2 \\ a_2 &= \frac{3}{2} \\ a_3 &= \frac{5}{3} \\ \end{align*} $$僕「……」
テトラ「同じように $a_4,a_5,a_6,\ldots$ を作ってみて、 その具体的な数を見て、第 $n$ 項となる $a_n$ を考える……ということですよね?」
僕「その通り。やっぱり $H_n$ を考えたときと同じだよね」
テトラ「確かにそうですね。一度に $H_{\infty}$ を考えるのではなく、まず部分和として $H_n$ を考えて、 その上で、 $n \to \infty$ の極限を考える……」
僕「そうなんだよ。そして、 $n \to \infty$ のとき、僕たちの数列 $a_n$ は……」
テトラ「待って! 教えないでください!」
テトラちゃんは、あわてて両手を振って僕を止める。
そうだよね。
謎は自分で解きたいよね。
この $a_1,a_2,a_3,\ldots$ はどんな数列なのか。
$n \to \infty$ で $a_n$ の極限はどうなるのか。

僕「わかった。何も言わないよ」
テトラちゃんは、 $a_4,a_5,a_6$ の計算を熱心に始めた。
テトラ「$a_4$ はこうです…… $$ \begin{align*} a_4 &= 1 + \frac{1}{ 1 + \frac{1}{ 1 + \frac{1}{ 1 + 1 }}} \\ \end{align*} $$ ……ですから、計算はすぐにできます。 $$ \begin{align*} a_4 &= 1 + \frac{1}{ 1 + \frac{1}{ 1 + \frac{1}{ 1 + 1 }}} \\ &= 1 + \frac{1}{ 1 + \frac{1}{ 1 + \frac{1}{ 2 }}} \\ &= 1 + \frac{1}{ 1 + \frac{1}{ \frac{3}{2} }} \\ &= 1 + \frac{1}{ \frac{5}{3} } \\ &= \frac{8}{5} \\ \end{align*} $$ ……あらら?」
僕「気付いた?」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2019年7月5日)