![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。 好奇心旺盛で根気強い《元気少女》。言葉が大好き。
問題($H_n$ の極限)
$n$ を正の整数($1,2,3,\ldots$)として、 $$ H_n = \frac11 + \frac12 + \frac13 + \cdots + \frac1n $$ と置く。 $n \to \infty$ のとき、 $H_n$ の極限は選択肢(1)と(2)のどちらになるか。
選択肢(1)$n \to \infty$ で $H_n \to \infty$ になる。(正の無限大に発散)
選択肢(2)$n \to \infty$ で $H_n \to H$ になる。ただし、 $H$ はある実数とする。(収束)
テトラちゃんと僕は、 $$ H_n = \frac11 + \frac12 + \frac13 + \cdots + \frac1n $$ で表される数を考え、$n \to \infty$のときの$H_n \to \REMTEXT{?}$について考えている。
いまは具体的な数をコンピュータで計算し終えたところ。
僕「$H_{10000} = 9.7876\cdots$ だね」
テトラ「$H_{10000}$ までいっても $10$ にすら届かないんですか……これは、収束するのが濃厚ですねっ!」
僕「そう思っちゃうよね。でも、そうじゃないんだ。 $n \to \infty$ のとき、 $H_n \to \infty$ になる。 つまり、 $H_n$ は正の無限大に発散するんだよ」
テトラ「えっ? ということは、選択肢(1)が正解なんですか?」
選択肢(1)$n \to \infty$ で $H_n \to \infty$ になる。(正の無限大に発散)
僕「そうだね」
テトラ「う、うーん……どうしてそんなことが言い切れるんでしょうか。 確かに、正の数を足していけばそれだけ大きくなるのはわかります。 でも、 $n$ がすごく大きくなると、 $\frac1n$ はすごく小さくなるはずです。 なのに、 $H_n$ がいくらでも大きくなれるなんて理解できません」
僕「うん。僕も初めてこれを知ったときはほんとうにびっくりしたし、納得できなかった」
テトラ「あっ、そうなんですね。先輩もびっくりなさった?」
僕「もちろんだよ。うまく理解できなかったし、納得できなかった」
テトラ「そういうものなんですね。ちょっと安心しました……でも、いまは納得していらっしゃるわけですよね」
僕「そうだね」
テトラ「こういう数学を納得できる感覚というのは、数学のセンスなんでしょうか。 あたしにはパッと理解できないんですが……」
僕「いやいや、数学のセンスとかそういうものじゃないよ。 《$H_n$ は正の無限大に発散する》とだけ言われて理解できるわけじゃないし、納得もできない。 僕が納得したのは、本に書いてあった証明を読んで、よく考えたからだよ」
テトラ「証明……?」
僕「うん、オレームの証明だね。 証明しないで『これはすごく大きくなる』とか『それほどは大きくない』のように考えても、 ものごとはハッキリしないよね。 そういうところ、ぼんやりと考えたくなるところをどうやって精密に考えるか……そこが大事なんだよ。 パッと理解するのが数学のセンスじゃあないんだ」
テトラ「なるほど……」
僕「じゃあ、 $H_n \to \infty$ になることを順序立てて説明しようか」
テトラ「はい、お願いします」
僕「僕たちがいま考えている $H_n$ というのは、 $\frac11 + \frac12 + \cdots + \frac1n$ という数だね。 $n$ という文字が入っているけど、大丈夫だよね」
$$ H_n = \frac11 + \frac12 + \cdots + \frac1n $$
テトラ「はい。 $n$ は $1,2,3,\ldots$ という正の整数です。一般的に考えたいので、 $n$ という文字を使っています。大丈夫です」
僕「そうだね。それで、僕たちは $n$ を決めたときに $H_n$ がどんな大きさを持っているのかを考えたいわけだ」
テトラ「そうですね。 $n \to \infty$ のときに $H_n$ がどうなるかを知りたいのですから」
僕「そういうこと。そこで、 $H_n$ を構成している $\frac11, \frac12, \ldots, \frac1n$ のひとつひとつに注目する」
テトラ「はい……」
僕「たとえば、これが成り立つ」
$$ \frac11 \LEQ \frac11 $$テトラ「はい? ……はい、そうですね。 $\frac11 = \frac11$ ですから、 $\frac11 \LEQ \frac11$ といっても構いません。 $1$ は $1$ 以下です」
僕「同じように、こんな式も成り立つ。当たり前のことを言ってるんだよ」
$$ \frac12 \LEQ \frac12 $$テトラ「はい、当たり前です」
僕「これはどうかな」
$$ \frac14 \LEQ \frac13 $$テトラ「これも、当たり前ですね。 $\frac14 < \frac13$ ですから、 $\frac14 \LEQ \frac13$ といっても構いません」
僕「そして、これもわかる」
$$ \frac14 \LEQ \frac14 $$テトラ「はい……あの、先輩、これが?」
僕「うん、ここまでは分数を一つ一つ比べてきたけど、最後の二つをこんなふうに足し算しても不等式が成り立つのはわかるよね」
$$ \frac14 + \frac14 \LEQ \frac13 + \frac14 $$テトラ「ええと、はい、わかります。 $\frac14 \LEQ \frac13$ という不等式と $\frac14 \LEQ \frac14$ という不等式で、 《小さいもの同士》を足して《大きいもの同士》を足して、その二つを比べています。 もちろん、《大きいもの同士》を足した方が大きくなります」
僕「そういうこと。厳密に言えば《小さい・大きい》は《以下・以上》だけどね……それで、と。 いまは $2$ 個の足し算をしたけど、次は $4$ 個の足し算をしてみよう。この不等式が成り立つことはわかる?」
$$ \frac18 + \frac18 + \frac18 + \frac18 \LEQ \frac15 + \frac16 + \frac17 + \frac18 $$テトラ「分母が $8,8,8,8$ と $5,6,7,8$ ですね……ははあ、なるほどです。 わかってきましたよ! この不等式は成り立ちますね。 左辺も右辺も $4$ 個の分数を足していますけれど、 $$ \begin{align*} \frac18 &\LEQ \frac15 \\ \frac18 &\LEQ \frac16 \\ \frac18 &\LEQ \frac17 \\ \frac18 &\LEQ \frac18 \\ \end{align*} $$ という $4$ 個の不等式を考えて、左辺同士、右辺同士を足したわけですね!」
僕「その通り! テトラちゃんはちゃんと式の形とその繰り返しを見抜いたね。 同じことをもう一回やってみよう。つまり、こう」
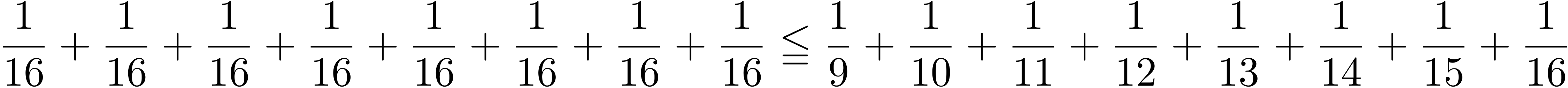
テトラ「あっ!」
僕「えっ!」
テトラ「$6$ 個ではなくて $8$ 個の足し算なのですね……」
僕「うん、そうだね。ここまでいくつかの不等式を書いてきたけど、 これをもう一度並べてみよう」
成り立つことを確認してきた不等式
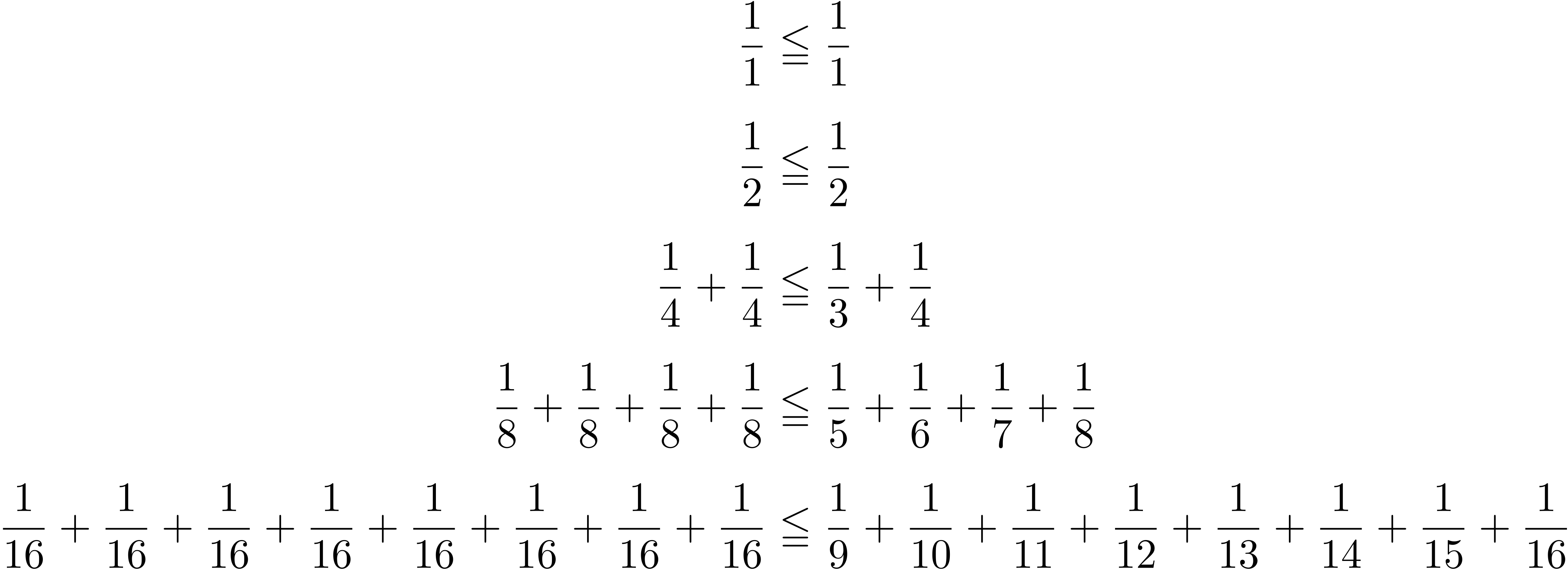
テトラ「なるほど……」
僕「左辺を計算すると、最初だけは $\frac11$ だけど、あとはぜんぶ $\frac12$ になることがわかる」
左辺を計算した不等式(成り立つ)
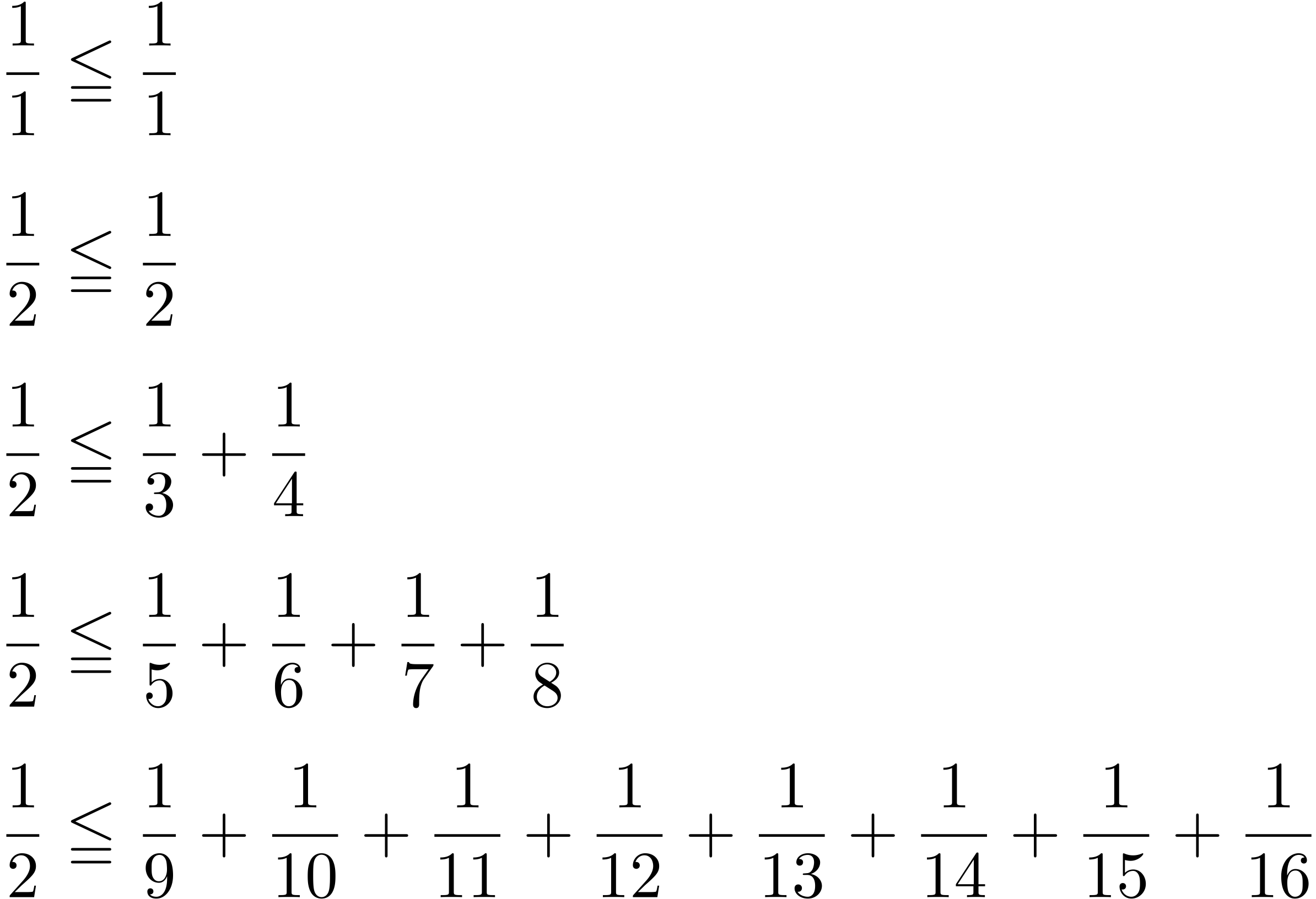
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2019年6月21日)