![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。 好奇心旺盛で根気強い《元気少女》。言葉が大好き。
僕「テトラちゃん、今日は何を考えているの?」
テトラ「あっ、先輩! 今日はですね、 $1+1$ を考えているんです!」
僕「え?」
ここは高校の図書室。いまは放課後。
テトラちゃんは僕の後輩。 いつも元気で、大きな目をぱちぱちさせながら数学に熱心に取り組む彼女。
でも、 $1+1$ を考えるって……いったいどういうことだろう。
テトラ「これですよ」
僕「ああ、村木先生の《カード》が来たんだね」
僕は、テトラちゃんが渡してくれた《カード》を見る。
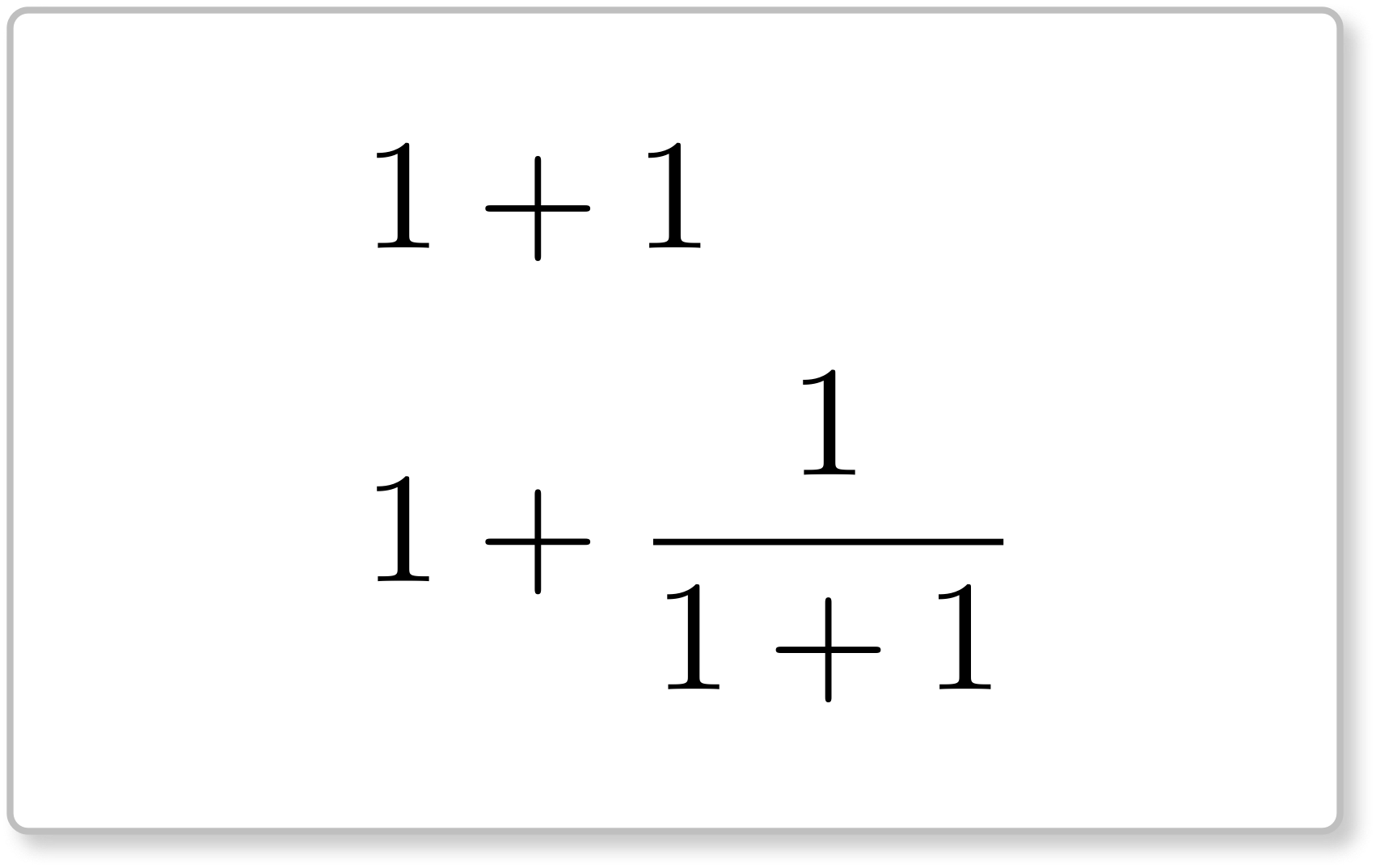
村木先生は、数学教師。
僕たちにときどき《カード》をくれる。
そこには数学の問題が書いてあったり、 数式がぽつんと一つ書かれていたり、 あるいは数学の定理が書かれていたり……
僕たちはそれをきっかけとして考える。 問題を解く。問題を作って解く。定理を証明する。証明できなかったら《例》を作る。 とにかく考えるんだ。
考えたからといって数学の成績に加点されるわけじゃない。 表彰されるわけでもない。僕たちはただ、楽しいから考えるのだ。
《カード》で明確に「これを考えよ」と示されるときもあるけれど、 単なる「思わせぶり」に見えるときもある。 でも、それはまあ、どうでもいいんだ。 僕たちは、《カード》をきっかけにして考えることを心から楽しんでいるのだから。
でも、今回のカードは……
テトラ「$1+1$ ですよね。思いっきり」
僕「思いっきり、 $1+1$ だね」
テトラ「もしかしてこれは、村木先生史上最大のシンプルな《カード》かもしれませんね、先輩っ!」
僕「確かに、これはシンプルだ……いや、違うよ、テトラちゃん」
テトラ「え?」
僕「ほら、いつだったか、何も書かれていない《カード》が来たことがあったよね」
テトラ「ああ……あの、丸いカード」
僕「そうそう(第139回参照)」
テトラ「それから、正五角形のカードもありましたね(第165回参照)」
僕「そういえば、そうだったね。ところで、テトラちゃんはこれで何を考えていたの?」
テトラ「はい。あたしはもちろん $1+1=2$ であることを知っています。 でも、それで終わりじゃおもしろくありませんよね。 それにこの《カード》には二つの式があります。つまり、 $$ 1+1 $$ と、 $$ 1+\frac{1}{1+1} $$ の二つです」
僕「そうだね」
テトラ「だから、あたしは《これをどんどん続けていったらどうなるか》を考えてみることにしました」
僕「これ?」
テトラ「はい。 $1+1$ は $1$ を使って $2$ を作っています。 続けていけば $3,4,5,\ldots$ と数が作れますよね」
$$ \begin{align*} 1+1 &= 2 \\ 1+1+1 &= 3 \\ 1+1+1+1 &= 4 \\ 1+1+1+1+1 &= 5 \\ &\vdots \\ \end{align*} $$僕「そうだね。 $1$ ずつ増える数列が作れる。 $2,3,4,5,\ldots$」
テトラ「それと同じことを $1+\frac{1}{1+1}$ でもできる、とあたしは思いました。 $\frac{1}{1+1}$ は $\frac12$ ですから、 こんなふうに書いていってみたんです」
$$ \begin{align*} 1+\frac1{1+1} &= 1+\frac12 = \frac32 \\ 1+\frac1{1+1+1} &= 1+\frac13 = \frac43 \\ 1+\frac1{1+1+1+1} &= 1+\frac14 = \frac54 \\ &\vdots \\ \end{align*} $$僕「今度は別の数列が作れたね。 $\frac32, \frac43, \frac54, \ldots$」
テトラ「はい、あたしはそれから、こんな数式も作ってみました…… $$ \begin{align*} & 1+\frac1{1+1} \\ & 1+\frac1{1+1}+\frac1{1+1+1} \\ & 1+\frac1{1+1}+\frac1{1+1+1}+\frac1{1+1+1+1} \\ & 1+\frac1{1+1}+\frac1{1+1+1}+\frac1{1+1+1+1}+\frac1{1+1+1+1+1} \\ & \vdots \\ \end{align*} $$ ……つまり、これは…… $$ \begin{align*} & 1+\frac12 \\ & 1+\frac12+\frac13 \\ & 1+\frac12+\frac13+\frac14 \\ & 1+\frac12+\frac13+\frac14+\frac15 \\ & \vdots \\ \end{align*} $$ ……ということです」
僕「なるほど、なるほど」
テトラ「ここまでは、何といいますか、《カード》をきっかけにして数式を書いただけなんですが…… $$ 1+\frac12+\frac13+\frac14+\frac15+\cdots $$ ……これを書きながら、あたしは少し変な感じがしました」
僕「変な感じ?」
テトラ「あの……笑わないでくださいね。当たり前のことなんですが、 $1$ をどんどん足して $1,2,3,4,5,\ldots$ と進むのはすごくキッチリしている感じがします。 キリがいいといいますか。 $3$ は $3$ ですし、 $5$ は $5$ です」
僕「うん……まあそうだね。僕も整数はどこか《きっちり》してる感じはするよ」
テトラ「はい、でも、それを分数の分母に持ってくると、そのとたん、そのキッチリ感はどこかに行ってしまいます」
僕「うーん、それはどういうことかなあ」
テトラ「えっとですね。さっき $1+\frac12+\frac13+\frac14+\frac15+\cdots$ と書いていて『あ、これ、足す数がだんだん小さくなっていく』 と思いました」
$$ \begin{align*} \frac12 &= 0.5 \\ \frac13 &= 0.333\cdots \\ \frac14 &= 0.25 \\ \frac15 &= 0.2 \\ \frac16 &= 0.1666\cdots \\ \frac17 &= 0.142857142857\cdots \\ &\vdots \\ \end{align*} $$僕「もちろん、それはそうだね。 $n$ が大きくなれば、 $\frac1n$ は小さくなる」
テトラ「はい。それはもちろんあたしもわかります。でも、何といいますか……もやもやと、えーっと、うまく説明できてませんね、あたし」
テトラちゃんは、両手をこねるような謎のジェスチャをしながら話すけど、意味はわからない。
僕「うーん、僕もテトラちゃんがどこにもやもやしているかわからないなあ。 《理解の最前線》を説明するのがすごくうまいテトラちゃんでも説明できないことがあるんだね」
テトラ「えっと、いえ、あたし、そんなに説明うまくないですっ! いつもどたばた考えているだけで……あ、 でも、先輩がいらっしゃるとうまく説明できるのかもしれません」
僕「僕が? 僕がテトラちゃんの説明に関係あるの?」
テトラ「はい……ありますね。 はい、確かにあります」
僕「へえ」
テトラ「あのですね。それはなぜかというと、 先輩はあたしの話にきちんと耳を傾けてくださるからです。 ですから、あたし、『ちゃんと説明しなくちゃ』と思えるんです。 それに、あいまいなところを指摘してくださったり、 あたしの勘違いをすっと正してくださったり……」
僕「なるほど。そういってくれるのはうれしいな」
テトラ「思い出しましたよ。あたし、家で数学の問題を解いているときも同じことをやってます」
僕「家で? 同じこと?」
テトラ「はい。問題を読んでいて行き詰まったときに、 先輩やミルカさんに向かって説明するつもりになるんです。 この問題はこういうことを尋ねているみたいですとか、条件はこれですとか、あたしは最初こんなふうに考えました……という具合に」
僕「ああ、それはおもしろいなあ!」
テトラ「それから、あたしは想像するんです。もしもここに先輩がいらしたら、なんて答えるだろう。 もしもここにミルカさんがいらしたら、どんなふうに言うだろう……それを想像します。 もちろん実際にはお二人はいらっしゃらないんですけど、想像することはできます」
僕「うん……」
テトラ「そうやって真剣に想像すると、不思議なことに解決のヒントが見つかることがよくあるんですよ!」
僕「なるほど……いまのテトラちゃんの話を聞いて思うんだけど、それは《ポリアの問いかけ》と似ているね」
テトラ「あっ、そうですね! 問いかけ上手なポリアさん」
僕「《定義にかえれ》や《求めるものはなにか》や《条件をすべて使ったか》や……それらは、 ポリアが僕たちに問いかけているともいえるし、 僕たちの中にポリアがいると想定して、 どんな問いかけをしてくるかを想像するのに似ている」
テトラ「確かにそうですね。 あの、でも、その問いかけは、数学じゃないですよね。 いえ、数学なんですけど、 いまあたしが見ている問題のことをポリアさんは知らないわけじゃないですか。 だってポリアさんのことを想像しているだけですから。 問題の具体的なことを何も知らないのに、ポリアさんの問いかけが考える助けになる。それってとっても不思議ですっ!」
僕「ほんとうにそうだね。不思議だ。きっと《考える》ことの大事な部分を支えてるんじゃないかなあ」
テトラ「《考える》ことの大事な部分……」
僕「ところで、さっきのこの式だけど、 テトラちゃんは《足す数がだんだん小さくなっていく》と言ってたよね」
$$ 1+\frac12+\frac13+\frac14+\frac15+\cdots $$テトラ「はい。そうですよね。分母がだんだん大きくなっていきますから」
僕「うん、足す数は $\frac12, \frac13, \frac14, \frac15, \ldots$ とだんだん小さくなっていく。 でも、いくら小さくても、それは $0$ よりは大きい数だよね」
テトラ「そうですね。たとえ $\frac1{100}$ まで行っても、 $\frac1{10000}$ まで行っても、 それは $0$ よりは大きいです。ちょっとだけ」
僕「だとしたら、 $$ 1+\frac12+\frac13+\frac14+\frac15+\cdots $$ はどうなると思う?」
テトラ「どうなるか?」
僕「つまり、極限を考えたとき、正の無限大に発散するか、 それとも、ある値に収束するか、どちらだろうか」
テトラ「あっ……極限を求めるんですね」
テトラちゃんの表情が固くなる。
僕「いやいや、そんなに警戒しなくてもいいよ。ちゃんとした問題にするね」
問題($H_n$ の極限)
$n$ を正の整数($1,2,3,\ldots$)として、 $$ H_n = \frac11 + \frac12 + \frac13 + \cdots + \frac1n $$ と置く。 $n \to \infty$ のとき、 $H_n$ の極限は選択肢(1)と(2)のどちらになるか。
選択肢(1)$n \to \infty$ で $H_n \to \infty$ になる。(正の無限大に発散)
選択肢(2)$n \to \infty$ で $H_n \to H$ になる。ただし、 $H$ はある実数とする。(収束)
テトラ「……」
僕「テトラちゃんは選択肢(1)と(2)がそれぞれ、何をいってるかはわかるよね?」
テトラ「は、はい。あたしの理解を聞いていただけますか」
僕「もちろん、どうぞ」
テトラ「まず選択肢(1)がいってるのは『$H_n$ はいくらでも大きくできる』ということですよね」
選択肢(1)$n \to \infty$ で $H_n \to \infty$ になる。(正の無限大に発散)
僕「うーん、気持ちはわかるけど、それはちょっと違うかな」
テトラ「ええっ! 『$H_n \to \infty$』というのは、『$H_n$ はいくらでも大きくできる』 という意味じゃないんですか?! あたし、いま、注意して『$H_n$ が無限大に等しくなる』と言わないようにしたんですが……」
僕「『$H_n$ はいくらでも大きくできる』という表現はあいまいだからね。たとえば、こんな(ア)と(イ)という二つの状況を考えてみようよ」
状況(ア)どんな $n$ を選んでも、 $H_{n} < H_{n+1}$ が成り立つ。
状況(イ)どんなに大きな実数 $H$ を選んでも、それに対してじゅうぶん大きな正の整数 $n$ を選べば、 $H < H_n$ にすることができる。
テトラ「……」
僕「(ア)と(イ)という状況は、どちらも『$H_n$ はいくらでも大きくできる』と表現できそうじゃない? でも状況(ア)と状況(イ)は違うよね」
テトラ「……確かにそうですね。テトラ、もう一度、選択肢(1)が表している状況を考えますっ!」
選択肢(1)$n \to \infty$ で $H_n \to \infty$ になる。
テトラちゃんはそう宣言して熟考モードに入った。
そうだよね。
納得するためには熟考が必要で、熟考するためには時間が必要だ。
僕「……」
テトラ「わかりました。選択肢(1)が表しているのは状況(ア)ではありません」
僕「そうだね」
テトラ「でも、あたしたちの $H_n$ は状況(ア)にあてはまりますよね?」
僕「うん、いいよ」
テトラ「あたしたちの考えてる $H_n$ というのは、 $$ H_n = \frac11 + \frac12 + \frac13 + \cdots + \frac1n $$ ですから、 $$ H_{n+1} = \frac11 + \frac12 + \frac13 + \cdots + \frac1n + \frac1{n+1} $$ です。しっぽに $\frac1{n+1}$ という正の数を足していますので、どんな $n$ に対しても、 $$ H_n < H_{n+1} $$ は成り立ちます。だって、 $$ H_n < H_n + \frac1{n+1} = H_{n+1} $$ ですから」
僕「うんうん、テトラちゃんは正しく理解しているよ」
テトラ「でも、この状況(ア)というのは《次の一歩》のことしか考えていません。 ほんのちょっとずつでも大きくなっていれば状況(ア)になりますから。 でも、選択肢(1)が表しているのは、そういう《次の一歩》だけを表しているんじゃありません。 極限は、そういう《次の一歩》だけの話じゃないんですっ!」
選択肢(1)$n \to \infty$ で $H_n \to \infty$ になる。
僕「いいよ、いいよ」
テトラ「選択肢(1)が表しているのは、状況(イ)の方ですねっ!」
状況(イ)どんなに大きな実数 $H$ を選んでも、それに対してじゅうぶん大きな正の整数 $n$ を選べば、 $H < H_n$ にすることができる。
僕「そう思っちゃうよね。でも、違うんだ」
テトラ「はい?」
僕「選択肢(1)が表しているのは、状況(ア)でもないし、状況(イ)でもないんだよ、テトラちゃん」
選択肢(1)$n \to \infty$ で $H_n \to \infty$ になる。
状況(ア)どんな $n$ を選んでも、 $H_{n} < H_{n+1}$ が成り立つ。
状況(イ)どんなに大きな実数 $H$ を選んでも、それに対してじゅうぶん大きな正の整数 $n$ を選べば、 $H < H_n$ にすることができる。
テトラ「状況(イ)でもない……あたし、やっぱり、極限だめですね。あたしには難しすぎます」
僕「そんなことないよ。テトラちゃんはさっきいいことを言ってたよ」
テトラ「あたし、何て言いましたっけ」
僕「『極限は、そういう《次の一歩》だけの話じゃない』ってね」
テトラ「選択肢(1)は状況(イ)を表しているものじゃない、というの、あたし、考えて、わかるでしょうか……?」
僕「うーん……どちらともいえない。気付くかもしれないし、気付かないかもしれない」
テトラ「だったら、考えますっ!」
テトラちゃんはそう宣言して再度、熟考モードに入った。
僕「……」
テトラ「先輩……?」
僕「ん?」
テトラ「これって結局、あたしは定義を確認していることになるんですね」
僕「そういうことになるね」
テトラ「だとしたら、あたしの勉強の仕方……理解のしかたが悪かったようです。 あたしは、選択肢(1)がどうしても状況(イ)を表しているもののように思えるからです。 テトラ、降参です」
選択肢(1)$n \to \infty$ で $H_n \to \infty$ になる。
状況(イ)どんなに大きな実数 $H$ を選んでも、それに対してじゅうぶん大きな正の整数 $n$ を選べば、 $H < H_n$ にすることができる。
僕「うん。選択肢(1)が表しているのは、次の状況(ウ)なんだよ。状況(イ)とそっくりだけど、違うよね」
状況(ウ)どんなに大きな実数 $H$ を選んでも、それに対してじゅうぶん大きな正の整数 $N$ を選べば、 $N$ より大きなすべての $n$ に対して、 $H < H_n$ にすることができる。
テトラ「え……あああああっ! そうでした、そうなんでした!」
僕「状況(イ)と状況(ウ)の違いはもう思い出したよね」
テトラ「はい……あたし、これは答えられたはずです。状況(イ)の方は、 $H$ に対して何か一個でも $H < H_n$ になるような $n$ を見つければいいんですね。 でも、状況(ウ)はまったく違います。 $H < H_n$ になるような $n$ を 一個 見つけるだけじゃだめで、 $N$ より大きな $n$ の すべてが $H < H_n$ になるような、そんな $N$ が見つからなくちゃだめ……そして、 $H_n \to \infty$ が表しているのは状況(ウ)の方です」
僕「そうだね。 $n \to \infty$ のとき $H_n \to \infty$ であるという主張は、 どんな $H$ に対しても、 $n = 1,2,3,\ldots,N$ という有限個の $n$ を捨ててしまえば、 残りの無限個の $n$ すべてについて $H < H_n$ になる、そんな $N$ が存在すると主張している」
テトラ「ううう……残念です。この話、先輩から何回か聞いていたはずです。 理解したと思っていたんですが……でも、もう大丈夫ですっ!」
僕「ところで、今度は選択肢(2)の方を確かめておくよ。 選択肢(2)はどういう状況を表しているかわかる?」
選択肢(2)$n \to \infty$ で $H_n \to H$ になる($H$ は実数)。
テトラ「はいはいはいっ!」
テトラちゃんは元気いっぱい挙手をした。いや、答えるのはテトラちゃんしかいないんだけどな。
僕「はい、テトラちゃん」
テトラ「もう、感覚を思い出しましたよ。 さきほどと同じように考えればもう大丈夫です。 さっきは $H_n \to \infty$ でしたから、 $H < H_n$ について考えましたけど、 今度は、 $H$ に近付いていけばいいんですね」
僕「そうだね。どんなに小さな正の数 $\EPSLN$ を選んでも……」
テトラ「あっ、やめてください。あたし、自分でいえます」
状況(エ)どんなに小さな正の数 $\EPSLN$ を選んでも、 それに対してじゅうぶん大きな正の整数 $N$ を選べば、 $N$ より大きなすべての $n$ に対して、……あらら?
僕「え?」
テトラ「《$H_n$ と $H$ が $\EPSLN$ 以上離れていない》」
僕「絶対値」
テトラ「そうですね。そうでした」
状況(エ)どんなに小さな正の数 $\EPSLN$ を選んでも、 それに対してじゅうぶん大きな正の整数 $N$ を選べば、 $N$ より大きなすべての $n$ に対して、 $\ABS{H - H_n} < \EPSLN$ にすることができる。
僕「はい、正解。これで選択肢(1)と(2)が何をいってるかよくわかった」
問題($H_n$ の極限)
$n$ を正の整数($1,2,3,\ldots$)として、 $$ H_n = \frac11 + \frac12 + \frac13 + \cdots + \frac1n $$ と置く。 $n \to \infty$ のとき、 $H_n$ の極限は選択肢(1)と(2)のどちらになるか。
選択肢(1)$n \to \infty$ で $H_n \to \infty$ になる。(正の無限大に発散)
選択肢(2)$n \to \infty$ で $H_n \to H$ になる。ただし、 $H$ はある実数とする。(収束)
テトラ「ようやく……これでようやく問題に取り組めるんですね。 でも、もうわかります。正解は選択肢(2)ですね!」
僕「いきなり答えが出てきたけど、テトラちゃんは、どうして選択肢(2)だと思ったんだろう」
テトラ「どうして選択肢(2)だと思ったか……ですか。 $n$ が大きくなると、 $H_n$ も大きくなります。 でも、その大きくなる度合いというのは次第に小さくなりますよね。 だって、 $\frac12, \frac13, \frac14, \ldots$ となって、やがて $\frac1{10000}$ にもなるわけですし」
僕「それはそうだね」
テトラ「大きくなる度合いが次第に小さくなっていくのに、 選択肢(1)のような状況は考えにくいです。 どんなに大きな $H$ を選んでも、ずっと大きくなるなんて…… だって、 $H = 10000$ でもいいわけですよね。 $H_n$ がそんなに大きくなるとは思えません」
僕「テトラちゃんは $H_n$ はある数 $H$ に収束すると予想したんだね。でも、そうかな?」
テトラ「先輩。引っかかりませんよ。 そうですよ。《例示は理解の試金石》なんですから、 実際に少し計算してみましょうっ! $10000$ は無理ですけど……」
僕を制止して、テトラちゃんは電卓を使って計算を始めた。
僕「どう?」
テトラ「う、うーん……計算して、余計にわからなくなってしまいました。 あたりまえですけれど、地道に増えていきますので、もしかしたらすごくゆっくりなペースだけど、 どんなに大きな $H$ を持ってきても、いつかはそれを越えることができるのかもしれません」
僕「確かに《例示は理解の試金石》は大事だけど、 それだけで発散するか、収束するかの判断は難しいね」
テトラ「せ、せめて $H_{10000}$ の具体的な値を求めてみたいです!」
僕「なるほど?」
$$ H_{10000} = \frac11 + \frac12 + \frac13 + \frac14 + \cdots + \frac1{10000} = \REMTEXT{?} $$
テトラ「あっ、わかりました。コンピュータさんの力を借りましょう!」
テトラちゃんは司書室に行き、 瑞谷先生にお願いしてコンピュータを使わせてもらうことに成功。
僕「プログラミングするの?」
テトラ「WolframAlphaを使うんです。先日リサちゃんに教えてもらったサイトですよ」
テトラちゃんは「$\texttt{1/1 + 1/2 + 1/3 + ... + 1/10000}$」とタイプして……答えが出た。
僕「$H_{10000} = 9.7876\cdots$ だね」
テトラ「$H_{10000}$ までいっても $10$ にすら届かないんですか……これは、収束するのが濃厚ですねっ!」
僕「そう思っちゃうよね。でも……」
この記事は期間限定で「ただいま無料」となっています。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(第261回終わり)
(2019年6月14日)