![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/確率の冒険』として書籍化されています。
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。 好奇心旺盛で根気強い《元気少女》。言葉が大好き。
問題(一般化した未完のゲーム)
$A$ と $B$ の二人がコイン投げのゲームをする。
コインを投げて $A$ の面が出たら $A$ の得点が $1$ 点増える。
コインを投げて $B$ の面が出たら $B$ の得点が $1$ 点増える。
最初は $A$ も $B$ も得点は $0$ 点である。
コインを何回か投げて、得点が先に《ある得点》に達した方が勝ちとなり、勝った方が賞金を総取りする。
ところが、ゲームを途中で中断しなければいけなくなり、賞金を $A$ と $B$ の二人で分配することになった。
中断した時点で、 $A$ が勝利するまでの残り得点は $a$ 点である。
また、中断した時点で、 $B$ が勝利するまでの残り得点は $b$ 点である。
中断せず継続したときに $A$ が勝利する確率 $p(a,b)$ を求めよ。
$a$ と $b$ はどちらも正の整数とする。
テトラ「これまでにわかったことは、こうですね」
$$ \begin{align*} p(1, 1) &= \frac12 \\ p(1, 2) &= \frac34 \\ p(2, 1) &= \frac14 \\ p(2, 1) &= 1 - p(1, 2) \end{align*} $$僕「そうだね。 $p(1, 1) = \frac12$ で気付いたけど、こういう式も成り立つよ」
$$ p(1, 1) = p(2, 2) = p(3, 3) = \cdots = \frac12 $$テトラ「なるほどです。 $A$ と $B$ の残り点数が等しいときには、 $A$ が勝つ確率は確かに $\frac12$ です。 ああ、これは同点だったらちょうど半分ずつにしたい気持ちにぴったりですね」
僕「これ、出てきたよね」
テトラ「出てきた?」
僕「さっき、テトラちゃんが $p(2, 1)$ を計算するときに出てきた。 $1$ 回目に $A$ が出たとすると《$A$ も $B$ も残り $1$ 点という状況》になったよね。その状況で $A$ が勝つ確率って、 $p(1,1)$ じゃない?」
テトラ「ああ、確かにそうです。あっ、これも関数 $p(x,y)$ の性質?」
僕「そうだね。僕たちが《小さな数で試す》ときに探しているものの一つ。これがいえる」
$$ p(2, 1) = \frac12p(1, 1) $$テトラ「……なるほどっ! 先輩、先輩! これ、図をなぞっているような式ですっ!」
僕「図をなぞっているというのは?」
テトラ「はい。いま先輩が書いた $p(2, 1) = \frac12p(1, 1)$ という式を読むとき、 あたしは図と対応させていきました。 まず、 左辺の $p(2, 1)$ を読むとき、 《$A$ が残り $2$ 点、 $B$ が残り $1$ 点という状況から、 $A$ が勝つ確率》 と考えました」
僕「そうだね。それは正しいよ」
テトラ「そして右辺の $\frac12p(1,1)$ を読むとき、 《$A$ が出る確率》である $\frac12$ と、 《$A$ も $B$ も残り $1$ 点という状況から、 $A$ が勝つ確率》 との掛け算になっている…と考えました。 そのときあたしは図をなぞりながら、式を読んでいったんです」
$p(2, 1)$ を考えるときの状況
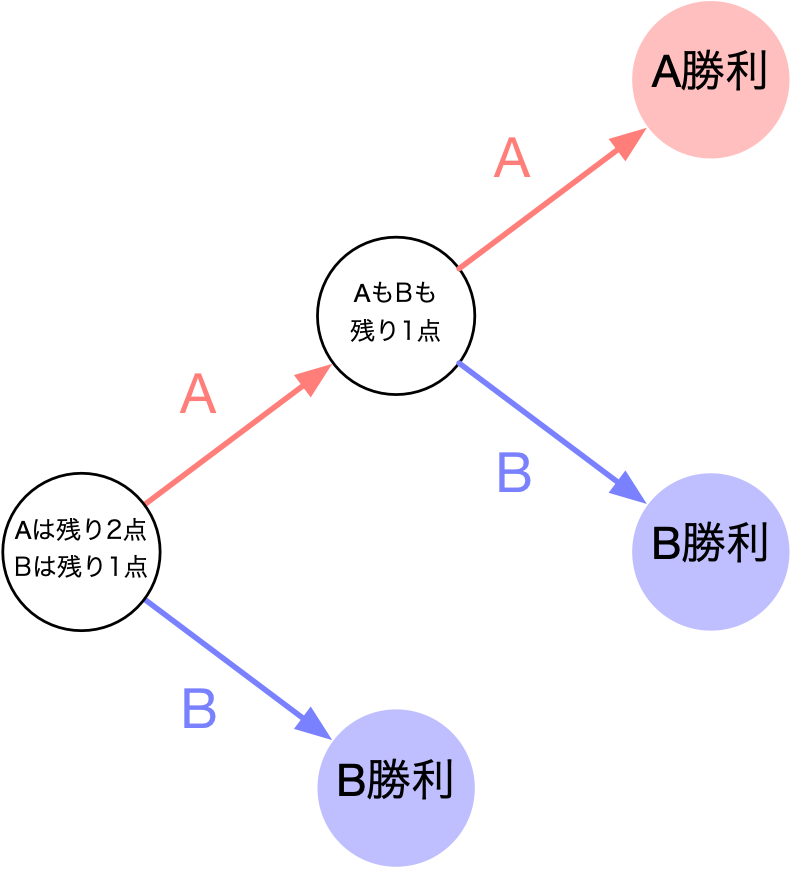
僕「うんうん! それは僕もやったよ。 一歩一歩まちがっていないことを確認しながら、式を作る。 式を変形する。式を確かめる。そういうことだね」
テトラ「はい、そうです。あたしは式を読みながら、何かこう《具体的なもの》をいじっている感じがしました。 左辺に出てくる $p(\UL2,1)$ の $\UL2$ は《残り $\UL2$ 点で $A$ が勝つ》ということを表している $\UL2$ です。 その $2$ は右辺になると $p(\UL1,1)$ のように $\UL1$ に変わります。 これは《残り $\UL1$ 点で $A$ が勝つ》状況に変化したことを表していますよね」
僕「そうだね」
テトラ「そこであたしは、 $A$ に $1$ 点をあげた気持ちになりました。具体的に」
僕「なるほど、なるほど。テトラちゃんはちゃんと式を扱っているんだね。 $A$ の得点が $1$ 点プラス」
テトラ「……ちょっとお待ちください。他の場合もそうなってるわけですよね。たとえばさっき計算した $p(1,2)$ です(第259回参照)」
$$ p(1, 2) = \frac34 $$僕「うん、そうだね。 $p(1, 2)$ の場合も図をなぞっている感じがするね」 こうなるから」
$$ p(1, 2) = \frac12 + \frac12p(1, 1) $$$p(1, 2)$ を考えるときの状況
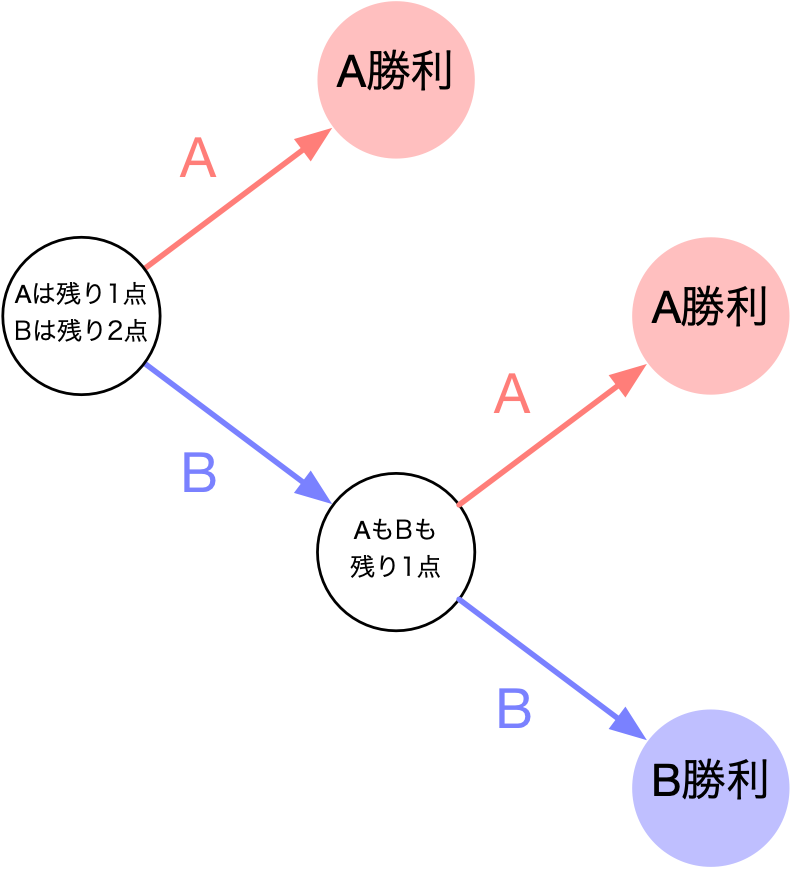
テトラ「ははあ、確かにそうですね。この式は二つの数の和ですが、それぞれちゃんと対応しているものがあります!」
$$ p(1, 2) = \underbrace{\frac12}_{\REMTEXT{$A$が出る}} + \underbrace{\frac12p(1, 1)}_{\REMTEXT{$B$が出る}} $$僕「そうそう。その《$B$ が出る》方は、 $\frac12p(1,1)$ になっている。 $A$ も $B$ も残り $1$ 点という状況に対応していることになるね」
テトラ「先輩! あたし、当たり前のこと言ってもいいですかっ!」
僕「もちろん……どうぞ」
テトラ「ここで和が出てくるのは、排反だからですよね。 コインを $1$ 回投げるとして、 $A$ が出るのと $B$ が出るのは排反な事象です。 だから、 $$ p(1, 2) = \FBOX{\frac12} + \FBOX{\frac12p(1, 1)} $$ の右辺は二つの和の形になる」
僕「そうだね。それでいいよ。少し補足すると、コインを $1$ 回投げて、 《$A$ が出た上で、その先 $A$ が勝つという事象》と《$B$ が出た上で、その先 $A$ が勝つという事象》に対応しているかな」
テトラ「あ、はい。あたしが言いたかったのもそういうことでした。あれ、でもこの二つの式だと……?」
$$ \begin{align*} p(2, 1) &= \frac12p(1, 1) \\ p(1, 2) &= \frac12 + \frac12p(1, 1) \\ \end{align*} $$テトラちゃんはそこで無言になる。そして、しばらく爪を噛みながら式をじっと見続けた。
何か、変わったことに気付いたんだろうか。
僕「……」
テトラ「この二つの式はどちらも、まちがっていないのに、変なことがあります」
僕「どこが変だろう」
テトラ「$p(2,1)$ と $p(1,2)$ では $A$ と $B$ の残り点数が入れ替わっているだけで対称です。 でも、右辺を見ると、対称になっていません」
$$ \begin{align*} p(2, 1) &= \frac12p(1, 1) \\ p(1, 2) &= \frac12 + \frac12p(1, 1) \\ \end{align*} $$僕「ああ、それは簡単に説明がつくよ。 $p(a,b)$ というのは 《$A$ が残り $a$ 点で $B$ が残り $b$ 点という状況で、 $\UL{A}$ が勝つ確率》 なんだから、概念として非対称になってる。だから式が対称でなくてもおかしくはないよ。 $A$ が勝つ確率の方に注目しているんだから」
テトラ「なるほど、そうですね……ちゃんと式が表しているものを考えるべきでした」
僕「うん、式の対称性にこだわるんだったら、こんな書き方をしたらとても気持ちがいいよ。 $0$ と $1$ に注目」
$$ \begin{array}{rll} p(2, 1) &= \dfrac12\cdot p(1, 1) &+ \dfrac12 \cdot \UL0 \\ p(1, 2) &= \dfrac12\cdot \UL1 &+ \dfrac12 \cdot p(1, 1) \\ \end{array} $$テトラ「これは……?」
僕「意味わかる?」
テトラ「……ああ、わかりました。 $0$ は《$B$ がもう勝利を決めたので、 $A$ が勝つ確率は $0$》のところ。 それから $1$ は《$A$ がもう勝利を決めたので、 $A$ が勝つ確率は $1$》のところですっ!」
僕「そういうこと。こんなふうに $0$ と $1$ を明示的に書いてやれば、 テトラちゃんが言ってた《変なこと》はなくなると思うんだけど」
テトラ「納得です! 式って不思議ですね」
僕「うん、そうだ。さらにこんなふうにすると、もっと気持ちがいいんじゃないかな」
$$ \begin{align*} p(2, 1) &= \frac12\cdot p(1, 1) + \frac12 \cdot \UL{p(1, 0)} \\ p(1, 2) &= \frac12\cdot \UL{p(0, 1)} + \frac12 \cdot p(1, 1) \\ \end{align*} $$テトラ「え……これは?」
僕「うん。 $p(1, 0) = 0$ で $p(0, 1) = 1$ と定義して、 $0$ や $1$ という数の意味がはっきりするようにしたんだよ」
テトラ「先輩、でもそれはおかしいです。だって問題文には条件があって、 $p(a, b)$ で $a$ と $b$ は正の整数でなければいけません。 だったら、 $p(1, 0)$ や $p(0, 1)$ のように $0$ になってはまずいのではないでしょうか」
僕「そうだね。だから、僕たちはいま関数 $p(x,y)$ の定義域を拡張して考えたことになる」
テトラ「拡張……」
僕「問題文で $a$ と $b$ を正の整数として考えたのは、 $0$ にして考える意味がないから。 だって《残り $0$ 点で $A$ が勝つときの確率》なんて実際の問題としては考える意味がないからね。 いや、意味はあるんだけど、答えが当たり前すぎるということ」
テトラ「意味はあるけど、意義はない?」
僕「まあ、そんな感じ。でも $p(1, 0) = 0$ と定義して、 $p(0, 1) = 1$ と定義することは、 関数 $p(x, y)$ の定義域を拡張する方法としては悪くない。一貫性があるからね」
テトラ「ええと、その一貫性というのは?」
僕「$p(1, 0) = 0$ というのは 《$A$ が残り $1$ 点、 $B$ が残り $0$ 点という状況で $A$ が勝利する確率》 として読んでもおかしくないということ。 $A$ はもう負けているから勝利する確率は $0$ になる」
テトラ「ああ、確かにそうですね。 $p(0, 1) = 1$ の方は逆です。 《$A$ が残り $0$ 点、 $B$ が残り $1$ 点という状況で $A$ が勝利する確率》 は $1$ に等しいです。だって、もう $A$ は勝ってますから!」
僕「そうだね。さっきは答えが当たり前すぎて意義がないといっちゃったけど、 でも式を考える上では大いに意義がある」
テトラ「はい。この式はとても、とても納得できます! すべての場合を尽くしている感じがします」
$$ \begin{align*} p(2, 1) &= \frac12\cdot p(1, 1) + \frac12 \cdot p(1, 0) \\ p(1, 2) &= \frac12\cdot p(0, 1) + \frac12 \cdot p(1, 1) \\ \end{align*} $$僕「あ、そうそう。いま新たに定義した $p(1, 0)$ と $p(0, 1)$ を使うと、 簡単に計算できた $p(1, 1)$ もさらにすっきり表せるよ」
テトラ「$p(1, 1)$ は $\frac12$ ですよね。コインを投げて $A$ が出れば $A$ の勝利ですから」
僕「そうなんだけど、この式を見て」
$$ \begin{align*} p(1, 1) &= \frac12\cdot p(0, 1) + \frac12 \cdot p(1, 0) \\ &= \frac12\cdot1 + \frac12\cdot0 \\ &= \frac12 \end{align*} $$テトラ「なるほど……確かに納得です。 あたしは《コインを投げて $A$ が出れば $A$ の勝利》とだけ考えましたが、 $$ p(1, 1) = \frac12\cdot p(0, 1) + \frac12 \cdot p(1, 0) $$ という式はもっと状況をきちんと表していますね……つまり、 《$A$ が出て $A$ が勝利する事象》と《$B$ が出て $A$ が勝利する事象》という排反な事象です。 もっとも、《$B$ が出て $A$ が勝利する事象》は起きないんですけれど」
僕「そうそう。テトラちゃんはよく理解しているよね」
テトラ「先輩はいつもあたしのことを励ましてくださいます。ありがとうございます」
僕「テトラちゃんはがんばっているもんね。それで、と……だいぶ《お友達になれた》かなあ?」
テトラ「お友達!……そんな恐れ多い。でも、仲良くしていただけるのはありがたいです」
テトラちゃんはそういって頭を下げた。
僕「え? いや、関数 $p(x, y)$ のことはよくわかったかなあ、というつもりで言ったんだけど」
テトラ「え……えっ、あっ、もしかして《お友達》って、関数 $p(x,y)$ のことですかっ!……お恥ずかしい」
僕「いやいや、僕の方こそ、仲良くしてくれるの、ありがとう」
テトラ「いっ、いえっ!……恐縮です」
僕「テトラちゃんがていねいに式を読んでくれたから、僕たちは関数 $p$ を拡張することができたね」
テトラ「は……はい」
僕「これでそろそろ、関数 $p$ の性質をつかまえることができたと思う。関数 $p$ はこんな漸化式を満たしている」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2019年5月10日)
この記事は『数学ガールの秘密ノート/確率の冒険』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!