第259回 シーズン26 エピソード9

確率の冒険：未知を求めて（前編）

図書室にて

僕「テトラちゃん？」

テトラ「あっ、先輩！　ちょうどいいところに！　ちょっとご相談に乗ってください。この問題なんですが……」

僕「ああ、これは有名な確率の問題だよね。メレの問題だ」

テトラ「あっ、まだ問題は途中です」

僕「もう先も分かるけど……あ、いや、ごめんごめん。最後までちゃんと聞くよ」

テトラ「はい。では改めて……」

僕「うん、やっぱりメレの問題だ」

テトラ「そんなに有名な問題なんですか」

僕「そうだね。何しろ確率というものを正確に分析しようとした歴史的な問題だから。 メレの問題、未完のゲームの問題、得点の問題など、いろんな名前がある。 もっとも、問題自体はメレが考えたわけではなく、もっと前からあったんだよ」

テトラ「そうなんですね」

僕「メレというのは当時有名なギャンブラーで、 この問題と本質的に同じ問題をパスカルに尋ねた」

テトラ「パスカルさんに確率の計算をしてもらったわけですか」

僕「そうなんだけど、確率の計算とは思ってなかっただろうね」

テトラ「どうしてでしょう」

僕「《確率》という言葉はパスカルが生きている時代にはまだなかったからだよ」

テトラ「ああ……！」

僕「つまり、運や偶然というものをどうすれば系統だてて考えることができるか、はっきりしなかった。 パスカルは答えを出すことができたけれど、 不安だったのでフェルマーに手紙を書いた。 その手紙のやりとりが、確率が数学になっていくための大きな一歩となった……というくらいしか僕は知らないなあ」

テトラ「フェルマーさんって、あのフェルマーさん？」

僕「そう、フェルマーの最終定理のフェルマー」

テトラ「そんなものすごい問題だったんですね、これは！」

僕「うん。理論がない時代に理論を作るのはとてつもなく大変だったと思うよ。 でも、僕たちはもう整備された確率を学んでいるから、 問題1はそれほど難しくないよ。 ただ、問題1のままだと数学の問題としては難点があると思う」

テトラ「難点といいますと？」

僕「$A$ と $B$ は賞金をどれだけの割合で受け取るのが妥当かというのは、 数学の問題としては明確じゃないから。 もちろん、《妥当》をどんなふうに決めるかまで考えることは、現実の問題としては意味があるね」

テトラ「……ちょっとよくわかりません」

僕「あ、いや、そんな難しい話じゃないよ。どういう割合で分けるかというのは、 必ずしも一つの方法に決まるわけじゃないよね。 $A$ は $2$ 点取り、 $B$ は $1$ 点取った。ではどう分配するのが《妥当》か。 たとえば、 $A$ はこう主張するかもしれない」

テトラ「あっ、でも、それはひどいですよね。だって未来はわかりませんから。もしかしたらこの後 $B$ がぽんぽんと $2$ 連続で得点するかもしれません」

僕「もちろん、そうだね。でも $A$ の言いたいこともわかる」

テトラ「そうですけど……」

僕「得点が高い方が総取りするという決め方もできないわけじゃない。 でも、そういう決め方だと、じゃあ両方とも同点だったらどうするのかという問題は残る」

テトラ「同点だったらちょうど半分ずつにしたいです」

僕「そうだよね。だから、結局、何が妥当かを決めた上でないと計算はできない。 もしかしたら $B$ はこういうかもしれない」

テトラ「……それは、反論しにくい主張ですね。だって確かに $A$ は $2$ 点、 $B$ は $1$ 点を確かに取っています。それはゆるぎない事実です。 ですから、そのゆるぎない事実をもとにして分配する気持ちはわかります」

僕「でも、じゃあ、もしも $A$ が $1$ 点、 $B$ が $0$ 点で中断するとなったら、 $A$ が総取りでいいのかというと疑問は出てくるよね」

テトラ「そう言われればそうですね。やはり《妥当》を明確に定めないといけません」

僕「だよね」

テトラ「ではどうすれば」

僕「この問題を数学の問題として解くとき、《妥当》な分配の割合はこう考えることが多いんじゃないかな。 仮にゲームを中断せずに継続したとするならば、勝利する確率はそれぞれどれだけあるかを計算する。 そして、勝利する確率の比にしたがって賞金を分配する」

テトラ「それはとてもよくわかります。でも、その方法の妥当性はどこから来るんでしょう……だって、未来はわかりませんよね」

僕「そうだね。確率はいわば未来の計算をしていることになる」

テトラ「未来の計算……確かにそういう感じはしますが」

僕「この問題では《$A$ が $2$ 点とり、 $B$ が $1$ 点とった》という状況が出てくる。 仮にこの状況を《$Q$ の時点》と呼ぶことにしよう。 でも、もしも《$Q$ の時点》で中断せずに続けたとすると、あるときは $A$ が勝つかもしれない。あるときは $B$ が勝つかもしれない。 何度も何度も《$Q$ の時点》に戻ってきてゲームを行ったとすると、 $A$ と $B$ が勝つ割合はどうなるだろうか」

テトラ「なるほど、その割合が確率！」

僕「うん、その割合を確率だと考えることができる。 《$Q$ の時点》に何度も何度も戻らなくてもいいかな。 《$Q$ の時点》で、ものすごくたくさんの可能な世界に分かれて、 そのうちの何割の世界で $A$ が勝つかを考えるともいえる。 SFっぽくなってきたけど」

テトラ「でも、よくイメージできます。いわば賞金を可能な世界すべてにばらまいたようなものです」

僕「ただ、これは確率そのものというよりも、それをどう解釈するかという話だから、 数学とは離れた議論のような気もする」

テトラ「ということは、こんなふうに問題を書き換えてしまえば明確になりますね」

僕「ああ、そうだね。問題2で得られる $P(A)$ を使えば、 $B$ が勝利する確率も $P(B) = 1 - P(A)$ で得られる。 確率の比を使って賞金を分配することが妥当だと仮定すると、 問題1の解答は、 $P(A):P(B)$ で得られるわけだ」

テトラ「そうですね」

僕「じゃあ、いっしょに問題2を解いてみようか」

テトラ「いえ、実はもう、あたし、これと同じ解釈で解いているんです」

僕「えっ、あれ、そうだったの。てっきりこの問題を解いて欲しいという意味かと思ったよ。 何だか僕は早合点ばかりしているなあ」

テトラ「いえいえ、ご相談したいことはもっと先にありまして……まずは、 あたしのこの解答を見てください」

僕「うん、とても整理されていてわかりやすいよ」

テトラ「はい、でも、恥ずかしながら、これは最終形態なんです」

僕「最終形態」

テトラ「考えている最中はもっとぐちゃぐちゃなことになっていました。 最初は頭の中で、最初に $A$ が出たら $A$ がプラス $1$ になる。 $B$ が出たら $B$ がプラス $1$ になるけどそこでは勝負はまだつかなくて……と、 場合分けの場合分けでぐるぐるしちゃいました。 でも、それは頭の中だけでやろうとしたのが悪かったんです」

僕「なるほどね」

テトラ「頭の中だけでやるのではなく、場合分けの樹形図をちょっと描くだけで明確になりました。こんな図です」

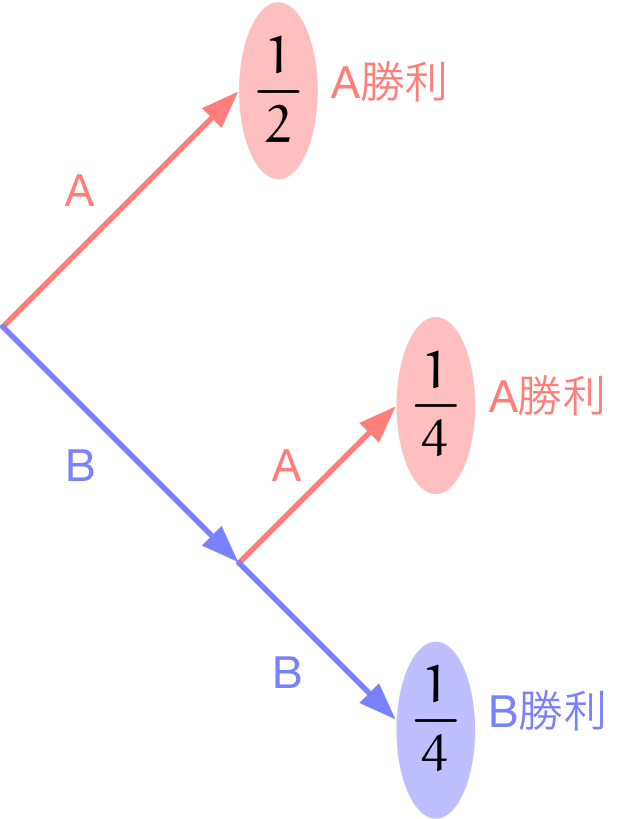
僕「そうそう、そうだね。紙に書いて整理するだけではっきりする。 なんだ、そういうことかってね」

テトラ「あたし思ったんですが、このような樹形図でも、条件付き確率のときに書いた表でも、 どちらも《全体とは何か》を知るためにあるんですよ」

僕「ははあ？」

テトラ「先輩、おっしゃってましたよね。あたしが《全体とは何か》を誤解していたということ（第257回参照）」

僕「うん」

テトラ「あれから、注意するようにしているんです。問題に書かれていることの一部分だけじゃなくて、 《全体とは何か》を考えるように」

僕「それはすごいよ、テトラちゃん！」

テトラ「……ところがです。ご相談したいことというのはここからなんです」

僕「おお？」

テトラ「あたし、この確率の問題を解くことはできました。 $A$ が $2$ 点で、 $B$ が $1$ 点取った状況で中断した場合の話です。 $P(A) = \frac34$ となりました」

僕「そうだね」

テトラ「あたしは先輩がいつもおっしゃる《一般化》をしたいと思ったんです！　つまり、このような問題を考えてみよう！と……」