![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/確率の冒険』として書籍化されています。
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
僕とユーリは確率についてのおしゃべりをしている。
確率を定義するという話題から、 コインについての疑問へ移ってきた(第251回参照)。
ユーリ「……でも、具体的なコインで《表が出やすいかどうか》を調べる方法がないなら、 結局確率は、実際の役には立たなくなるじゃん!」
僕「ユーリは賢いなあ! そうだね。 具体的なコインについて《表と裏でどちらかが出やすいことはない》という仮定を満たすかどうかわからないなら、 意味がなくなる。でも、調べることはできるんだ」
ユーリ「さっき調べる方法ないって言った……」
僕「仮定を満たすと断言することはできないんだ。 でも、仮定を満たしそうかどうかはわかる」
ユーリ「へえっ! そんなことわかんの?」
僕「何回も投げてみればいい。実際に」
ユーリ「は? 何その原始的方法。実際に投げて、何がわかるの?」
僕「原始的方法というけど、僕たちがコインに対して出来るのは《投げてみる》しかないんだから、 原始的も何もないよね。投げてみて表が出るかどうかを調べていく。そうすれば……」
ユーリ「またわかんなくなった! ねーお兄ちゃん、いま知りたいのは具体的なコインで、表と裏が同じように出やすいかどうかだよね?」
僕「そうだね、その通りだよ。だから投げてみて……」
ユーリ「待って待って待って。コインを投げて起きることはわかってるじゃん。 表が出たり、裏が出たりする。でもどちらが起きるかはわからない。 どんだけ注意しても、どちらが起きるかはわからない。 それははっきりしてる。なのに、何かわかることがあるの?」
僕「こうするんだよ。何回も投げてみて、表が何回出たかを数えるんだ」
ユーリ「うーん……ユーリも、うすうす思ってたよ。《数える》のかなって。 ほんとだよ。でもすぐキャッカしちゃった」
僕「却下?」
ユーリ「だってね。数えても、やっぱりバシッと決まるわけじゃないもん。 表が出るか、裏が出るか、はっきりしないもん。 起きたり起きなかったりすることについて、 はっきり言えることなんて何もないはず」
僕「なるほどね。ユーリの気持ちはよくわかるよ。 さっきも言ったけど、目の前にあるコインについて、 表と裏でどちらかが特別出やすいかどうかを断言することはできない。 でも、どちらも同じように出やすいらしいということは判断できるんだよ」
ユーリ「うーん……」
僕「話を整理しよう。《表が何回出たかを数える》ということをもう少しちゃんといえば、こうなる」
《コインを繰り返し投げて、表が出る回数を数える》
コインを投げる回数を正の整数 $M$ で表すことにする。
コインを $M$ 回投げる。
$M$ 回のうち、表が出た回数を $m$ で表す。
ユーリ「えーと、これがどーしたの?」
僕「こんなふうに $M$ や $m$ のように表すことにすると、 話があいまいにならないからね」
ユーリ「いやいや、ユーリはごまかさられあさ……ごまかされませんぜ」
僕「噛むなよ」
ユーリ「ごまかされませんぜ。文字を使っても、何もはっきりしてないもん。 だって、コインを $M$ 回投げたとき、表が出た回数を $m$ としても、 $m = 0$ かもしれないし、 $m = M$ かもしれない。何もはっきりしていない」
僕「その通りだね。たとえば $M = 2$ だとすると、次の $4$ 通りがあることになる」
ユーリ「ふんふん?」
僕「一回目が……とか、二回目が……というのは面倒だから、単に表裏を並べて表すことにしよう」
ユーリ「まーそだね」
僕「いまは $M = 2$ で考えたけど、 $M = 3$ なら、こうなる」
ユーリ「ははーん……読めてきたよん。 $M$ を大きくしていくつもりなんでしょ。 投げる回数を増やしていったら、 投げる回数のちょうど半分が表になるだろ?……みたいな話。 $M$ の $\frac12$ が $m$ だろって?」
僕「そうだね。だいたいはそういう話なんだけど、ちょっと違う。投げる回数のちょうど半分になる可能性は減っていくから」
ユーリ「?」
僕「それに、たとえば $M$ が奇数だったら、ちょうど半分が $m$ になることは絶対にないよね。 $3$ 回投げたときに $1.5$ 回表が出るなんてことは絶対に起きない」
ユーリ「あー……」
僕「もうちょっと進めよう。 $M = 4$ ならこうなる」
ユーリ「お兄ちゃん、お兄ちゃん。これ、 $M$ を増やしていったらとんでもないことが起きるヤツじゃない? 倍々ゲーム」
僕「そうだね。すべての場合を列挙していたら、 $M$ が大きいときに爆発的に長くなってしまう。 だから、表現の仕方を工夫しよう。《表が何回出るか》に注目して、そのパターンを数えるんだ」
ユーリ「パターンを数える?」
僕「たとえば、 $m = 4$ になるパターンは、表表表表しかない。 $1$ 通りだね」
ユーリ「あー、そーゆー意味ね。 $m = 3$ になるのは、表表表裏と、表表裏表と、表裏表表と……あと、裏表表表の $4$ 通り」
僕「そういうことだね。 $M = 4$ のとき、こんなふうに整理できる」
ユーリ「なーるほど」
僕「$1, 4, 6, 4, 1$ だね」
ユーリ「そだね……って、これパスカルの三角形に出てくる数じゃん!」
パスカルの三角形に出てくる $1,4,6,4,1$
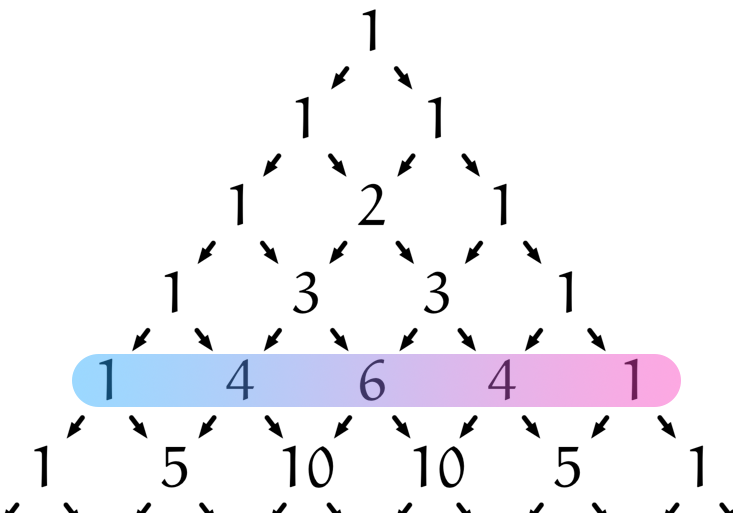
僕「その通り!ユーリの発見はすばらしいな」
ユーリ「は? これ偶然?」
僕「そんなことないよ。コインを $M$ 回投げたときに出てくる可能性のあるすべてのパターンを調べて、 表が出る回数で整理すると、パスカルの三角形の $M$ 行目に出てくる数列になる。一番上を $0$ 行目としたら、だけど」
ユーリ「なんでっ! ……んんん? 当たり前?」
僕「わかってしまえばあたりまえだね」
ユーリ「これってあれでしょ。場合の数の問題。道の個数になる! 左下に進むのが表で、右下に進むのが裏」
パスカルの三角形と場合の数
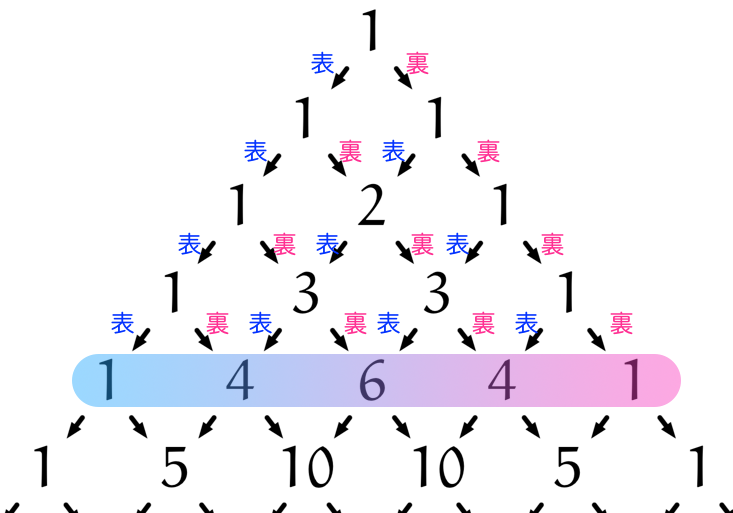
僕「ああ、そうだね。いろんな考え方があるけど、 たとえば表が $3$ 回出るパターンは、こんな $4$ 通りの道に対応しているよね」
表→表→表→裏
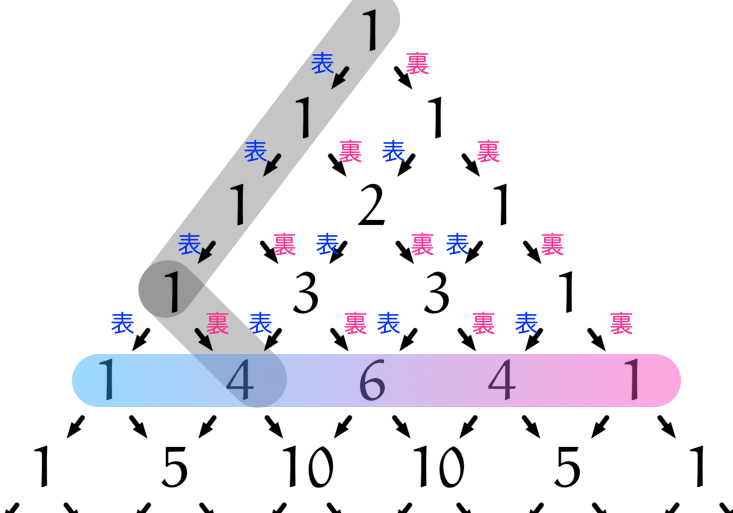
表→表→裏→表

表→裏→表→表
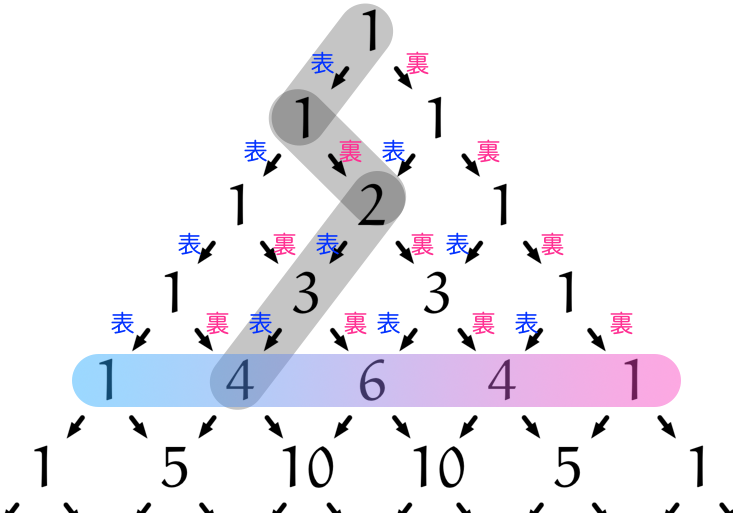
裏→表→表→表

ユーリ「……ちょっと待って。いまコイン投げの話をしてたんでしょ。パスカルの三角形はいーんだけど、確率はどーなった?」
僕「パスカルの三角形の話、したいんだけどな」
ユーリ「やだ。パスカルの三角形は計算すれば出るのがわかるもん。コインの話のもやもやの方をちゃんとしたい!」
僕「はいはい。えーと……」
ユーリの要望に従って、僕は話の順序を再検討する。
二項分布の話に進むのはやめて……と。さて、それじゃあどうしようか。
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2019年3月8日)
この記事は『数学ガールの秘密ノート/確率の冒険』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!