![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。 好奇心旺盛で根気強い《元気少女》。言葉が大好き。
僕が図書室にいくとテトラちゃんがノートに向かっていた。
僕「テトラちゃん、今日はどんな問題を解いているの?」
テトラ「あ、先輩! 問題といいますか……問題なんでしょうか?」
僕「何か書いてたよね」
テトラ「ええ、これです」
テトラちゃんのノート
$$ f(x) = f(a) + f'(c)(x - a) $$
僕「ああ、このあいだの《平均値の定理》だね(第223回参照)」
テトラ「やっぱり、すぐにおわかりになるんですね……」
僕「だって、そうだよね。ちょっと式の形は違うけど。 このあいだは、閉区間を $[a,b]$ で書いていたし、分数の形で書いてた」
$$ \frac{f(b) - f(a)}{b - a} = f'(c) $$
テトラ「はい、そうですね。ですから《平均値の定理》の式の両辺に $b - a$ を掛けて、 $f(a)$ を移項して、それから $b$ を $x$ に変えたら、さっきの式になります」
$$ \begin{align*} \frac{f(b) - f(a)}{b - a} &= f'(c) && \REMTEXT{平均値の定理}\\ f(b) - f(a) &= f'(c)(b - a) && \REMTEXT{両辺に$b - a$を掛ける}\\ f(b) &= f(a) + f'(c)(b - a) && \REMTEXT{両辺に$f(a)$を加える}\\ f(x) &= f(a) + f'(c)(x - a) && \REMTEXT{文字$b$を文字$x$に変える}\\ \end{align*} $$僕「そうだね。それで、この式変形は……」
テトラ「は、はい。これは村木先生から教えていただいたんです。 先日のロルの定理や実数の話などをレポートにまとめて持っていったとき」
村木先生は、僕たちの数学教師。 僕たちは自主的に数学のレポートを持っていくことがある。 テトラちゃんは、 先日僕たちが取り組んでいた《平均値の定理》→《ロルの定理》→《デデキントの公理》といった話をレポートにして持っていったんだろう。
僕「ああ、なるほどね。《平均値の定理》を別の方向から調べてみようという謎かけだ」
テトラ「そうなんですね。テトラは鈍くて、 そもそもこの式が《平均値の定理》だと気付くのに時間が掛かってしまいました」
僕「うん、これは僕もやったことがあるよ。とても《楽しい話》があるんだ、あのね」
テトラ「だ、駄目ですようっ! まず、あたしが考えていたことをお聞きください」
僕「そうだね。ごめんごめん。テトラちゃん、どうぞ」
テトラ「と、いっても第一歩目からあたしは大混乱しているのですけれど」
僕「この式を考察したんだよね」
テトラちゃんのノート
$$ f(x) = f(a) + f'(c)(x - a) $$
テトラ「はい、そうです。 村木先生がわざわざ $b$ を $x$ に変えたのにあたしは意味があると思いました。 つまり、この $x$ を変数だと考えたらどうかというアドバイスだと思ったんです」
僕「先生は何か解説してくれたの?」
テトラ「い、いえ。あたしがレポートを持っていって《平均値の定理》を少し話したら、 先生はにこにこして、こんな式はどうだろうとおっしゃっただけです」
僕「なるほど」
テトラ「あたしは、この式 $f(x) = f(a) + f'(c)(x - a)$ を見て、 $x$ が変数だとしたらどうなるかを考えてみました。 $x$ は実数で、値をいろいろ変えます。 $f(x)$ は $x$ の関数ですから $f(x)$ の値もいろいろと変わります」
僕「まあそうだね」
テトラ「でも、ここで出てきている $f(x)$ は具体的にどんな関数かはわかりませんから、 $f(x)$ の値がどんな値になるかは具体的にはさっぱりわかりません」
僕「……」
テトラ「たとえば $x^2 + x + 1$ のように具体的な関数だったらいいのですけれど、 具体的にわかっていない関数 $f(x)$ について何が考えられるだろう……と思いました。 でも、そこであたしは思い出しました。先輩とのお話ですっ!」
僕「僕? 何か言ったっけ」
テトラ「具体的な関数が与えられないと、雲をつかむような話で……とあたしが愚痴ったときに、 先輩は『与えられているよ』とおっしゃってくださいました(第226回参照)」
僕「ああ、言ったかも。条件のことだね」
テトラ「そうです、そうです。 $f(x)$ には微分ができるという条件がありました。 ですからあたしは、この式をとりあえず微分してみたんです! でも……」
$$ \begin{align*} f(x) &= f(a) + f'(c)(x - a) && \REMTEXT{平均値の定理から} \\ f'(x)&= (f(a) + f'(c)(x - a))' && \REMTEXT{両辺を微分した} \\ f'(x)&= 0 + (f'(c)(x - a))' && \REMTEXT{$f(a)$を微分したら$0$になる} \\ f'(x)&= f'(c)(x - a)' && \REMTEXT{$(x - a)$を微分……?} \\ f'(x)&= f'(c) && \REMTEXT{……???} \\ \end{align*} $$
僕「なるほどね……テトラちゃんの《大混乱》の意味がわかってきたよ」
テトラ「あたしは、先輩方とごいっしょに《平均値の定理》の証明を追いました。 実数の難しいところはまだ怪しいですけれど、 《平均値の定理》そのものはわかっているつもりでした。 でも、このちょっとした式変形を使って考えを進めようと思ったら、 いきなり $f'(x) = f'(c)$ という変なことになってしまいました。 $f(x)$ を微分した導関数 $f'(x)$ が $f'(c)$ という定数に等しいなんて、 どういうことでしょうっ!」

僕「あのね、テトラちゃん。テトラちゃんのチャレンジはすごいと思うよ。 自分が知っている数式を観察して、変形して、何か新しいことを探ろうとしたってことだよね」
テトラ「は、はい……」
僕「そのチャレンジはすごいけど、 惜しいのは数式だけを頼りにしてしまったというところ。 それはすごくあぶないんだ」
テトラ「え! でも、数学ってそこがすごいのではないんでしょうか。 先輩がよくおっしゃることですよね。数式を使って、数式だけを手掛かりに進んでいっても新しい世界が開ける……」
僕「そうなんだけど、僕がいいたいのは……うん、具体的に話すよ」
テトラ「よろしくお願いします」
僕「順を追って話そうね。出発点はテトラちゃんのノート」
テトラちゃんのノート
$$ f(x) = f(a) + f'(c)(x - a) $$
テトラ「はい」
僕「これは《平均値の定理》だとテトラちゃんは言ったし、僕もそう言っちゃったけど、 それはちょっとウソがあった」
テトラ「はい?!」
僕「《平均値の定理》の主張をするためには、 式をぼんと出すだけじゃなくて、 その式で使われている文字のことをちゃんといわなくちゃいけないから。 具体的にはこんなふうに……おっと、 $x$ という文字がかぶるからそこはちょっと注意して……」
平均値の定理
二つの実数 $a,x$ は、 $a < x$ を満たすとする。
関数 $f(\heartsuit)$ は、 $a \LEQ \heartsuit \LEQ x$ で連続とする。
さらに関数 $f(\heartsuit)$ は、 $a < \heartsuit < x$ で微分可能とする。
このとき、 $$ f(x) = f(a) + f'(c)(x - a) $$ を満たす実数 $c$ が、 $a$ と $x$ のあいだに存在する($a < c < x$)。
テトラ「で、でも、これは、あたしはわかっているつもりでした。 それに、先輩がいまお書きになったものでも、やはり、 $$ f(x) = f(a) + f'(c)(x - a) $$ という数式に変わりはありませんよね。関数 $f$ が微分可能であることに変わりはありません。 ですから、あたしは、できることをまずやってみようととりあえず微分して……」
僕「うん、その気持ちはわかるんだけど、この式に出てくる文字をよく考えてみて。 $a$ と $x$ はいま考えている区間の両端だね。では、 $c$ は?」
テトラ「それはわかります。 $c$ というのは《接点 $c$ での接線の傾き》が《両端 $a$ と $x$ とを結ぶ線分の傾き》と等しくなるところです。 《$c$ での微分係数》が《$a$ から $x$ への平均変化率》に等しくなるところ……で、いいんですよね。 だってそのような $c$ が存在することこそ《平均値の定理》ですから」
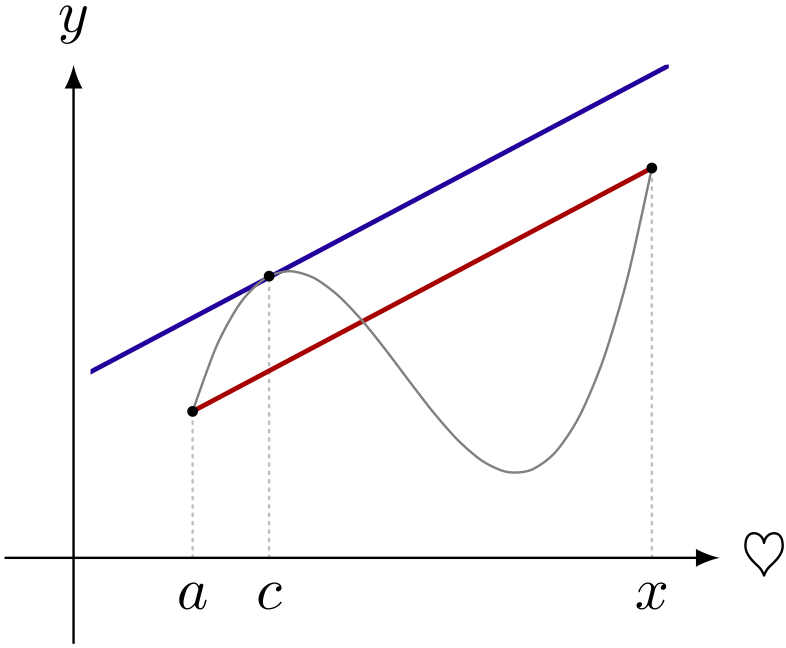
僕「テトラちゃんのその理解は百点満点だよ。 問題は、 $x$ を動かしても、 $c$ は動かないとテトラちゃんが考えたところにあるんだ。 $x$ を変数として、 $c$ を定数だと考えちゃったよね」
テトラ「……あっ!」
僕「わかった?」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2018年6月8日)