第212回 シーズン22 エピソード2

無限ポテチ（後編）

無限のイメージ

ユーリ「文字 $n$ にどんな数でもいれられるっていうのも、 無限のイメージ？」

僕「ああ、そうかも。そうだね。 あまり無限とは意識してないけど、 確かに、無限の一つの側面を表してるなあ」

ユーリ「そっか、大きくなくてもいーんだね。 大きいかどーか、は無限の一つのイメージ」

僕「そうだと思うよ。 そして、いったん誰かの心に浮かんだものを、 数学的に表現できれば、 そこについては数学で考えられるし、 議論できる。 だから、自分の心に浮かんだものを、 言葉にしようとすることは、とっても大切なことなんだ」

ユーリ「わーった。《先生トーク》炸裂だね！」

僕「茶化すなって」

ユーリ「そんで？　結局、 $\infty$ って何になるの？」

僕「何って？」

ユーリ「無限大って結局、何？」

僕「いままでその話をしてたんじゃないか。 ユーリは $1,2,3,\ldots$ の先にある無限大をイメージしたかった。 だから、 《どんな正の整数 $n$ に対しても $n < \infty$ が成り立つもの》とした。 $\infty$ はそういう性質を持つもの、とね。 そうすると、 $\infty$ は正の整数じゃないってことが証明できた （第211回参照）」

ユーリ「ふんふん。まるで読者のために書かれた《先週のあらすじ》みたい」

僕「メタ発言自重よろしく」

ユーリ「でもね、それって、 $\infty$ は正の整数ではない っていってるだけじゃん？　 $\infty$ はナントカである じゃないもん。結局、無限大って何？」

僕「なるほど。確かにユーリの主張は一理あるな。 そもそも、無限って言葉がそうだよね」

ユーリ「なに？」

僕「無限って言葉の作り方は、 《限りが無い》になってる。 《限り》とか《限界》とかいう概念を否定して初めて表現できてる。 だから、 $\infty$ は正の整数じゃないとか、 有理数じゃないとか、実数じゃないとか、 なになにじゃないという表現は、とてもしっくりくる」

ユーリ「はあ」

僕「そういえば、 英語のインフィニット（infinite）という単語も同じ作り方だ。 有限という意味のファイナイト（finite）をイン（in）で否定してる。 英語でも無限は《有限ではない》と否定的に表現してるんだね」

ユーリ「へえ」

僕「気の抜けた返事」

ユーリ「ユーリが聞いてるのは、そーゆーんじゃなくって、 数学の話なんだもん。 $\infty$ って、数じゃないとしたら、 何？」

僕「そして話はまたループに入る。 ユーリは $\infty$ をどんな性質を持つものだと考えているの？　さっきは、 どんな正の整数についても $n < \infty$ を満たすものとして考えた。 でも、ユーリはそれじゃ納得できないという」

ユーリ「納得してるよ！　でも、 まだ、 $1,2,3,\ldots$ の先にある……もの？　先に……先には何があるの？」

僕「正の整数を並べた $1,2,3,\ldots$ の先には正の整数しかないよね。 だからユーリが知りたい $\infty$ はそこにはない。 でも無限や無限大と呼べるような《何か》はないのか、ってことかなあ。 ユーリの知りたい《感じ》を言葉にしないと、 ユーリの知りたい《無限大 $\infty$》はわからないかも」

ユーリ「ぐぬぬ……どーしてもユーリが考えなくちゃならんのか。 困ったもんじゃ」

僕「年齢不詳のいとこ殿」

ユーリ「あのね、 $1,2,3,\ldots$ でヤなのは、 ずっと逃げてくからなの。遠くに。このテンテンって、 ずっと続くでしょ。 $$ 1,2,3,\ldots\ldots\ldots\ldots $$ ずっと続くから、逃げられた感じがするの。それがヤ」

僕「なるほど。確かにそれはわかるよ。 逃げられた感じ。つかまえていない感じ。 いくらつかまえても、まだ次がいるから、 逃げられている。だから《わかった感じ》がしない。 すごくよくわかる」

ユーリ「んー、だから……だから……わかんなくなった。パタリ」

僕「倒れるなよ。そうだなあ、お兄ちゃんは、漸近線を初めて習ったときに似たような感じを受けたかなあ」

ユーリ「ぜんきんせん」

僕「うん、ユーリも知ってるよね。 いちばん簡単なのは、反比例のグラフ。 $x$ を正の実数として、 $$ y = \frac{1}{x} \qquad (x > 0) $$ の関数のグラフを考えるんだ。 $x > 0$ の範囲で描くと、 グラフは双曲線を描いて、すううっと $x$ 軸に近づいていく。 $x$ 軸と $y$ 軸はこのグラフの漸近線になってる。 グラフは、いくらでも $x$ 軸に近づいていくんだけど、 決して $x$ 軸に接したり交わったりすることはない」

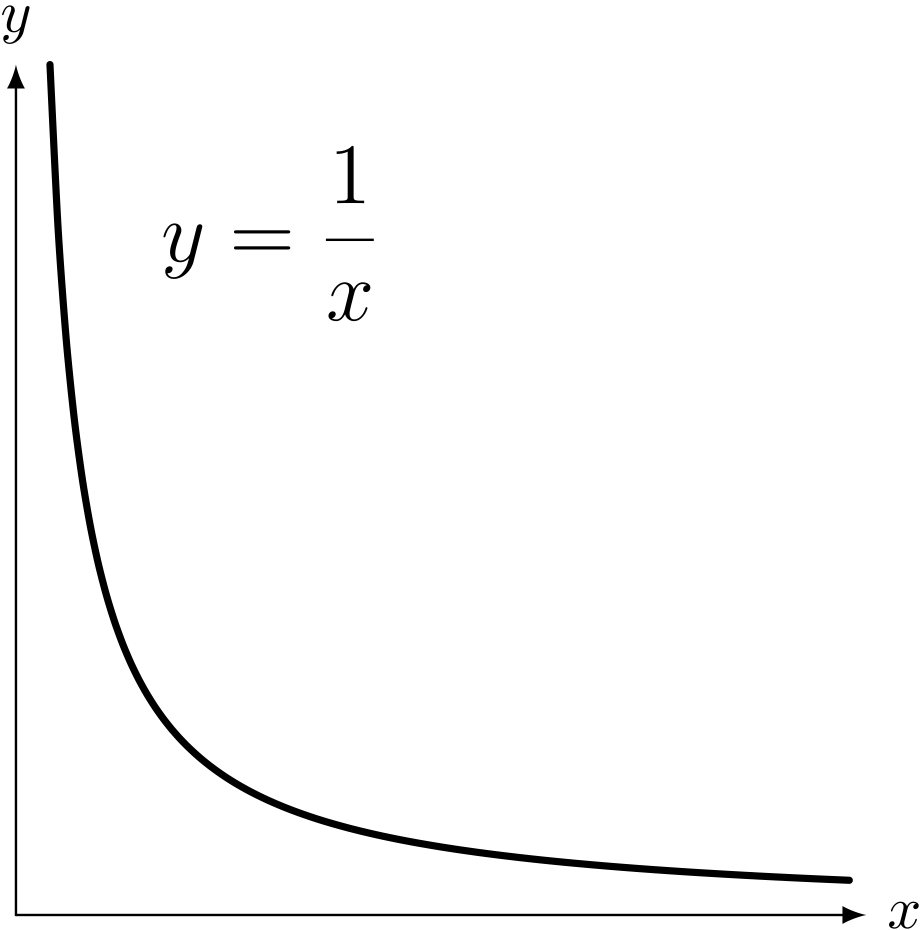
ユーリ「そだね」

僕「限りなく近づくともいえる。《限り》が《ない》んだから、 また無限だ」

ユーリ「ほんとだ。限りなく近づく……うーん、でも、 ユーリはあんまりそれ、無限って感じしない。 だって、 $x$ 軸を越えてくことはないじゃん。だったら《限りある》もん」

僕「なるほどね。確かにそれはそうだ。そのユーリの感覚はわかるよ。 この、 $$ y = \frac{1}{x} $$ というグラフに対してお兄ちゃんが無限を感じるのは、 こういうところ。 いくら小さな正の数 $\epsilon$ を持ってきて、 $\frac{1}{x}$ の減少を食い止めようとしても、 $x$ をじゅうぶん大きくしてやれば、 $\frac{1}{x} < \epsilon$ にできちゃうってところ」

ユーリ「えっ？　もっかい言って？」

僕「あ、うん。言い換えると」

ユーリ「違う！　言い換えないでいいから、 もっかい同じこと言って」

僕「いくら小さな正の数 $\epsilon$ を持ってきて……」

ユーリ「イプシロン」

僕「$\frac{1}{x}$ の減少を食い止めようとしても……」

ユーリ「ふんふんふん」

僕「$x$ をじゅうぶん大きくしてやれば、 $\frac{1}{x} < \epsilon$ にできちゃう」

ユーリ「ふんふんふんふん！」

僕「ユーリは、なにを興奮しているんだろうか」

ユーリ「こないだお兄ちゃん、極限の話をしてくれたじゃん。 《はさみうち》の話。あの話を思い出したの」

《ＣＭ》

ユーリ「ユーリといっしょに積分を見つめよう！　 『数学ガールの秘密ノート／積分を見つめて』 好評発売中！」

僕「そのキャッチコピーはどうなんだろう」

ユーリ「《はさみうち》の話は第2章に！」

僕「ああ、区分求積法でなぜ面積が求められるかという話題か。 確かに同じ話題。極限は、無限と密接に絡んでいるから」

ユーリ「$x$ をいくら大きくしても、 $\frac{1}{x}$ は絶対に絶対に絶対に絶対に $0$ になんない。 でも、 $0$ にいくらでも近づける。 確かにそう言われると無限っぽいかも。キラリーン！☆」

僕「それはユーリのひらめきの音」

ユーリ「無限、つかまえられそう！」

僕「急にどうした」

ユーリ「あのね、逆数を考えるの」

僕「逆数？」

逆数で無限をつかまえる

ユーリ「まー、お兄ちゃん、聞きたまえ。 あのね、正の整数ってこーゆーものじゃん？」

僕「そうだね」

ユーリ「正の整数って、だんだん大きくなるじゃん？」

僕「でも、ユーリは右側のテンテンが気にくわないんだろ？」