第193回 シーズン20 エピソード3

レンガを重ねて（前編）

レンガの積み方

僕「小学校に行く途中の道、公園の向かい側の角のところにレンガの家があるよね」

ユーリ「あるけど？」

僕「小学校に通ってるとき、あのレンガ塀をよく見てたんだ」

ユーリ「『少年がレンガ職人を目指したのはそのときだった』」

僕「ナレーションつけるなよ。 ……ともかく、レンガって、 こんなふうにずらして積むよね」

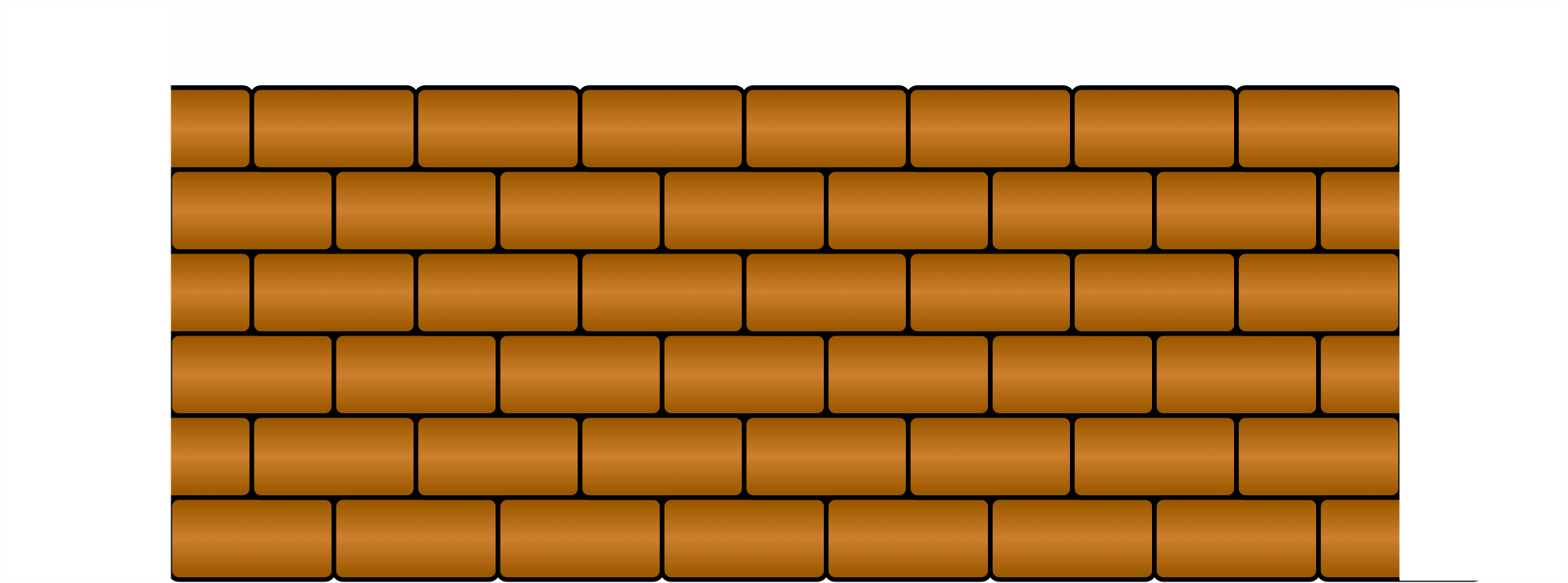
ユーリ「そだね」

僕「でも、もしかしたら、こんなふうに揃えて積むことがあるかもしれない」

ユーリ「ずらさないで積むって意味だよね。 レンガは知らないけど、ブロック塀だと、 こーゆー積み方もするかもね？」

僕「ああ、そうだね。小学校のとき、 強さの点ではずらしたほうがいいのかな……って考えてたんだ。地震対策」

ユーリ「そっかなー……見た目じゃないの？」

僕「大きさが違うレンガを使ったらどうなるかということも考えたなあ」

ユーリ「意味わかんない。大きさが違ってたらうまく積めないじゃん？」

僕「ああ、高さは一定でいいんだよ。 うまく《ずれる》ように、横の長さが違うレンガを使うってこと。 たとえば、最初の段には長さが $2$ のレンガだけを並べて、 次の段には長さが $3$ のレンガだけを並べていく……こんなふうにね」

ユーリ「あっ、そーゆー意味？　それでも、 《ずれ》がなくなるときあるよ。 ほらほら、こーゆーところ、ときどき揃っちゃうじゃん」

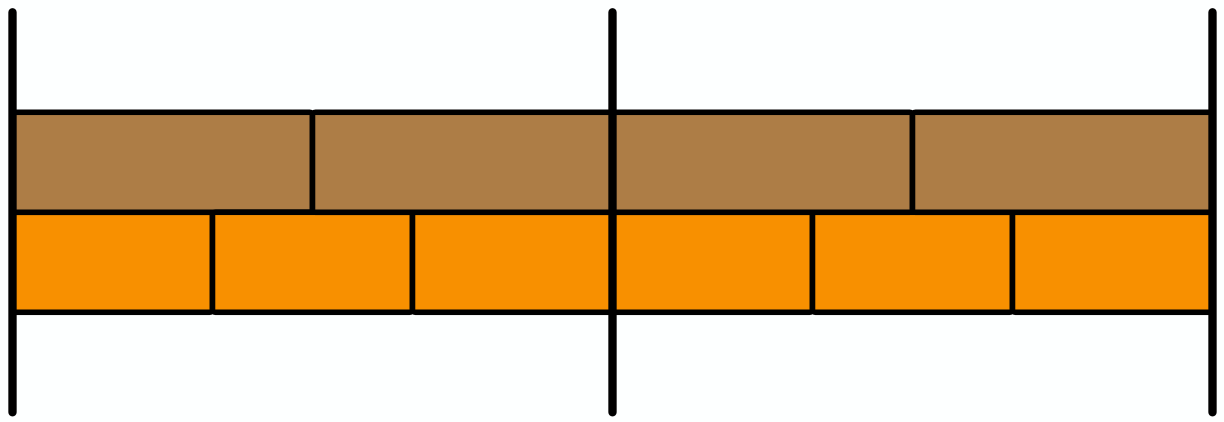
僕「そうだね、ユーリの言う通りだ。小学生だったお兄ちゃんもそれに気付いたよ。 そして、レンガが揃うところは、ちょうど公倍数だってことにも気付いたんだ。 $2$ と $3$ の公倍数になってる $0,6,12,18,\ldots$ のところで揃うんだよ」

ユーリ「ほほー！　……てか、それって、あたりまえではないでしょーか？」

僕「いや、もちろん当たり前なんだけど、小学生のときには感動したんだよ。 そして、最小公倍数の意味もよくわかった。 つまり、レンガのスタート地点を $0$ とすると、 レンガがはじめて揃うところは $6$ だ。 $2$ と $3$ の最小公倍数である $6$ のところではじめて揃うよね！」

ユーリ「ふむふむ。なるほど確かにそうじゃな。よくそれに気付いたのう……」

僕「いや、ハカセにならなくていいから」

ユーリ「そんでそんで、他にどんな発見したの？」

僕「二つの数の《積》と《最小公倍数》の違いもレンガでよくわかった。 たとえば、 $4$ と $6$ で考えてみる。 $4$ のレンガと $6$ のレンガを積んでみるんだよ」

ユーリ「$4$ を $6$ 個並べるのと、 $6$ を $4$ 個並べるのが、どっちも $24$ で揃うって話？」

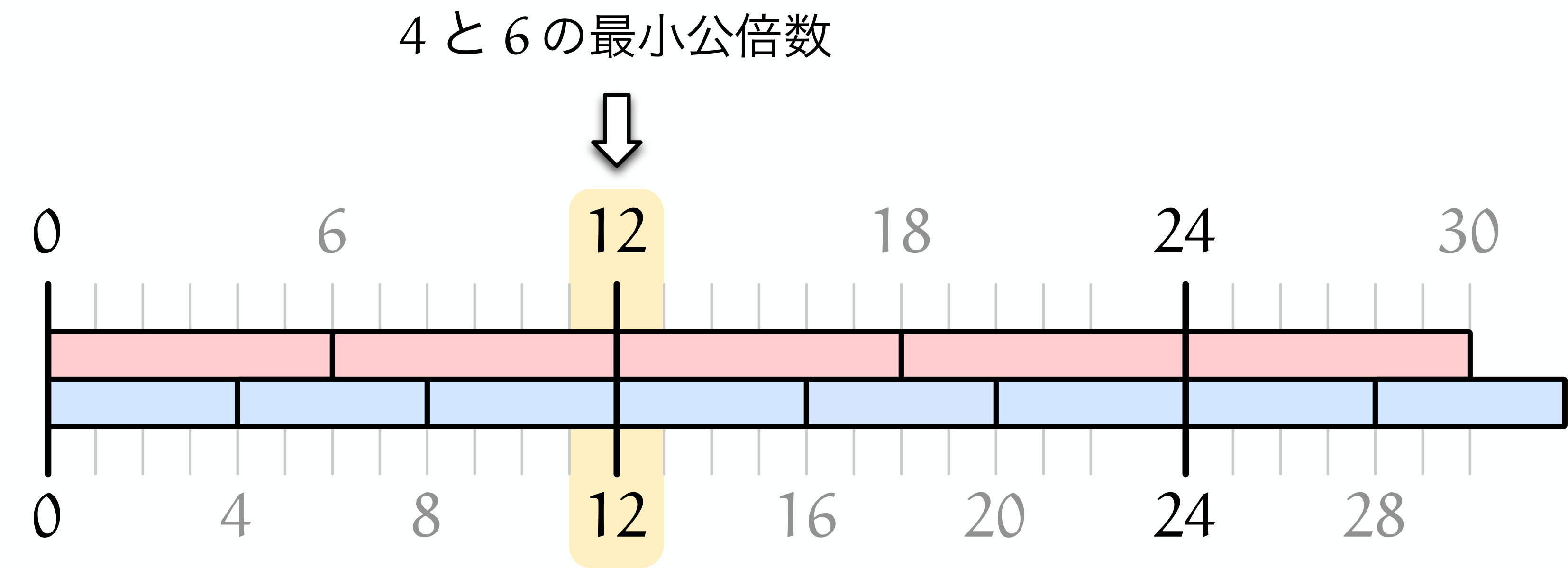
僕「そうだね。 $24$ が $4$ と $6$ の《積》で、 そこでレンガが揃うのはよくわかる。 でも《積》のところではじめて揃うときとは限らない。 $24$ に行く前に $4$ と $6$ の《最小公倍数》である $12$ で、すでに揃ってるのがわかる」

ユーリ「ふんふん。 《$4$ と $6$ の積》だと $24$ だけど、《$4$ と $6$ の最小公倍数》だと $12$ だね……あっ、 これ、さっきの話だね？　 《$mn$ の倍数》と《$m$ と $n$ の公倍数》は違うって話（第192回参照）」

僕「そうだね。 小学校でやった分数の通分。 分母の最小公倍数を作れば通分できる。 でも、実は最小公倍数を作らなくても、 両方を掛けるだけでもいいよね。要するに公倍数を作ればいいんだから。 たとえば $\frac14+\frac16$ を計算するとき、 $24$ を使っても $12$ を使ってもいい」

ユーリ「まーね。でも掛け算すると大きな数になっちゃうから計算たいへん」

僕「その代わり、最小公倍数を求める手間が掛かる……と、まあ、 そんなことをレンガを見て考えてたんだ」

ユーリ「小学生のときに？」

僕「小学生のときに」

ユーリ「ふーん……」

僕「……」

ユーリ「ふっふっふ……」

僕「戻ってきたね」

ユーリ「え？」

僕「いや、何でもない。何を考えてたの？」

ユーリ「お兄ちゃんに出すクイズ！」

僕「なるほど、最大公約数か！　これはすばらしい問題だな！」

ユーリ「でしょでしょ？」

僕「これは、小学生のときに考えたことなかったな……」

ユーリ「そんでそんで？」

僕「ユーリはもうわかったの？」

ユーリ「まーね。簡単だよん」