第176回 シーズン18 エピソード6

どう見つけたのかは問わないで（後編）

図書室にて

テトラ「それは……いま先輩がおっしゃったように、 $(\LNOT P(x)) \LOR Q(x)$ で考えればいいんですよね？」

僕「そうだね。具体的に考えると？」

テトラ「これは……《$3$ 以下》または、《$1$ より小さい、または、 $2$ より大きい》」

僕「$(x \LEQ 3) \LOR (x < 1 \LOR x > 2)$ は、もっと簡単になるよね？」

テトラ「実数全体……ですか？」

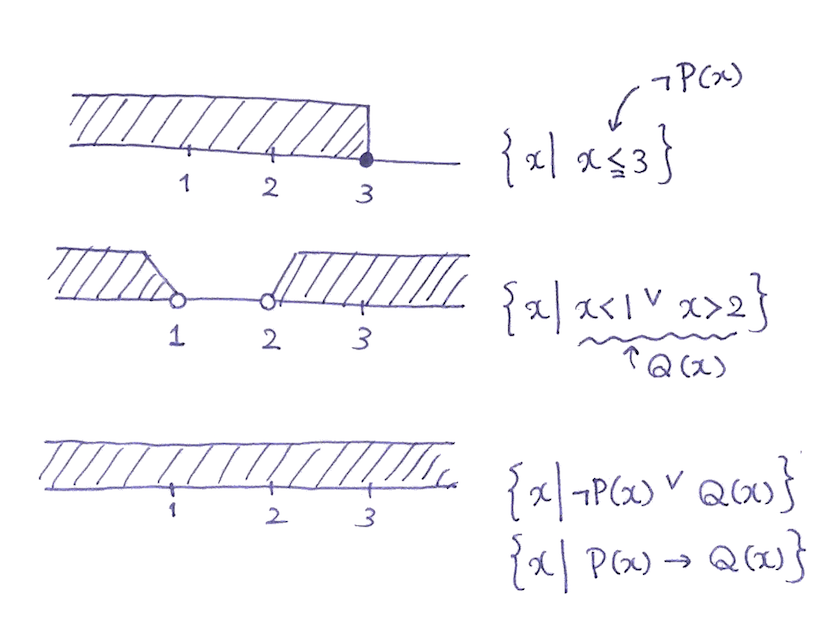
僕「そうだね」

テトラ「はい。 $1 \LEQ x \LEQ 2$ のすきま部分は、 $x \LEQ 3$ が埋めてくれますから……」

僕「うん。でね、条件 $P(x) \to Q(x)$ の真理集合を考えてみたら、 $x$ が取り得る実数全体の集合になった。 言い換えると、任意の実数 $x$ に対して $P(x) \to Q(x)$ は真になる。 つまり、《任意の》という論理の言葉と、《全体集合》という集合の言葉が対応していることになるんだね」

テトラ「なるほど……」

僕「ミルカさん、何を怒っているの？」

ミルカ「別に、怒っているわけではない」

テトラ「それは、いつもの村木先生からの《カード》ですか？」

ミルカ「……」

テトラ「これは？」

僕「これだけ？　 $f(x) > g(x)$ だけ？」

ミルカ「さすがにこれは手抜きだろう。 こういう思わせぶりな問題は……まったく」

僕「（やっぱり怒ってる）」

ミルカ「何か言った？」

僕「いや、何にも。 でも、村木先生の《カード》は思わせぶりなときや、ほのめかすときがよくあるよね。 完全な白紙のこともあった」

テトラ「これって、何なんでしょうか。不等式？」

僕「まあ、不等式だよね」

テトラ「でも、数式ですから、これは何かの問題なわけですよね」

ミルカ「ハイコンテキスト過ぎる。 $x$ は何なのか。 $f(x)$ は何なのか。 $g(x)$ は何なのか。 何をするかが語られていないのに、数式だけ与えられても問題にはならない」

僕「まあ、これが《問題》だとも書いてないけどね」

ミルカ「ふむ」

僕「でも、いつものように補って考えてみよということじゃないのかなあ」

テトラ「補う……と言いますと？」

僕「うん、だからね。文句があるなら、 自分でちゃんとした書き方をしてみようというチャレンジだと考えるんだよ」

テトラ「はあ……」

ミルカ「前向きだな」

僕「この《カード》は問題として不備だとして、 $f(x)$ や $g(x)$ は関数だという説明を書き加えて、 自分で不備じゃない問題にしてしまってもいいよね。 別に期末試験を解いているわけじゃないんだから」

テトラ「問題としての形を整えるということでしょうか」

僕「そうだね。たとえば、こんな証明をする問題はよくあるんじゃない？」

僕「実際には $f(x)$ や $g(x)$ は具体的に与えられるわけだけど。 ええと、たとえば $f(x) = x^2 + 2$ で、 $g(x) = 2x$ みたいにね」

テトラ「……」

ミルカ「ふむ。それを言うなら、これでもいい」

僕「証明問題でなくてもいいよ。こんな問題もできる」

テトラ「せ、先輩方、ちょっとお待ちください！　テトラは質問があります。 いまおっしゃった、

　　 $\REAL$ から $\REAL$ への関数

というのはどういう意味でしょうか？」

僕「ごめんごめん。 $\REAL$ というのは《実数全体の集合》のことだよ」

テトラ「あ、それはわかります。そうではなくて、 《$\REAL$ から $\REAL$ への関数》という言い回しを、 テトラははっきりと理解していないということです。 わかりにくい質問ですみません」

僕「あ、そっち？　『$f(x)$ は $\REAL$ から $\REAL$ への関数である』 というのは、

• どんな実数 $a$ に対しても、
• 関数 $f(x)$ による値がたった一つ決まって、
• しかもその値 $f(a)$ は実数である

テトラ「……」

僕「テトラちゃんは何を考えているの？」

テトラ「$\REAL$ は実数全体の集合なんですよね？　それだと、 たとえば $\sin x$ は《$\REAL$ から $\REAL$ への関数》とはいえないんでしょうか？」

僕「いやいや、そんなことないよ。だってどんな実数 $a$ に対しても、 $\sin a$ は実数値になるからね。しかも $a$ に対してたった一つ決まる」

テトラ「でも、 $-1 \LEQ \sin a \LEQ 1$ になってしまいますよね？」

ミルカ「テトラは、全射でないことを気にしているのだろうな」

僕「ああ、そうか。あのね、テトラちゃん。 $f(x)$ を《集合 $A$ から集合 $B$ への関数》といったとき、 $A$ の任意の要素 $a$ について $f(a)$ がたった一つ決まって、それは $B$ の要素でなくちゃいけない。 でも、 $B$ の要素の中には、関数 $f(x)$ の値とはならないものがあってもいいんだよ」

ミルカ「図示」

僕「はいはい……」

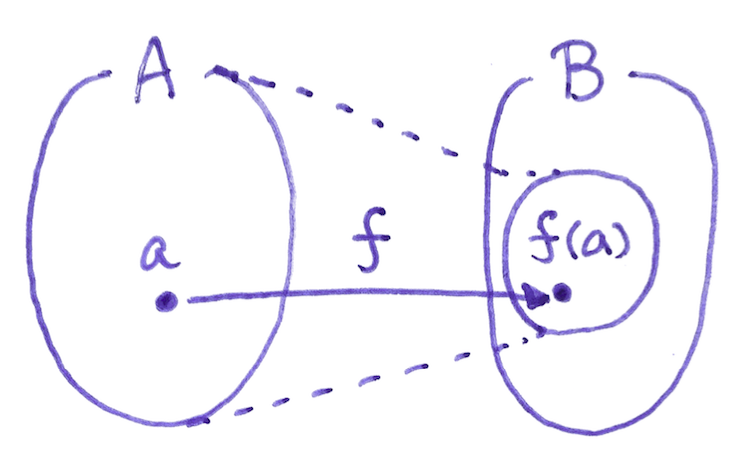
テトラ「あっ、わかりました。そうなんですね。 では、《$\REAL$ から $\REAL$ への関数》といったとき、 始めの $\REAL$ と終わりの $\REAL$ は……何といいますか、非対称なんですね」

ミルカ「一般にはそう」

テトラ「すみません、話の腰を折ってしまいました。Where were we?」

僕「$f(x) > g(x)$ という不等式があったときに、 言葉を補って、どんな問題を作れるかという話をしていたんだよね。 $f(x)$ と $g(x)$ を $\REAL$ から $\REAL$ への関数として、たとえばこんな問題が作れる。もちろん、 もっと違う問題も作れる」

テトラ「なるほどです。確かに、不等式だけでは問題にはなりませんね。 こんなに違う種類の問題が作れてしまうんですから」

僕「たとえば、(1)だと、定石としてはこういう変形をすることが多いね。同値な問題に言い換えて証明する」

テトラ「あっ、これ参考書に書いてありました。 $f(x) > g(x)$ の代わりに、 $f(x) - g(x) > 0$ を考えなさいって」

ミルカ「それは、なぜ？」

テトラ「え？」

ミルカ「なぜ、 $f(x) > g(x)$ の代わりに $f(x) - g(x) > 0$ を考えるというアドバイスがあり得るか」

テトラ「理由があるんですか？」

ミルカ「それを尋ねている」