![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
ここは僕の部屋。ユーリと僕は、論理についてのおしゃべりをしている。
僕「命題は真か偽か判断できる。真の命題と偽の命題という $2$ 通りがある。 でも、命題が多くなってくると、真と偽の組み合わせはどんどん増える。 それを整理するために真理値表(しんりちひょう)というものがある」
ユーリ「しんりちひょう」
僕「命題 $P$ は真か偽の $2$ 通りのどちらか。そのそれぞれに対して、 命題 $Q$ は真か偽の $2$ 通りのどちらか。だから組み合わせは全部で何通り?」
ユーリ「$4$ 通り」
僕「そうだね。 $2 \times 2 = 4$ 通りある。 それをこんなふうにまとめたものが真理値表」
$P\REMTEXT{かつ}Q$の真理値表
$$ \begin{array}{|cc|c|} \hline P & Q & P \REMTEXT{かつ} Q \quad \\ \hline \REMTEXT{偽} & \REMTEXT{偽} & \REMTEXT{偽} \\ \REMTEXT{偽} & \REMTEXT{真} & \REMTEXT{偽} \\ \REMTEXT{真} & \REMTEXT{偽} & \REMTEXT{偽} \\ \REMTEXT{真} & \REMTEXT{真} & \REMTEXT{真} \\ \hline \end{array} $$
ユーリ「ふんふん。これ、見たことある」
僕「まあ、よく書くからね」
ユーリ「……これって、命題 $P$ が真で、命題 $Q$ が真のときに限って、 $P \REMTEXT{かつ} Q$が真になるっていってるんでしょ?」
僕「そうだよ」
ユーリ「これって《計算》してるみたい」
僕「そうだね! その通り。その考えで合ってるよ。真と偽という $2$ つの値を使って、 《かつ》という計算をしていると考えることができる。 《真かつ真》のときだけ計算結果が真になるという計算だね」
ユーリ「んー、だったら、真理値表って、こー書いてもいいね!」
$P\REMTEXT{かつ}Q$の真理値表(書き換え)
$$ \begin{array}{|c|cc|} \hline \REMTEXT{かつ} & \REMTEXT{偽} & \REMTEXT{真} \\ \hline \REMTEXT{偽} & \REMTEXT{偽} & \REMTEXT{偽} \\ \REMTEXT{真} & \REMTEXT{偽} & \REMTEXT{真} \\ \hline \end{array} $$
僕「いいねえ!」
ユーリ「ね! 九九の表みたい! ……あ、思い出した。ほら、リサ姉のこと」
僕「リサちゃん?」
ユーリ「あのね、双倉図書館でリサ姉からお話聞いたとき、同じ計算が出てきた!」
僕「いつのことだろう……」
ユーリ「お兄ちゃんはいなかったよ。インフルインフル。双倉図書館(ならびくらとしょかん)の 《変幻ピクセル》イベント(第103回参照)」
僕「ああ、あのとき?」
ユーリ「そんときは、《ビット単位の論理積》てゆーのがあった。 《かつ》と同じだよ」
論理積(ビット単位) $$ \begin{align*} 0 \BITAND 0 &= 0 && \\ 0 \BITAND 1 &= 0 && \\ 1 \BITAND 0 &= 0 && \\ 1 \BITAND 1 &= 1 && \REMTEXT{両方が$1$ のときだけ$1$} \\ \end{align*} $$
僕「確かにそうだね。 $0$ を偽に置き換えて、 $1$ を真に置き換えて、 $\BITAND$ を《かつ》に置き換えればぴったり同じだね。 書くのがたいへんだから、偽を《$F$》と書いて、真を《$T$》と書いて、《かつ》を《$\LAND$》にするよ」
論理積(かつ) $$ \begin{align*} F \LAND F &= F && \\ F \LAND T &= F && \\ T \LAND F &= F && \\ T \LAND T &= T && \REMTEXT{両方が$T$ のときだけ$T$} \\ \end{align*} $$
$F$ は偽、 $T$ は真、 $\LAND$ は《かつ》を表す。
ユーリ「同じ計算だ」
僕「そうだね。文字の置き換え、記号の置き換えをするだけで、 完全に入れ替わるってことは、同じ計算といえるよね」
ユーリ「『もしかして』」
僕「『わたしたち』」
ユーリ「『いれかわってる〜?』」
僕「時事ネタ自重!」
ユーリ「お兄ちゃんのノリツッコミ初めて見た」
僕「まじめに行こう」
ユーリ「あのね、 《変幻ピクセル》イベントで、 リサ姉が機械見せてくれたの(第103回参照)。 紙をスキャンして、 色が黒いところが $1$ になって、白いところが $0$ になるとき、 黒と黒が重なるときだけ黒をプリントする……みたいなの。 それが論理積」
僕「なるほどね。それは計算結果を図形の色に対応させてるんだ」
ユーリ「そんな感じ」
ユーリ「否定と、《かつ》と、それから《または》でしょ?」
僕「そうだね。命題を扱う命題論理だと、その $3$ つは大事だね。 《または》の真理値表はわかる?」
ユーリ「お兄ちゃんから聞いたことある。 少なくとも片方が真のときだけ、全体が真になるんでしょ?」
$P\REMTEXT{または}Q$の真理値表
$$ \begin{array}{|cc|c|} \hline P & Q & P \REMTEXT{または} Q \quad \\ \hline \REMTEXT{偽} & \REMTEXT{偽} & \REMTEXT{偽} \\ \REMTEXT{偽} & \REMTEXT{真} & \REMTEXT{真} \\ \REMTEXT{真} & \REMTEXT{偽} & \REMTEXT{真} \\ \REMTEXT{真} & \REMTEXT{真} & \REMTEXT{真} \\ \hline \end{array} $$
僕「そうだね」
ユーリ「ビット単位の論理和ってゆーのもあったよ!」
論理和(ビット単位) $$ \begin{align*} 0 \BITOR 0 &= 0 && \REMTEXT{両方が$0$ のときだけ$0$} \\ 0 \BITOR 1 &= 1 && \\ 1 \BITOR 0 &= 1 && \\ 1 \BITOR 1 &= 1 && \\ \end{align*} $$
僕「それに合わせて、 $F$ と $T$ で書いてみようか。《または》は $\LOR$ にして」
論理和(または) $$ \begin{align*} F \LOR F &= F && \REMTEXT{両方が$F$ のときだけ$F$} \\ F \LOR T &= T && \\ T \LOR F &= T && \\ T \LOR T &= T && \\ \end{align*} $$
ユーリ「こっちも、《$\BITOR$》と《$\LOR$》は同じ計算なんだね!」
僕「そうだね。同じ計算をやってるように見えるね」
ユーリ「あれ? もしかして……」
僕「もう時事ネタはいいよ」
ユーリ「違うの! そーじゃなくて、思いついたの!」
僕「何を?」
ユーリ「同じなの! 《かつ》と《または》って同じ計算じゃん!」
僕「?」
ユーリ「置き換えちゃう。 $F$ と $T$ を置き換えて、 $\LAND$ と $\LOR$ を置き換えるの!」
僕「書いてみようよ」
置き換えたらどうなる?
$$ \begin{array}{ccc} F & \RELATED & T \\ \LAND & \RELATED & \LOR \\ \end{array} $$
真理値表の置き換え
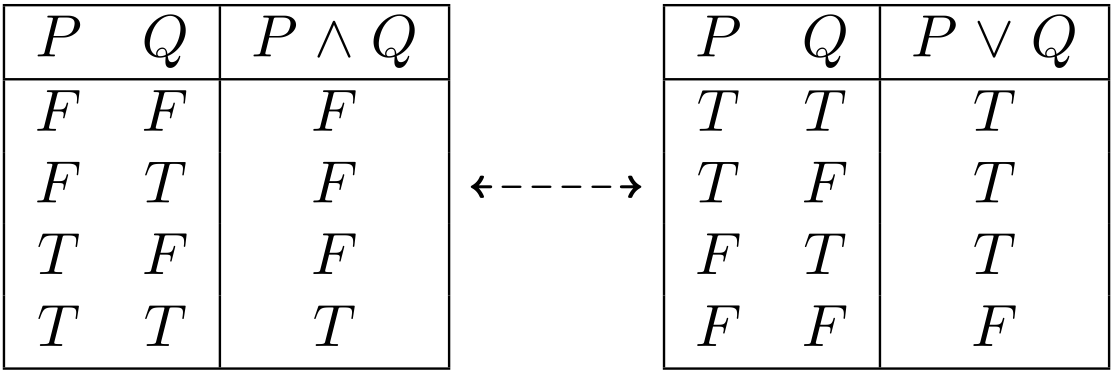
ユーリ「ね? ね? でしょでしょ? $F$ と $T$ を交換して、 $\LAND$ と $\LOR$ を交換しても、真理値表は正しいじゃん?」
僕「まったくその通り! すごいな!」
ユーリ「ねー、これって大発見?」
僕「そうだね! ユーリのこの発見は、 《ド・モルガンの法則》の言い換えになっているよ」
ユーリ「なにそれ」
僕「ド・モルガンの法則っていうのは、 論理の法則の一つだよ。 真偽を交換することと、論理和と論理積を交換することの関係を表してる」
ユーリ「へー」
僕「ド・モルガンの法則はいろんな書き方ができるけど、 たとえばこんなふうに書ける。 $\LNOT P$ というのは $P$ の否定のこと」
ド・モルガンの法則
命題 $P$ と命題 $Q$ の真偽に関わらず、 $$ P \LAND Q $$ と $$ \LNOT((\LNOT P) \LOR (\LNOT Q)) $$ の真偽はつねに一致する。
このことを
$$
P \LAND Q \equiv \LNOT((\LNOT P) \LOR (\LNOT Q))
$$
と書く。
$\equiv$ は《論理同値》を表す。
ユーリ「へ?」
僕「何が『へ?』なの? ユーリが発見したことと同じになってるよ」
ユーリ「お兄ちゃん得意の数式が出てきたけど、 これってユーリが言ったことと同じなの?」
僕「同じだよ。ユーリは $F$ と $T$ を交換して、 $\LAND$ と $\LOR$ を交換しても、 正しい真理値表ができるっていってたわけだろう?」
ユーリ「まーね」
僕「$F$ と $T$ を交換するということは、真偽を交換するわけだから、 否定 $\LNOT$ を使えばいいよね。 $P$ があったら $\LNOT P$ にして、 $Q$ があったら $\LNOT Q$ にする。 最後に全体の式もまとめて否定 $\LNOT$ する」
ユーリ「そっか……」
僕「そういうつもりでもう一度式を読んでごらんよ」
ユーリ「じー」
$$ P \LAND Q \equiv \LNOT((\LNOT P) \LOR (\LNOT Q)) $$僕「ね?」
ユーリ「なーるほど! わかった。ほんとだ。 左辺の $P$ を $\LNOT P$ で置き換えて、 $Q$ を $\LNOT Q$ で置き換えて、 $\LAND$ を $\LOR$ で置き換えて、全体に $\LNOT$ 付けたのが右辺になってる」

僕「そうそう。それで正しく式を読んでいるよ。 左辺 $P \LAND Q$ の真理値表と、 右辺 $\LNOT((\LNOT P) \LOR (\LNOT Q))$ の真理値表を比べてみれば、 そうすると、この $2$ つの真理値表が一致することがわかるよ」
$P \LAND Q$ の真理値表
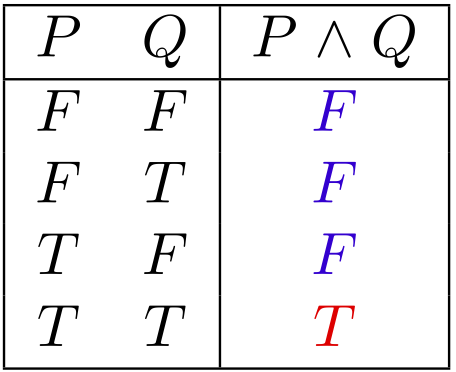
$\LNOT((\LNOT P) \LOR (\LNOT Q))$ の真理値表
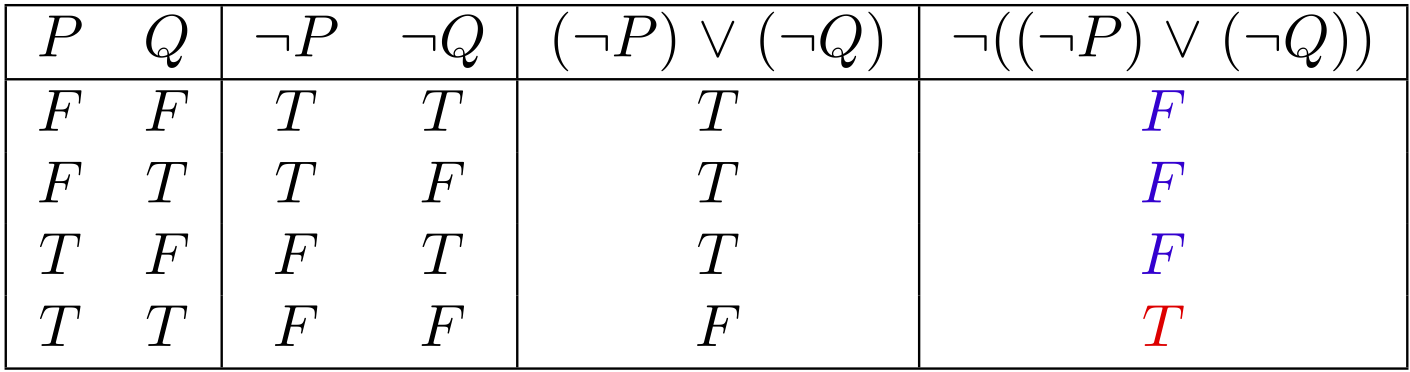
ユーリ「……両方とも、 $F F F T$ ?」
僕「そうだね。ということは、 $P,Q$ の真偽に関わらず、 この $2$ つの式の真偽は一致するといえる。 $P \LAND Q$ が $T$ のとき、 $\LNOT((\LNOT P) \LOR (\LNOT Q))$ も $T$ になるし、 片方が $F$ なら、他方も $F$」
ユーリ「……」
僕「ド・モルガンの法則はもう一つあるよ。 もう一度 $\LAND$ と $\LOR$ を置き換えたものだね。 まとめて書いておこうか」
ド・モルガンの法則
$$ \begin{align*} P \LAND Q &\equiv \LNOT((\LNOT P) \LOR (\LNOT Q)) \\ P \LOR Q &\equiv \LNOT((\LNOT P) \LAND (\LNOT Q)) \\ \end{align*} $$
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2016年10月14日)