第171回 シーズン18 エピソード1

裏の裏は表（前編） ただいま無料

僕の部屋

ユーリ「ねーお兄ちゃん。退屈なんだけど」

僕「もう、本は読み終わったの？」

ユーリ「本は飽きちゃった。ねー、退屈退屈！」

僕「ユーリは退屈であることを表明している」

ユーリ「なにそれ」

僕「いや、客観的事実を文章で描写することによる状況分析」

ユーリ「……それ、楽しい？」

僕「特に楽しくはないけど」

ユーリ「どっと疲れた。何かおもしろい話ないの？」

僕「ユーリはおもしろい話を求めている」

ユーリ「ねー、ちょっと叩いてもいい？」

僕「わかった、わかったよ。そうだなあ……ユーリは、 こんなクイズを知ってるかなあ」

ユーリ「なになに？」

僕「クイズの意味はわかるよね？　カードが……」

ユーリ「わかるわかる！　カードがあって、猫とか犬とか書いてあって、 めくると整数が書いてあるんでしょ？　で、猫の裏側は奇数か？」

僕「そうそう。ざっくり言うとそうだね」

ユーリ「猫の裏側が奇数かどうかを確かめるんだから、 奇数の［ $13$ ］と［猫］をめくればいーんじゃないの？」

僕「そう思うよね。でも……」

ユーリ「待った！　待って待って！　お兄ちゃんが《そう思うよね》 と言ったときはヤバい」

僕「ヤバいとは？」

ユーリ「何か《引っ掛け》が混じってるってこと！　も少し考える！」

僕「はいはい」

ユーリ「……このクイズ、おもしろいね」

僕「そう？」

ユーリ「ユーリわかったよ！　あのね、 めくらなくちゃいけないのは、［猫］と［ $40$ ］でしょ？」

僕「はい、正解です」

ユーリ「やたっ！」

僕「そのようすだと、理由もちゃんとわかっているみたいだね」

ユーリ「わかってるよん。 ［猫］の裏側が奇数なんだから、［猫］はめくる必要あるじゃん。 でも［ $13$ ］はもともと奇数だからどーでもよくて、 偶数の［ $40$ ］はチェックがいる。［犬］はどーでもいい」

僕「うん、わかっている人が聞いたら、 その答え方でユーリがわかっていることはわかるだろうね」

ユーリ「なにその言い方」

僕「順序立てて確かめてみようか。［ $13$ ］をめくらなくてもいい理由は？」

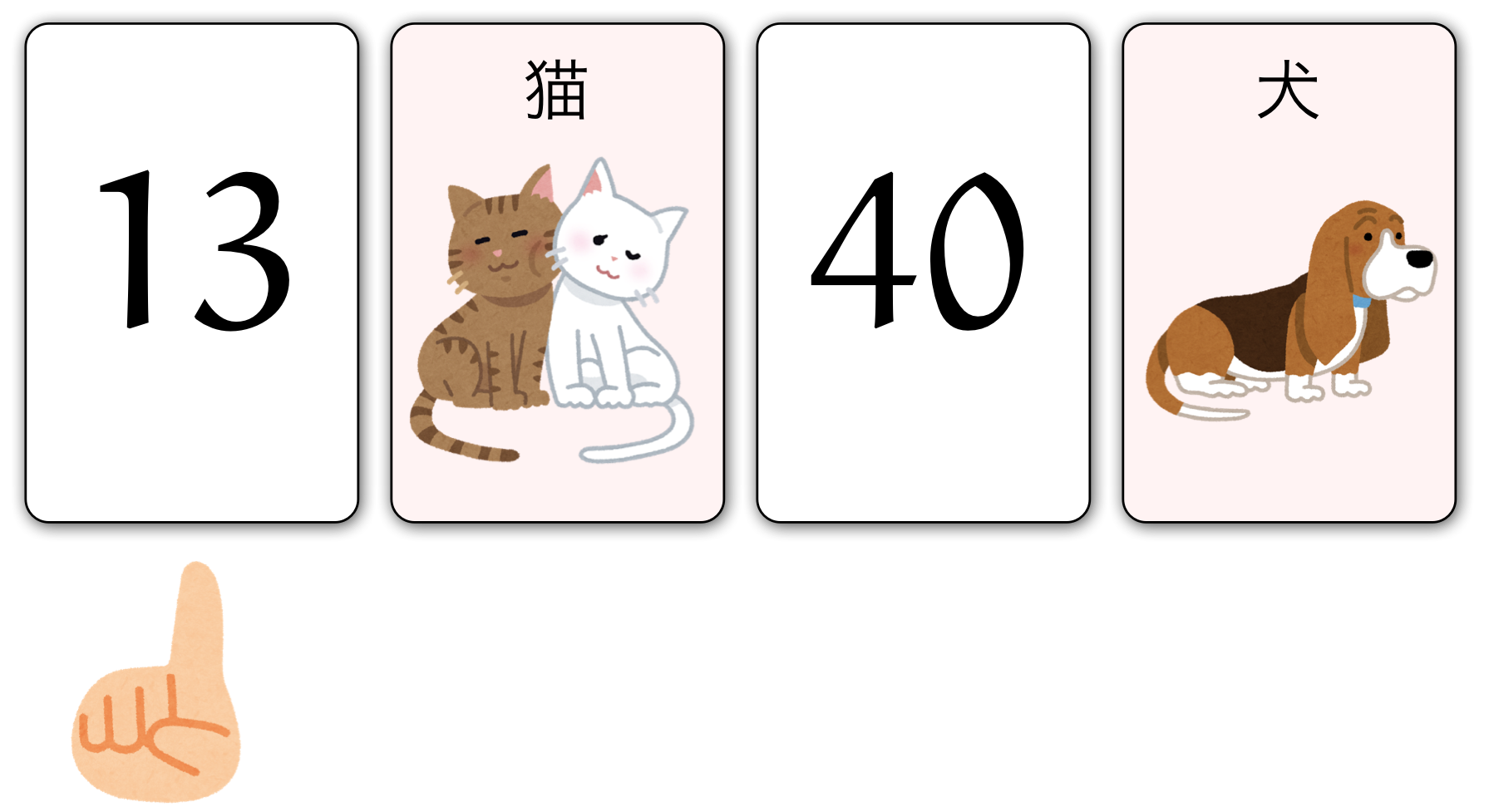
ユーリ「奇数はどーでもいいから！」

僕「どうでもいいというのは？」

ユーリ「えーとね、いま知りたいのは［猫］の裏側が奇数かどうかでしょ？」

僕「そうだね」

ユーリ「［猫］の裏側が奇数かどうかを知りたい。 もしも、奇数である［ $13$ ］の裏側が［猫］だったら、 それで問題ないでしょ？」

僕「問題ないね。［猫］の裏側は奇数であるというルールは破られない」

ユーリ「でも、もしも［ $13$ ］の裏側が［犬］でも［ライオン］でも、 そんなのは［猫］とは関係ないじゃん？」

僕「そうそう。［ $13$ ］の裏側が［猫］以外だったら、 ［猫］の裏側は奇数であるというルールはやっぱり破られない」

ユーリ「だから結局、［ $13$ ］の裏側が何であるかなんて、 確かめる必要はぜーんぜんない。影響ないもん」

僕「その通り！　じゃ、次のカード。 ［猫］をめくる必要があるのはなぜ？」

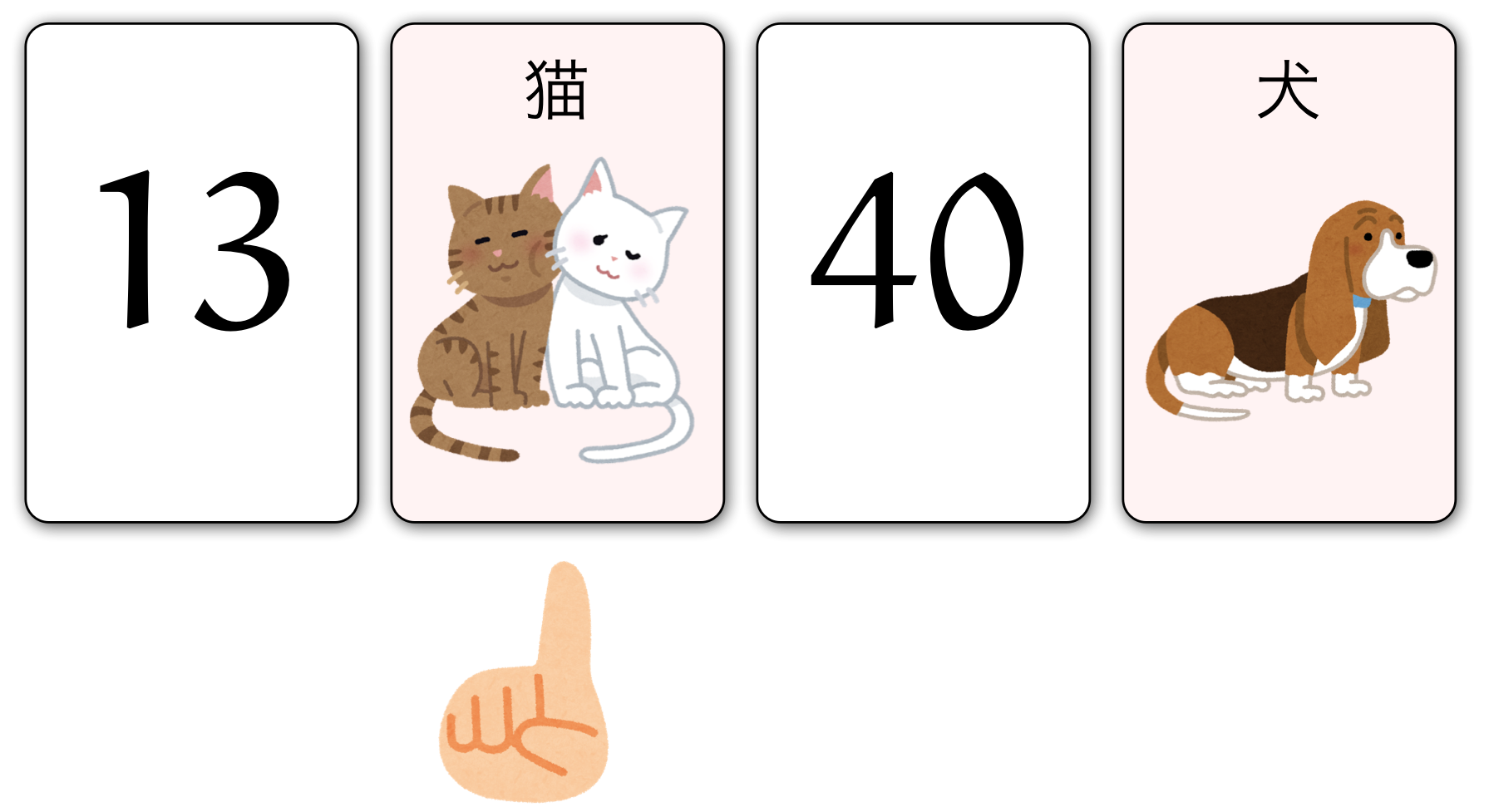
ユーリ「これはめくる必要あるよー。あったりまえじゃん。 だって［猫］の裏側が奇数だったらいーけど、 偶数だったらアウト！だもん」

僕「そうなるね。［猫］の裏側は奇数であるというルールは、 ［猫］の裏側が偶数だったら破られた。 でも［猫］の裏側が奇数だったら破られない。 だから、めくって確かめる必要がある」

ユーリ「そだね」

僕「じゃあ、その次のカード。［ $40$ ］をめくる必要があるのはなぜ？」

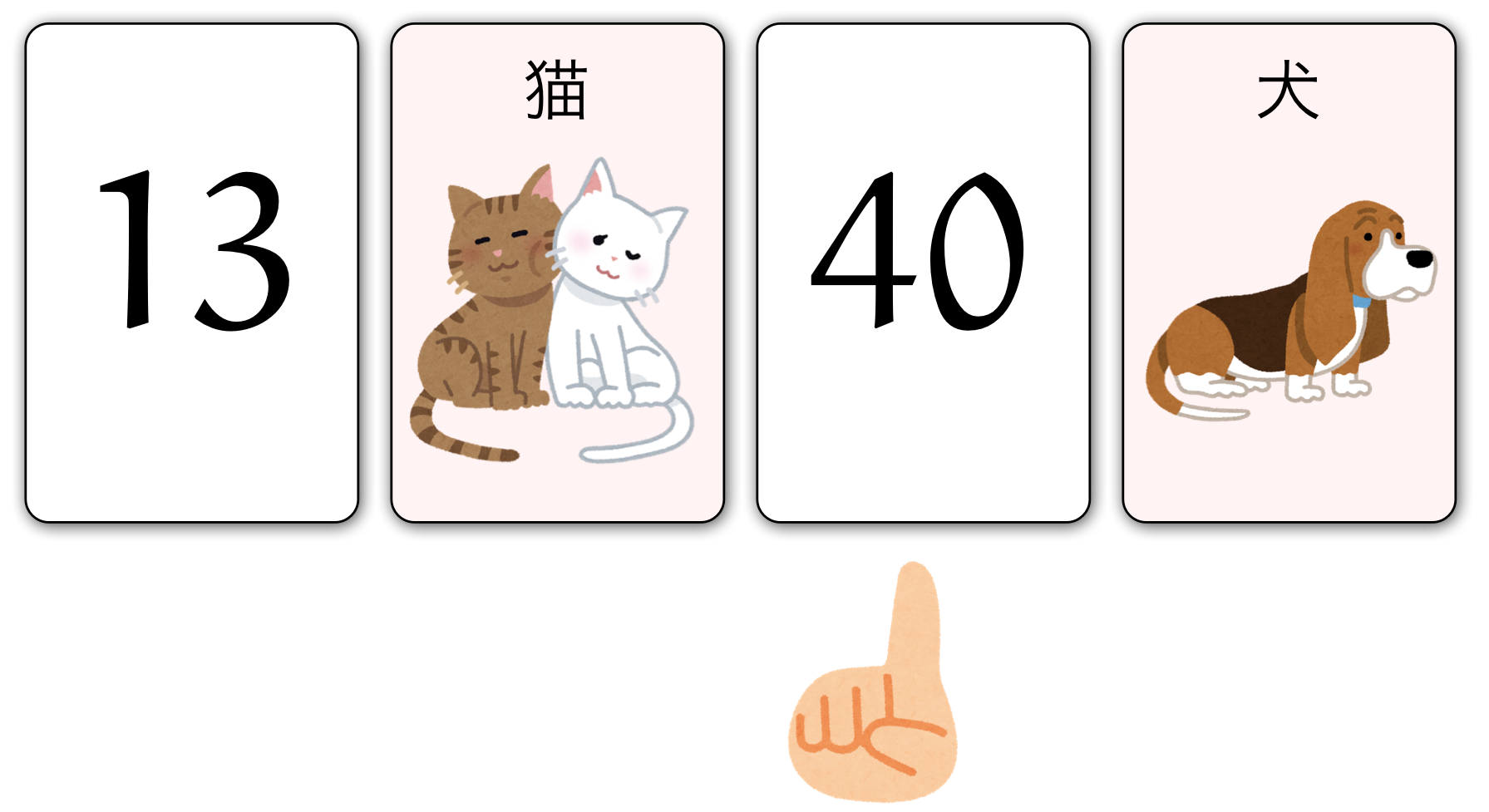
ユーリ「これ！これがおもしろかった！だって、 ［ $40$ ］って偶数だから、めくって［猫］ならアウトだもん！」

僕「そうだね。［猫］の裏側は奇数であるというルールは、 偶数である［ $40$ ］の裏側がもしも［猫］だったら破られる。 だって、［ $40$ ］の裏側が［猫］になってるカードは、 ［猫］の裏側が偶数になってるカードってことだからね」

ユーリ「［ $40$ ］をめくって［イルカ］だったらセーフ」

僕「なぜにイルカ？　でも、その通り。［ $40$ ］をめくって、 ［猫］以外が出れば問題はない。だって、そのカードは、 ［猫］の裏側が奇数というルールとは無関係だから」

ユーリ「最後のカードの［犬］も無関係だから、めくらなくていい」

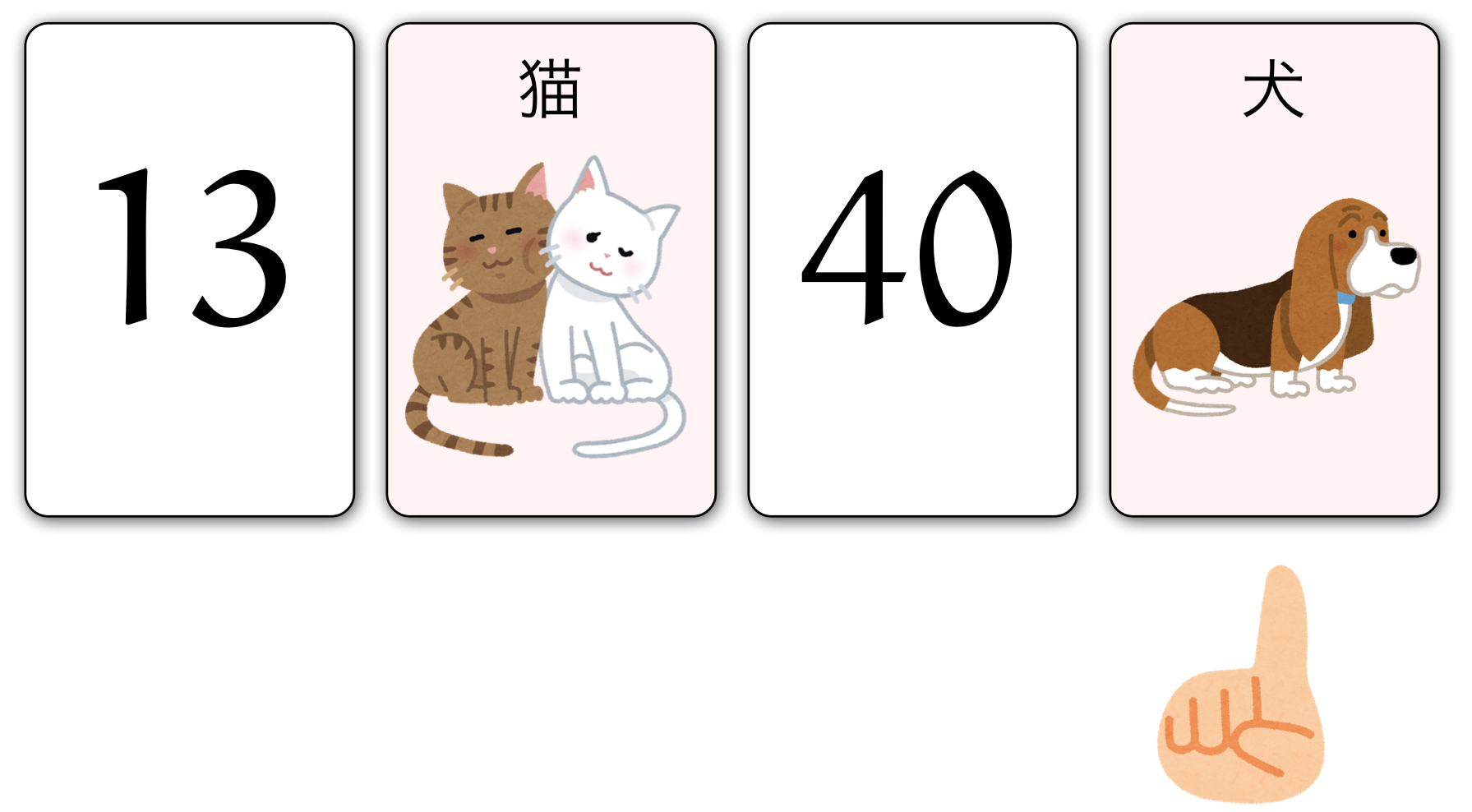
僕「その通り。［猫］の裏側は奇数であるという主張を確かめるのに、 ［犬］のカードは関係がない。［犬］の裏側が偶数でも奇数でも、 主張に影響しないからね」

ユーリ「あのね、ユーリがおもしろい！って思ったのは、 ［ $40$ ］のカードなの。これって偶数なのにめくる必要があるじゃん？ 《［猫］の裏側は奇数である》の中に偶数は出てこない。 だから偶数のカードは無関係かと思わせといて、 実はそれをめくる必要があるの。それがおもしろかった！」

僕「いいね！　お兄ちゃんもそう思うよ。 でもね、いまユーリは《［猫］の裏側は奇数である》の中に偶数は出てこないから、 偶数のカードは無関係って言ったけど、 論理的にいえば、無関係じゃないよね」

ユーリ「へ？」

僕「だって、整数は偶数か奇数かのどちらかなんだから、 《奇数である》は《偶数ではない》と言い換えられる。 だから無関係じゃないんだ」

ユーリ「あー……ま、そだね」

僕「論理的な話をするとき、的確に言い換えるのは大事なんだよ。 たとえば、《［猫］の裏側は奇数である》は、 《［猫］の裏側は偶数ではない》と言い換えても問題がおきないよね？」

ユーリ「おおー、確かに！　そっか……《［猫］の裏側は偶数ではない》 を確かめるって考えると、 偶数の［ $40$ ］をめくるのはそんなにおかしくないね」

僕「でも……よく考えてみると、確かにこのクイズはおもしろいな」

ユーリ「なにいまさら」

僕「いや、お兄ちゃんはこのクイズ、何かの本で見かけたんだけど、 そのときはあまり気にしてなかったんだ。 でも改めてユーリに出題してみると、このクイズのおもしろさがわかったような気がする」

ユーリ「そなの？」

僕「たとえばね、この二つのルールって、同じことをいってると思う？」

• （Ａ）［猫］の裏側は、偶数である。
• （Ｂ）偶数の裏側は、［猫］である。

ユーリ「えーと？　うん。同じこと……んにゃっ！　違うにゃっ！」

僕「ユーリは猫にならなくていいから。 この（Ａ）と（Ｂ）は違うこといってるよね。 ［猫と $40$ ］［犬と $40$ ］［イルカと $13$ ］という三枚のカードがあったとしたら、 ルール（Ａ）は正しいけれど、ルール（Ｂ）はまちがっている。 だって、偶数の［ $40$ ］の裏側が［犬］になっているカードがあるから」

ユーリ「そーだね！　順番が入れ替わっただけなのに、 意味がちがっちゃうんだ！」

僕「じゃあね、今度はこの二つのルールって同じことをいってると思う？」

• （Ｃ）［猫］の裏側は、偶数である。
• （Ｄ）奇数の裏側は、［猫］ではない。

ユーリ「うー……たぶん。たぶん、同じこといってると思う」

僕「同じこといってるって断言はできない？」

ユーリ「……断言できる。できる！　だってね、 ［猫］の裏側が必ず偶数だとしたら、奇数の裏側が［猫］になるはずないもん！」

僕「おお。そうだね。そして……」

ユーリ「そして、［猫］の裏側が偶数でないカードがあるとしたら、 そのとき、奇数の裏側が［猫］になってるカードがあるってことだから！」

僕「すごいすごい」

ユーリ「へへ……これって、お兄ちゃん教えてくれたことあるよね」

僕「そうだね。よく覚えてたね。論理の話だ」

ユーリ「もう忘れちゃったけど」

僕「がく」

ユーリ「ややこしーんだもん」

僕「いやいや、論理っていうのはもともと《ややこしいものを解きほぐして、 整理して、まちがいがないように考える》ためのものだよ。 ひとつひとつはあたりまえのように見えることだけど、 それを積み重ねていくと、うっかりミスを防いだり、 誤解しないようにできる。数学の問題を考えるときも、 論理を使っていることを意識した方がいい」

ユーリ「おー！　《先生トーク》……」

命題と真偽

僕「さっきは $40$ が偶数だとか、言ってたよね。 《$40$ は偶数である》というのは正しいし、 《$13$ は偶数である》というのは正しくない」

ユーリ「うん」

僕「そんなふうに、正しいか正しくないか判断できる主張のことを命題（めいだい）っていうんだ」

ユーリ「めーだい」

僕「だから《$40$ は偶数である》というのは命題だし、 《$13$ は偶数である》というのも命題になる」

ユーリ「《$13$ は偶数である》ってゆーのはまちがいだけど、 それでも命題なの？」

僕「そうだよ。正しくない命題だね。 正しい命題のことは論理では真（しん）の命題といって、 正しくない命題のことは偽（ぎ）の命題というんだ」

• 《$40$ は偶数である》　真の命題
• 《$13$ は偶数である》　偽の命題

ユーリ「ふんふん」

僕「それではここでクイズです。命題ではないものの例を挙げよ」

ユーリ「え……だって、《$13$ は偶数である》も命題なんでしょ？ 真でも偽でも命題は命題じゃないの？」

僕「そうだね。 だから真であるとも偽であるともいえないものを考えればいいんだよ。 たとえば、《$13$》という整数は命題じゃない。 真であるとも偽であるともいえないからね」

ユーリ「ははーん。にゃるほど。だったら《$40$》も命題じゃない」

僕「そういうことだね。《にゃるほど》というのも命題じゃない」

ユーリ「真であるとも偽であるともいえないから？」

僕「その通り！　《早く宿題しなさい！》も命題じゃない」

ユーリ「命題じゃなくて命令」

僕「オチを付けなくてもいいよ……じゃあね、 《$1+2 = 3$》というのは命題だと思う？」

ユーリ「《$1+2 = 3$》は正しい……真だといえる……命題？」

僕「そうだね。《$1+2 = 3$》は命題になる。でも《$1+2$》は命題じゃない」

ユーリ「そりゃそーだ」

否定

僕「何か命題があったとき、そこから別の命題を作ることもできるよ。 よく使うのが否定（ひてい）だね」

ユーリ「ひてー」

僕「《$13$ は奇数である》という命題の否定は、 《$13$ は奇数ではない》という命題になる」

ユーリ「ふんふん。あれ？　《$13$ は奇数ではない》ってゆーのは偽だよ？」

僕「そうだね。ある命題を否定して作った別の命題は、 真と偽が逆転することになるね。 真の命題を否定したら偽の命題になって、 偽の命題を否定したら真の命題になる」

ユーリ「それって、あたりまえのこと言ってるよね？」

僕「そうだね。話としてはあたりまえだと思うよ。 でも大事なのは、僕たちがふだん使っている言葉の働きを、 ひとつひとつ論理の世界にうつそうとしている点なんだよ」

ユーリ「なにいってるかわかんない」

僕「ほら、僕たちが考えるときっていうのは、 必ずしも《正しい》《正しくない》だけで考えているわけじゃないよね。 こうかなあ、ちがうかなあ、やっぱりそうだ！というふうに」

ユーリ「そだね。おなかへったなあ、とか」

僕「あはは。でもとりあえずはそういうのはわきに置いといて、 論理的に考えを進めるための要素というか部品のようなものを、 ひとつひとつ集めてみようとしてるんだ。 論理的に考えるためには、あいまいにならないようにしたい。 だから、まずは真か偽か判断できるものだけを取り扱おうとしてみよう」

ユーリ「ほほー？」

僕「ということで命題というものを考える。 そうすると、何の心配もなく《真の命題》や《偽の命題》の話ができることになる。 だって、命題は真か偽かどちらかになるものだから」

ユーリ「ふんふん！　バシッと決まるものだけを使うってことだね！」

僕「そうだね。 そして、ある命題を否定した命題というものも考えることができる。 《真の命題》を否定すると《偽の命題》になるし、 《偽の命題》を否定すると《真の命題》になる。 それは、僕たちが、確かにそれはあたりまえだよね、 といえる部品をもってきたことになるんだ。否定という部品だね」

ユーリ「難しーけど、何となくわかった。でもね、お兄ちゃん。 そんなふうに《あたりまえ》のものだけ集めてたら、 結局《あたりまえ》のことしか考えられないんちゃいますのん？」

僕「あやしい関西弁やめい。 ユーリが言いたいことはわかるよ。でも、そうじゃない。 《あたりまえ》っていうのは、そんなことわざわざ主張しなくても、 わかりきっているって意味だよね。いうまでもないとか」

ユーリ「そだね」

僕「でも、一歩一歩はあたりまえでも、 それをたくさんたくさん積み重ねて、 最初と最後を見たときにはちっとも《あたりまえ》じゃなくなる。 スタートからゴールまではものすごい距離が離れることになるから」

ユーリ「そーゆーもん？」

僕「そういうもの」

かつ

ユーリ「まーいーや、話を先に進めたまえ」

僕「偉そうだな。さっきは《否定》の話をしてたんだった。 次は《かつ》の話をしよう。 《かつ》を使うと、二つの命題 $P$ と $Q$ を組み合わせて、 新しい命題を作ることができる」

• 命題 $P$《$40$ は偶数である》
• 命題 $Q$《$13$ は奇数である》

僕「ここで、《$P \REMTEXT{かつ} Q$》は新しい命題になるんだ」

ユーリ「《かつ》って知ってる。お兄ちゃんよく使うし。 で、次は何？　《または》だっけ？」

僕「いやいや、そんなに先を急がないでほしいな、ユーリ。 『$P \REMTEXT{かつ} Q$は命題である』って聞いたら、 何を考えるべきだと思う？」

ユーリ「何を……考えるべきかって？」

僕「そう」

ユーリ「何を……って、わかんにゃい。 $P \REMTEXT{かつ} Q$って、$P$と$Q$が両方のときでしょ？」

僕「$P$ と $Q$ が両方、何のときに何なの？」

ユーリ「何を聞かれてるかわかんない……」

僕「『$P \REMTEXT{かつ} Q$は命題である』と言われたとき、 すぐに考えるべきことは、こういうことだよ」

• 命題というのは真か偽かどちらかである。
• $P$ は命題だから、真か偽かどちらかである。
• $Q$ は命題だから、真か偽かどちらかである。
• $P \REMTEXT{かつ} Q$も命題なんだから、真か偽かどちらかである。

ユーリ「だから！　さっきから言ってるじゃん！　$P$と$Q$が両方とも真のときに、$P \REMTEXT{かつ} Q$は真になるんでしょ？」

僕「そうだね！　その通り。 $P$ と $Q$ の両方が真のとき、 そしてそのときだけ、$P \REMTEXT{かつ} Q$は真になる。 そのように、$\REMTEXT{かつ}$というものを定めることにしよう」

ユーリ「むー……」

僕「何むくれてるの？」

ユーリ「むくれてなんかいないもん！　ユーリがさっきから言ってること、 お兄ちゃんは無視して話を進めるじゃん？　それおかしくない？」

僕「そんなことないよ。お兄ちゃんはユーリが言ってること、 ものすごくしっかり聞いてるんだよ。ユーリが命題のことを話すとき、 《真》や《偽》という表現を使うかどうか、そこに耳をすませてる」

ユーリ「むー……そーゆーこと？　でも、ユーリわかってるもん。 《かつ》なんてしょっちゅう使ってるし！」

僕「そうだね。ユーリはよくわかっているよ。わかってなければ、 あんなふうにいえない。そういえば、こんな会話、以前もやったよね」

ユーリ「？」

僕「数式でアピールする話だよ（『数学ガールの秘密ノート／式とグラフ』参照）。 日本語も言葉。数式も言葉。 どちらも、自分の考えを相手に伝えるためにある。 自分が一生懸命考えたことを、 しっかりとまちがいなく相手に伝えるためにある」

ユーリ「……」

僕「だから、どんな言葉を使うかは大切にしないとね」

ユーリ「……大切にしてるつもりなんですけど！」

僕「そうだね、ユーリはえらいよ」

真理値表

僕「命題は真か偽か判断できる。真の命題と偽の命題という二通りがある。 でも、命題が多くなってくると、真と偽の組み合わせはどんどん増える。 それを整理するために真理値表（しんりちひょう）というものがある」

ユーリ「しんりちひょう」

僕「命題 $P$ は真か偽の二通りのどちらか。そのそれぞれに対して、 命題 $Q$ は真か偽の二通りのどちらか。だから組み合わせは全部で何通り？」

ユーリ「$4$ 通り」

僕「そうだね。 $2 \times 2 = 4$ 通りある。 それをこんなふうにまとめたものが真理値表」

ユーリ「ふんふん。これ、見たことある」

僕「まあ、よく書くからね」

ユーリ「……これって、命題 $P$ が真で、命題 $Q$ が真のときに限って、 $P \REMTEXT{かつ} Q$が真になるっていってるんでしょ？」

僕「そうだよ」

ユーリ「これって《計算》してるみたい」

僕「そうだね！　その通り。その考えで合ってるよ。 真と偽という二つの値を使って、 《かつ》という計算をしていると考えることができる。 《真かつ真》のときだけ計算結果が真になるという計算だね」

ユーリ「んー、だったら、真理値表って、こー書いてもいいね！」

僕「いいねえ！」

ユーリ「ね！　九九の表みたい！　……あ、思い出した。ほら、リサ姉（ねー）のこと」

僕「リサちゃん？」