第154回 シーズン16 エピソード4

-4を作ろう（後編）

ユーリ「順序対（じゅんじょつい）というものを使えば、整数が作れる……でも、待ってお兄ちゃん！ うっかりナットクしてしまいそーになりましたぜ」

僕「……」

ユーリ「お兄ちゃんは、 $(m, 0)$ を $m$ だと見なして、 $(0, n)$ を $-n$ と見なしてるわけだよね？」

ユーリ「確かにこれだと、 $2$ と $3$ を足せば $5$ になるし、 $-2$ と $-3$ を足せば $-5$ になるけど……」

僕「……」

ユーリ「でもね、 $3$ と $-3$ を足しても、 $0$ にならないじゃん！　 $(3,0)$ と $(0,3)$ はどーやって足すの？　 $(0,0)$ にしなくちゃ！」

僕「そうだね。ユーリのいう通りだよ。 僕たちがここまで考えてきたのはこういうことだったよね」

• 集合を使って $0,1,2,3,\ldots$ という数を作った。
• $(m,0)$ や $(0,n)$ という順序対を作って、それを整数に対応付けた。
• 《$0$ および負の数同士の足し算》《$0$ および正の数同士の足し算》を作ってきた。

ユーリ「うん」

僕「でも、ユーリのいう通り、負の数と正の数の《足し算》は定義していないね。 まだ」

ユーリ「$(3,0)$ を $3$ だと思って、 $(0,3)$ を $-3$ だと思うんだから、 $$ (3,0) + (0,3) = (0,0) \qquad \REMTEXT{（？）} $$ になってほしい！」

僕「うん、ミルカさんから教えてもらったのは、 $(m,n)$ という順序対はまるでベクトルみたいだ、ということなんだよ」

ユーリ「ベクトル？　ここでベクトルが出てくるの？」

僕「そうだね。でも、ベクトルのことは気にしなくていいよ。 ともかく、いまは $(a,b)$ と $(c,d)$ の足し算、 つまり《順序対の和》を次のように定義してみる」

ユーリ「なんか、急にややこしくなった」

僕「そんなことないよ。正の数同士、負の数同士の足し算をちょっと拡張しただけだよね。次の三つの式をよく見比べればわかるよ」

$$ \begin{align*} (a,b) + (c,d) &= (a+c,b+d) && \REMTEXT{順序対の和} \\ (m,0) + (n,0) &= (m+n,0) && \REMTEXT{$0$および正の数同士の和} \\ (0,m) + (0,n) &= (0,m+n) && \REMTEXT{$0$および負の数同士の和} \\ \end{align*} $$

ユーリ「……あ、まー、そーだね。 お兄ちゃんが言いたいのは、こーゆーことでしょ？」

$$ \begin{align*} (a,b) + (c,d) &= (a+c,b+d) && \REMTEXT{順序対の和} \\ (a,0) + (c,0) &= (a+c,0+0) && \REMTEXT{$b = 0, d = 0$の場合} \\ (0,b) + (0,d) &= (0+0,b+d) && \REMTEXT{$a = 0, c = 0$の場合} \\ \end{align*} $$

僕「そうそう、そういうこと。《順序対の和》で、 $b = 0, d = 0$ や $a = 0, c = 0$ とすれば、 《$0$ および正の数同士の和》にも《$0$ および負の数同士の和》にもなる」

ユーリ「にゃるほど。はい、おめでとーございます。 これで整数全体の足し算ができましたねー……なんていかないよ！　だって、やっぱり、 $$ (3,0) + (0,3) = (3+0,0+3) = (3,3) $$ だから、だめだもん！ $(0,0)$ にならなきゃいけないのに！」

僕「そうだね。 $3$ と $-3$ を足したら $0$ になってほしい。 だから、 《$3$ を表している順序対の $(3,0)$》と 《$-3$ を表している順序対の $(0,3)$》を足したら、 《$0$ を表す順序対である $(0,0)$》 になってほしい。ユーリの気持ちはまったく正しいよ」

ユーリ「ふむー……そんで？　どーすんの？」

僕「そこで、こう考えてみる。 《順序対の和》はさっきの定義のままにしておいて、 その上で、 $(3,3)$ と $(0,0)$ は実は仲間だと見なす。 つまり、 $(0,0)$ だけじゃなくて、仲間である $(3,3)$ も、 $0$ を表している順序対だ！……ということにする」

ユーリ「なにその、いきあたりばったりな考え方。 数学とは思えない。テキトーな……んにゃ、それでもダメだよ、お兄ちゃん！　 いまユーリは $(3,0)+(0,3)$ の話をしたけど、 $(1,0)+(0,1)$ はどーすんの？ $1$ と $-1$ を足したら、 これも $0$ になってほしーよ？　でも $(1,0)+(0,1)=(1,1)$ になっちゃうじゃん！」

僕「そうそう。だから、 $(1,1)$ も $(0,0)$ の仲間であって、 $0$ を表している順序対だと見なそう！」

ユーリ「だって……だって……そんなことしたら、 たくさんルールがいるじゃん。アレとコレは同じと見なす、 アレもコレもなんて、そんなの数学じゃないよー、やめてよー」

僕「そうでもないんだよ、ユーリ。いまは順番に考えてきたから、 例として、 $(3,3)$ も $(1,1)$ も $(0,0)$ だと見なすという話になっちゃったけど、 いきあたりばったりに考えているわけじゃない。 $$ (m,m) $$ という形の順序対だけを $(0,0)$ の仲間にしようというんだ。 $(a,b)$ という順序対のうち、 $a = b$ を満たすものだけを集めて、 その全体で整数 $0$ を表すものだと見なそうということ」

ユーリ「……？」

僕「《$(m,m)$ という順序対全体の集合》を《整数 $0$》と呼ぼう！」

ユーリ「……！」

僕「整数 $0$ と同じようにして、整数 $1$ を作ってみる。 順序対 $(1,0)$ だけを $1$ と見なしてしまうと、 ユーリが気にしているようなことがまた起きる。 たとえば、 $(2,0)$ と $(0,1)$ という二つの順序対の和は、 $$ (2+0,0+1) = (2,1) $$ になるけど、 これって整数 $2$ と整数 $-1$ の和である整数 $1$ になってほしい。 だったら、 $(2,1)$ は $(1,0)$ の仲間にしてあげたくなる。 そこでね、こんな順序対の集合を作って、それを改めて整数 $1$ と呼ぼう！」

ユーリ「うー……」

僕「いま作った整数 $1$ は、 $$ (m+1, m) $$ という形の順序対すべてからなる集合だよ」

ユーリ「そっか……仲間をぜんぶいれちゃう？」

僕「もしも《整数 $-1$》を作りたかったら、どうする？」

ユーリ「……順序対 $(m,m+1)$ を仲間にしちゃう？」

僕「そうだね！ $(m,m+1)$ という形の順序対をぜんぶ集めて集合にする」

ユーリ「集めて……集合に」

僕「これで僕たちは、《順序対の集合》を使って、 《整数》を作れたことになる」

ユーリ「……」

僕「空集合から始まって、 僕たちは《ノイマンの方法》で $0,1,2,3,\ldots$ を作ってきたよね。 このときの $0$ は、 $$ \{\} $$ という集合に付けた名前だった。集合に名前を付けた」

ユーリ「うん……それはわかってる」

僕「それと同じように集合に名前を付けてるんだよ。 僕たちはいま、順序対の集合を使って整数を作ろうとしている。 このときの整数 $0$ は、 $$ \{(0,0),(1,1),(2,2),(3,3),\ldots\} $$ という順序対の集合に付けた名前ということになる。 これはかなり頭を柔らかくしないと納得できないと思うけど……」

ユーリ「うー……ちょっと聞きたいことあんだけど」

僕「何？　なんでもいいよ」

ユーリ「ごちゃごちゃしてわかんなくなった。 《ノイマンの方法》で作った $0$ と、 いまの整数 $0$ は《違うもの》だよね？」

僕「ああ、そうだね。違う違う。確かに違うよ。 何回も名前を付け直しているから混乱するかもね」

ユーリ「うん……すごく混乱してた。 《ノイマンの方法》で $3$ を作るときは、 $$ \{ 0, 1, 2 \} $$ を $3$ って呼ぶことにしたけど、 このときの $0$ は《ノイマンの方法》の $0$ だよね？」

僕「そうだね。その通り。このときの $0$ は、集合の言葉で書けば $\{\}$ ということになる」

ユーリ「それで、いまは《整数》を作ろうとしていて。そこでは、 $$ \{(0,0),(1,1),(2,2),(3,3),\ldots\} $$ を整数 $0$ と呼ぶことにする？」

僕「うん、そうだね。だから、ほんとうは整数 $0$ のことは $[0]$ のように別の記号を使った方がわかりやすいかもしれないね。 こんなふうに」

ユーリ「ほー……」

僕「並べてみようか」

ユーリ「それはそれでごちゃごちゃするよーな……ま、その名前の話はいーや。 整数の足し算はどーなったんだっけ、結局」

僕「ユーリが気にしていた《$3$ と $-3$ の和が $0$ になってほしい》というのは、 だから、 $$ [3] + [-3] = [0] $$ が成り立つようにしたいということなんだね」

ユーリ「えーと……これは、集合の言葉でいうと、

ということ……」

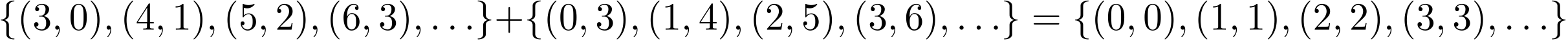
僕「そうだね。このような等式が成り立つように、 《順序対の集合》の和を定義すればいいということ。つまり、

に出てくる $+$ という記号を定めましょうと。 さっきユーリは、この集合の要素の中の一つずつ、つまり順序対 $(3,0)$ と順序対 $(0,3)$ を足してみて、 $(0,0)$ にならない！　と苦情をいってたんだね」

ユーリ「だって、順序対の和だったら、 $(3,3)$ になるんだもん、しょうがないじゃん！」

僕「確かに $(3,3)$ になってしまう。でも、ほら、よく見ると、 $(3,3)$ は $[0]$ の要素ではあるよね？　つまり、 $(0,0)$ の仲間にはなってる」

$$ [0] = \{(0,0),(1,1),(2,2),\underline{(3,3)},\ldots\} $$

ユーリ「そんなの、たまたまでしょ。てか、 $(3,3)$ が $(0,0)$ を仲間にしたのはそのためだもん」

僕「よくこの式を見てごらんよ」

ユーリ「じー」

僕「よく見るとわかるけど、 $[3]$ という集合から順序対を一つ持ってきて、 $[-3]$ という集合から順序対を一つ持ってきて、 その二つの順序対を足す。 そうすると、その結果となった順序対は、 $[0]$ という集合の要素になっているんだよ。 順序対をどのように選んでも、そうなる」

ユーリ「え？　どれを選んでも？　ほんとに？」

僕「確かめてみればいい。さっきは $(3,0)$ と $(0,3)$ だけを調べたけど……」

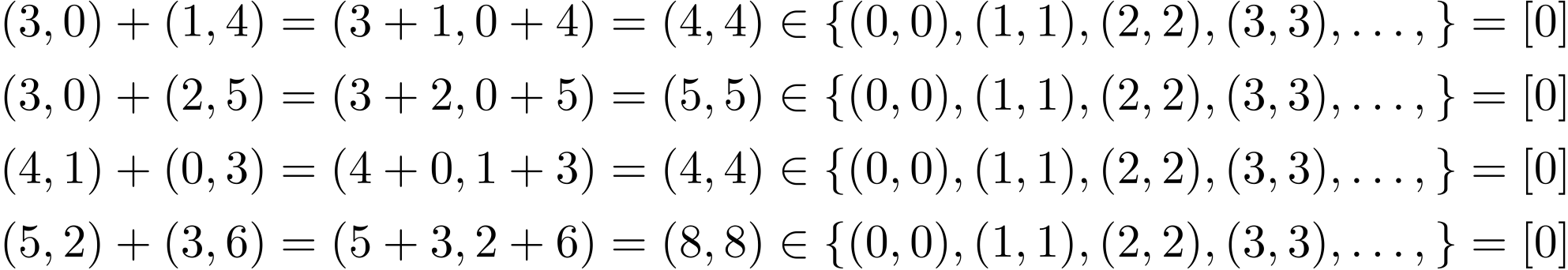
ユーリ「へーっ！　おもしろい！　お兄ちゃん、これおもしろいよ。 なんでそんなにうまくいくの？　 $[3]$ から好きなの選んで、 $[-3]$ から好きなの選んで、 両方足したら絶対に $[0]$ の中に入ってるんだ！」

僕「そうだよ。 だってね、 $[3]$ に属している順序対は $(m+3,m)$ という形をしている。 $[-3]$ に属している順序対は $(n,n+3)$ という形をしている。 両方を加えると、 $$ \begin{align*} (m+3,m) + (n,n+3) &= ((m+3)+n, m+(n+3)) \\ &= ((m+n)+3, (m+n)+3) \\ \end{align*} $$ ということになる。結果の順序対は、 $$ ((m+n)+3, (m+n)+3) $$ になるから、 $[0]$ の要素になる。うまく行くわけだね」

ユーリ「おもしろーい」