![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの物理ノート/波の重ね合わせ』として書籍化されています。
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。好奇心旺盛で根気強い《元気少女》。
ここは高校の図書室。
僕は後輩のテトラちゃんに、先日ユーリに話していた《波の式》を説明していた(第142回参照)。
僕「……だから、この式だと時刻 $t$ の係数にマイナスが付くことになるんだよ。 ちょっとわかりにくいかもしれないけど」
テトラ「それは時刻 $t$ だけ《さかのぼった》ところにあった水位を見ているということになるんですね?」
僕「うん、だから、この波では《位置 $x$ の係数》と《時刻 $t$ の係数》は異符号になる。 これが《波の高さ》《波の波長》《波の周期》を全部入れた数式になるんだ。いわば《波の式》だね」
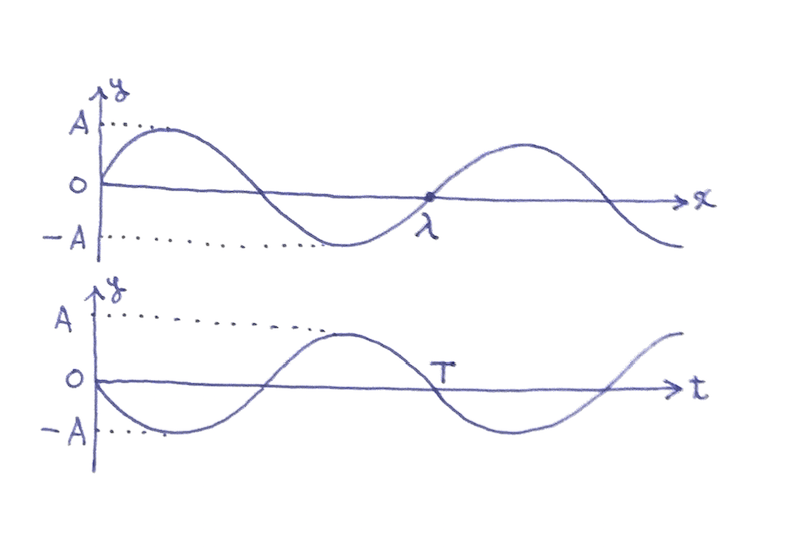
《波の式》
サインカーブで表される波を表す式は以下の通り。 $$ y = A \sin\left\{ 2\pi\left(\dfrac{x}{\lambda} - \dfrac{t}{T}\right)\right\} $$
ただし、
テトラ「それにしても、こんな難しい話をユーリちゃんは理解しちゃうんですか……」
僕「そうだね。えらいと思うよ。 あ、そういえば、センター試験に、ちょうどこの波の式が出たよね。上下反転してるけど」
テトラ「え! センター試験の、物理ですか?」
僕「物理の必答問題になってたね。 波の基本的理解を試すための問題ということだろうね」
テトラ「基本……これが基本なんですね」
僕「うん。だから、ちゃんと波を考えられるなら、 すぐに解けるよ。いっしょに解いてみようか」
テトラ「はい!」
平成28年度大学入試センター本試験 物理 第1問(平成28年1月17日実施)【一部修正あり】
$x$ 軸の正の向きに速さ $2$ m/sで進む正弦波がある。 図3は $x = 0$ における、変位 $y$ 〔m〕と時刻 $t$ 〔s〕の関係を表している。 位置 $x$ 〔m〕における、時刻 $t$ 〔s〕での変位 $y$ 〔m〕を表す式として 最も適当なものを、下の(1)〜(8)のうちから一つ選べ。

(1) $y = 0.2 \sin \left\{ \pi\left(t + 2x\right) \right\}$
(2) $y = 0.2 \sin \left\{ \pi\left(t - 2x\right) \right\}$
(3) $y = 0.2 \sin \left\{ \pi\left(t + \dfrac{x}{2}\right) \right\}$
(4) $y = 0.2 \sin \left\{ \pi\left(t - \dfrac{x}{2}\right) \right\}$
(5) $y = 0.2 \sin \left\{ 2\pi\left(t + 2x\right) \right\}$
(6) $y = 0.2 \sin \left\{ 2\pi\left(t - 2x\right) \right\}$
(7) $y = 0.2 \sin \left\{ 2\pi\left(t + \dfrac{x}{2}\right) \right\}$
(8) $y = 0.2 \sin \left\{ 2\pi\left(t - \dfrac{x}{2}\right) \right\}$
僕「まず、このグラフは《時刻と変位のグラフ》になっていることに注意して、 波の基本的な情報を集めていくよ」
テトラ「基本的な情報……周期や波長ですね?」
僕「そうそう。波一つ分を見てみると、 $2$ 秒だから、この波の周期は $T = 2$ ということになる。これはいいよね。 《時刻と変位のグラフ》から読み取れる」
テトラ「はい、そうですね」
僕「それから、波の高さ $A$ も読み取れる」
テトラ「はい、 $A = 0.2$ になっています」
僕「次に、問題文には速さが $2$ と書いてある。 向きは $x$ 軸の正の向きなので、速度 $v = 2$ といえる。 速度 $v$ と周期 $T$ がわかっているから、速度と周期と波長の関係式、 $$ v = \dfrac{\lambda}{T} $$ を使って、波長 $\lambda$ が求められることになる。これも難しくはない」
$$ \begin{align*} \lambda &= vT \\ &= 2 \times 2 && \REMTEXT{$v = 2, T = 2$だから} \\ &= 4 \\ \end{align*} $$テトラ「はい、波長は $\lambda = 4$ になりました」
僕「あとはさっきの《波の式》に代入すればいいんだけど、 注意が一つ要る。それは僕たちの《波の式》を作ったときと、 この入試問題では前提条件が違うということ。 《時刻と変位のグラフ》がちょうど上下反転しているんだよ。 だから $\sin$ の符号が反転する」
僕たちの《波の式》を作ったときの《時刻と変位のグラフ》
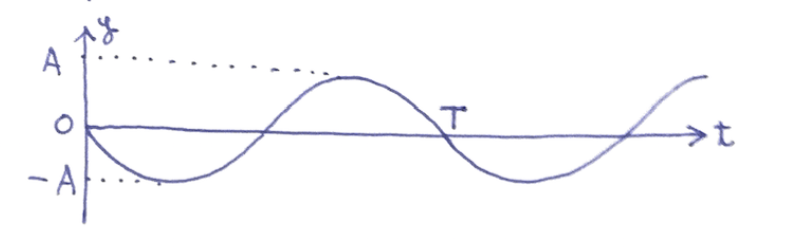
センター試験の問題の《時刻と変位のグラフ》(上下反転している)

テトラ「あれ、でも、この式は選択肢にありませんが……」
選択肢
(1) $y = 0.2 \sin \left\{ \pi\left(t + 2x\right) \right\}$
(2) $y = 0.2 \sin \left\{ \pi\left(t - 2x\right) \right\}$
(3) $y = 0.2 \sin \left\{ \pi\left(t + \dfrac{x}{2}\right) \right\}$
(4) $y = 0.2 \sin \left\{ \pi\left(t - \dfrac{x}{2}\right) \right\}$
(5) $y = 0.2 \sin \left\{ 2\pi\left(t + 2x\right) \right\}$
(6) $y = 0.2 \sin \left\{ 2\pi\left(t - 2x\right) \right\}$
(7) $y = 0.2 \sin \left\{ 2\pi\left(t + \dfrac{x}{2}\right) \right\}$
(8) $y = 0.2 \sin \left\{ 2\pi\left(t - \dfrac{x}{2}\right) \right\}$
僕「うん。だから、ここから三角関数の知識を使って式変形するよ。 $\sin$ は奇関数で $-\sin \theta$ は $\sin(-\theta)$ に等しい」

テトラ「そうですね」
僕「だから、式の初めのマイナスは、 $\sin$ の中に入れることができる。 角度に移せるんだよ。だから、こうなる」
$$ \begin{align*} y &= -0.2 \sin\left\{ \pi \left(\dfrac{x}{2} - t\right) \right\} \\ y &= 0.2 \sin\left\{ - \pi \left(\dfrac{x}{2} - t\right) \right\} && \REMTEXT{マイナスを中に入れた} \\ y &= 0.2 \sin\left\{ \pi \left(t - \dfrac{x}{2} \right) \right\} && \REMTEXT{さらに中に入れた} \\ \end{align*} $$テトラ「ということは、(4)が正解なのですね!」
僕「うん、そうだね」
テトラ「でも……これは、この《波の式》を暗記していないと難しくないでしょうか」
僕「暗記は必要だけど、条件がちょっと変わったら対処できなくなる丸暗記はだめだよ。 式の成り立ちを理解しておかなくちゃ。 全体の式の形が、 $y = A \sin \heartsuit$ という形になることはわかるよね」
テトラ「あ、はい。これはサインカーブ前提ということですから」
僕「センター試験の問題文でも《正弦波》と書いてあるからね。 それで、この $A\sin\heartsuit$ のうち、 $\heartsuit$ の部分……これを《位相》というんだけど、 これを $t$ と $x$ を使って表現したいわけだ」
テトラ「はい、そうですね」
僕「波一つ分動かすためには、 $\heartsuit$ を $2\pi$ 動かすことになるよね。サインカーブの波一つ分。 $t$ で動かすには、周期との比を考えて $2\pi \cdot \dfrac{t}{T}$ を使うし、 $x$ で動かすには、波長との比を考えて $2\pi \cdot \dfrac{x}{\lambda}$ を使う」
テトラ「あ、はい、それもわかるんですが、でも、あたし、符号をまちがう自信があります! ぜったいまちがいます!」
僕「テトラちゃん、まちがう自信って……うん、結局ね《波の式》は、 $$ y = A \sin\left\{2\pi\left(\pm \dfrac{x}{\lambda} \pm \dfrac{t}{T} \right)\right\} $$ という形になるんだから、あとは試しにちょっと動かしてみればいいんだよ。そうすれば符号のミスはかなり減らせるはず」
テトラ「動かすって、波をですか?」
僕「《時刻と変位のグラフ》が $y = \sin t$ のサインカーブと同じ形になるなら、 $t$ の符号はプラスだし、 上下反転したサインカーブなら $t$ の符号はマイナスとわかる。 つまり $t$ を $0$ からちょっと動かしてみて、頭の中でグラフを描くんだよ」
テトラ「ああ……」
僕「同じように《位置と変位のグラフ》を使って $x$ の符号がプラスかマイナスかわかる。ちょっと $x$ を動かしてみればいい」
テトラ「……でも、やはり三角関数には慣れてないといけませんね」
僕「そりゃそうだね。どういう式を立てたとしても、 この二つのグラフを使って確かめるときは、いまのようなチェックをすることになるんだよ。 だから、波で大事なのは、 与えられた条件からきちんと《時刻と変位のグラフ》と《位置と変位のグラフ》を描ける力なんだ。 そしてそれは、波の形を描く力ともいえる。理解していたらグラフがさっと描ける」
テトラ「わかりました!」
僕「もしどうしても忘れちゃったら、 とりあえず目の前のグラフからわかることだけを書くのも手だよ。 問題文にあるこの《時刻と変位のグラフ》の式は、 $$ \begin{align*} y &= 0.2 \sin \left\{ 2\pi \cdot \frac{t}{T} \right\} \\ &= 0.2 \sin \left\{ 2\pi \cdot \frac{t}{2} \right\} \\ &= 0.2 \sin \pi t \end{align*} $$ という形になってる。ということは、 与えられた選択肢 $8$ 個のうち、 $t$ の係数が $2\pi$ になっているものは除外できるわけだね」
テトラ「ははあ……これは、 $x = 0$ のときのグラフですものね」
僕「そういうこと。もっとも、そこから先は何をどう考えようとも、《時刻と変位のグラフ》と問題文から、 《位置と変位のグラフ》を描くのと同じようなことを考える必要があるけれどね。 確実に解くためには結局、波の動きと式の意味をきちんと理解しておくしかないんだよ」
テトラ「はい!」
テトラ「……ところで、波というと、何となく想像はできるんですけど、 《時刻と変位のグラフ》と《位置と変位のグラフ》の二種類を考えることができる、 という発想はありませんでした」
僕「そうだよね。僕も物理で習うまでそんなこと、意識もしなかったよ」
テトラ「横軸は違いますが、縦軸はどちらも変位なのですね」
僕「そうだね。水の波だったら水位だろうけど、一般的には変位というね」
テトラ「一般的には……先輩、音はどうなるのでしょう」
僕「音も波だよ」
テトラ「ええ、そうですよね。音も波で、空気の振動が伝わっていくのは知っているんですが、 でも、水の波とは違うように思います。水の波ですと、水の下の世界と水の上の世界があります。 そしてその境目が波として見えています。でも、音は? 空気の振動は……」
僕「ああ、そうだね。テトラちゃんのいうとおり、 水の波と音の波は違うよ。それは《横波》と《縦波》の違いになるのかなあ」
テトラ「あっ、横波と縦波という言葉は聞いたことがあります。 地震のニュース解説でちらっと」
僕「横波か縦波かというのは、 《波の進行方向》と《媒質の振動方向》の違いを表現しているんだよ、 テトラちゃん」
テトラ「波と媒質……ですか」
僕「波がまっすぐ前に進んでいくとするよね。それを《波の進行方向》と呼ぶとしよう」
テトラ「波の進行方向はこっち! のようにですか」
テトラちゃんはそういって、右手をさっと前に伸ばす。
僕「そうそう。たとえば水の波が進んでいくとして、媒質、つまり水は上下に振動しているよね」
テトラ「はい、そうですね」
テトラちゃんはそういって、伸ばした手を上下に動かす。
僕「そういう波のことを《横波》っていうんだ。 波の進行方向を基準として、媒質の振動方向は《横》になっているから」
テトラ「上下なのに、横……なんですか?」
僕「ああ、ちょっと混乱しやすいよね。 《波の進行方向》に対して《媒質の振動方向》が垂直ということなんだ。基準の方向との関係。 うん、そうだ、洋服の横縞と縦縞を考えればいい。 自分の身体を棒だと考えると《横縞》というのは、 その棒に垂直の向きの縞模様のことだよね?」
テトラ「あっ、はい、そうですね。横のボーダー柄のことですね」
僕「あれと同じ。水の波が進む方向に対して水は垂直に振動している。 だから、水の波は横波というわけ」
テトラ「わかりました! 横のボーダー柄の服を着て水泳しているようなものですね!」

僕「あはは、そうだね。泳ぐ方向が《波の進行方法》で、横縞の方向が《媒質の振動方向》に対応してる。横波だ」
テトラ「あれ、でも、縦波は?」
僕「縦波は《波の進行方向》に対して《媒質の振動方向》が平行になるような波のことだね。 音の波は縦波になる。水の波は横波で、音の波は縦波」
テトラ「う、うう……波の進行方向と、媒質の振動方向が平行というのが、 想像できませんっ!」
僕「たとえば、こんなふうに媒質を単純化して描いてみるよ。 媒質が振動していないとき、つまり波がない状態では、 こんなふうに等間隔で並んでいるとする」

テトラ「おとなしく?」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2016年1月22日)
この記事は『数学ガールの物理ノート/波の重ね合わせ』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!