![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの物理ノート/波の重ね合わせ』として書籍化されています。
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだけれど飽きっぽい。
僕とユーリは《波》についておしゃべりしている。
僕「じゃあ、ここでユーリに問題を出すよ」
ユーリ「どんとこい」
僕「この波の速度を $v$(ヴィ)としたとき、 《速度 $v$》を《波長 $\lambda$(ラムダ)》と《周期 $T$》で表せ。これが問題」
問題1(波の速度・波長・周期)
以下のグラフは、ある波を表している。 この波の速度を $v$ としたとき、 $v$ を $\lambda$ と $T$ で表せ。
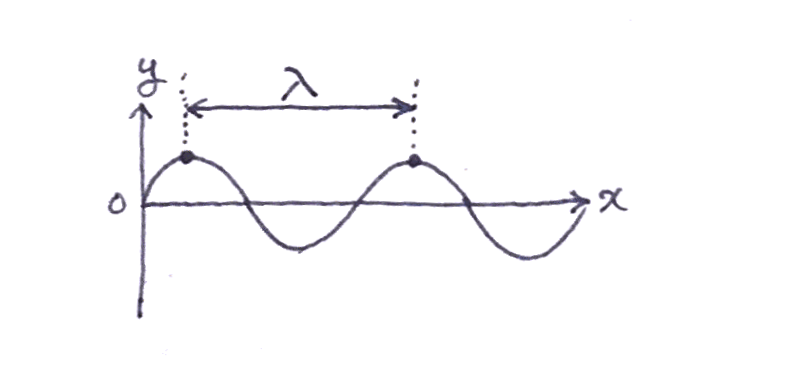
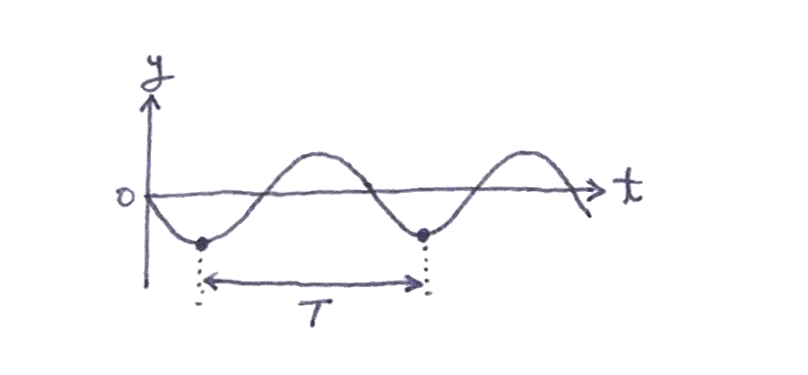
ユーリ「むむむ? 波の速度?」
僕「さあどうかな」
ユーリ「……これって、わかるの?」
僕「わかるよ。波長 $\lambda$ と周期 $T$ がわかっていれば、 波の速度 $v$ を求めることができる。もう少しいえば、 $\lambda$ と $T$ を使った式で、 $v$ を書き表すことができるんだよ」
ユーリ「速度……えーと」
僕「そんなに難しくないと思ったんだけど」
ユーリ「うーん……よくわかんなくなった。波長って波の $1$ 個分の長さで、 周期は波が一回波打つのに掛かる時間だよね。 ほんとにその二つで表せるの?」
僕「表せるよ。……もしかしたら、ユーリは《波が動いていくようす》を頭の中で想像できていないんじゃない? さっきのこの図を思い出せばわかると思うんだけど。 ほら、波の山がずっと動いていく様子」
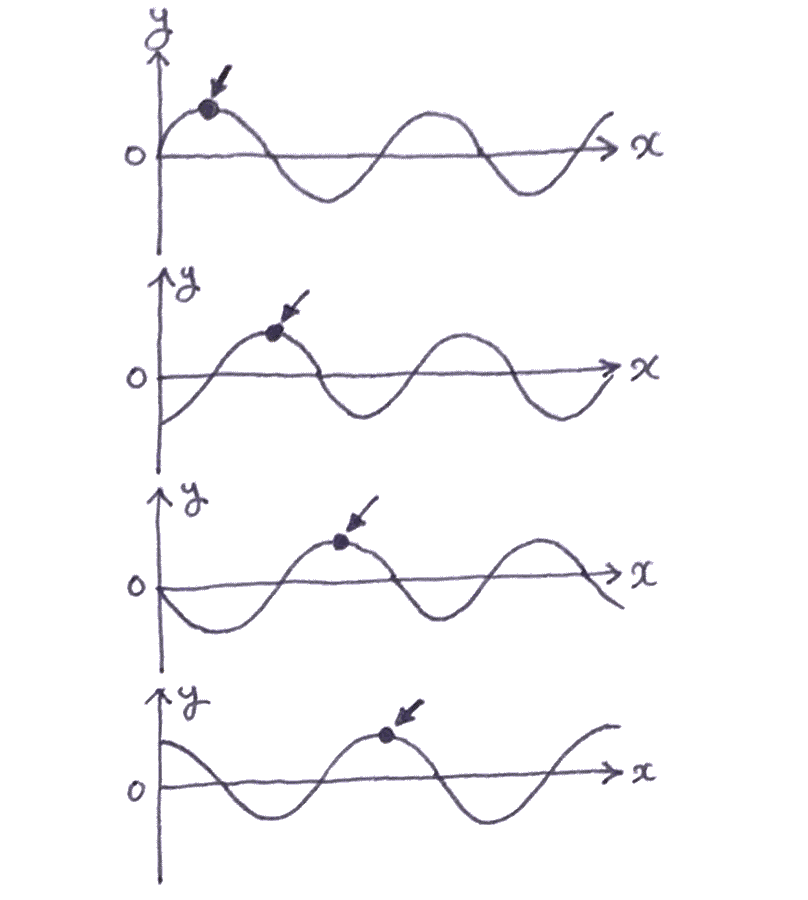
ユーリ「想像できてるよ! でも、波を考えてると、わかんなくなっちゃうの!」
僕「速度は《位置の変化》を《時刻の変化》で割れば求められるよね。 《位置の変化》はどのくらい動いたかで、 《時刻の変化》はその動きにどれだけ時間が掛かったか」
ユーリ「そーだけど」
僕「たとえば、この波の《山》が、波長 $1$ 個分だけ動いたとしよう。 つまり《位置の変化》が $\lambda$ だということ」

ユーリ「……うん」
僕「そのときの《時刻の変化》は? つまり、 《山》が $\lambda$ だけ動くのに掛かった時間はどれだけ?」
ユーリ「……もしかして、周期? だから、掛かった時間は $T$ ?」
僕「そうだよ! なんだ、わかっているじゃないか。 《山》の位置が $\lambda$ だけ動くとき、掛かる時間は $T$ になる。 《山》の速度はもちろん波の速度に等しいから、 $$ v = \dfrac{\lambda}{T} $$ ということになる」
ユーリ「そっか……それでいーのか……」
僕「$\lambda$ は長さだから、単位はmやcmなどになる。 $T$ は時間だから、単位は秒や分などになる。 $\dfrac{\lambda}{T}$ の単位は「長さを時間で割ったもの」だから、 確かに速度の単位になってる。 物理量を考えるときには、次元も確かめておかないとね」
ユーリ「……」
僕「なに?」
ユーリ「さっきの、まだ考えてたの。 どーして波の速度が $\dfrac{\lambda}{T}$ なんだろって」
僕「お?」
ユーリ「あのね、《長さを時間で割ればいい》っていうのはわかってたよ、ユーリも。 波長は長さだし、周期は時間だから、きっと波長を周期で割ればよさそーだな、とも思ったの。 でも、うそっぽくて」
僕「うそっぽいとは」
ユーリ「だって、リクツがわかってないもん! 長さになってるものがありますー、時間になっているものもありますー、 だったらきっと、これをこれで割れば速度ですねー……そんなの、 うそっぽいじゃん!」
僕「なるほど。ユーリはバシッと理解したいってことなんだね。 ちゃんと納得して。ところで、もう理解できたのかな」
ユーリ「少しは。あのね。ユーリは《波の速度》と《水の速度》 がまざってたみたい」
僕「へえ」
ユーリ「波のようすを想像するじゃん? そのときに、 さっきお兄ちゃんが描いてくれたように、《山》が動くようすを想像してなかったの。 そうじゃなくて、水が上下に振動しているのを想像してた」
僕「ああ……なるほどね。その上下の動きの速度について考えちゃったわけか」
ユーリ「たぶん。だからね、波長と周期だけじゃわかんなくて、 波の高さ?大きさ?みたいなのを考えないと、速度は求められないって思ったの」
僕「なるほど! ユーリの考えていたことはよくわかった。 高い波を作っている水がすごいスピードで落ちてくるのと、 低い波を作っている水がゆっくり落ちてくるのとじゃ速度が違う……って考えちゃったんだね」
ユーリ「そーみたい」
僕「うん、いま僕たちがいっしょに考えようとしてたのは、 水が動く速度じゃないからね。 媒質の動く速度じゃなくて、波という現象の速度の方を考えていたんだ。 《波の速度》というのは、つまり《振動が伝わっていく速度》ということになるよね」
ユーリ「うん! もう納得したからまちがわないよ!」
僕「それにしても、《自分がどういうふうに誤解したか》を説明するというのは、 すごく高度な技だと思うよ。ユーリ」
ユーリ「そーかにゃ? 照れるじゃん!」
解答1(波の速度・波長・周期)
以下のグラフが表す波の速度を $v$ としたとき、 $$ v = \dfrac{\lambda}{T} $$ が成り立つ。


僕「波は、位置と時刻が絡んでくるから、難しいんだよ」
ユーリ「もうユーリは理解したから、難しくないよ」
僕「そのまっすぐな自信はどこから来るんだろう。すごいな」
ユーリ「試しに問題出してみてよ」
僕「じゃあね、こんな問題はどうだろう」
問題2
以下の四枚のグラフがある。 (1)は $t = 0$ であるとする。 このとき、(2),(3),(4)のグラフでの $t$ を求めよ。 ただし、この波の周期は $T$ とする。

ユーリ「えっと……なーんだ、カンタンじゃん!」
僕「おっと、早いな。もうわかったの?」
ユーリ「周期 $T$ ってゆーのは、波の $1$ 個分に掛かる時間なんだから、 $T$ だけ時間が過ぎたら、もとに戻るんでしょ? だったら、 これは $\dfrac{T}{4}$ ずつ時刻が進んでるってことじゃん!」
僕「ほほう」
ユーリ「だから、 (2)は $t = \dfrac{T}{4}$ で、 (3)は $t = \dfrac{T}{2}$ で、 (4)は $t = \dfrac{3T}{4}$ でしょ?」
僕「すごいすごい! 大正解だよ!」
ユーリ「ふふん」
解答2
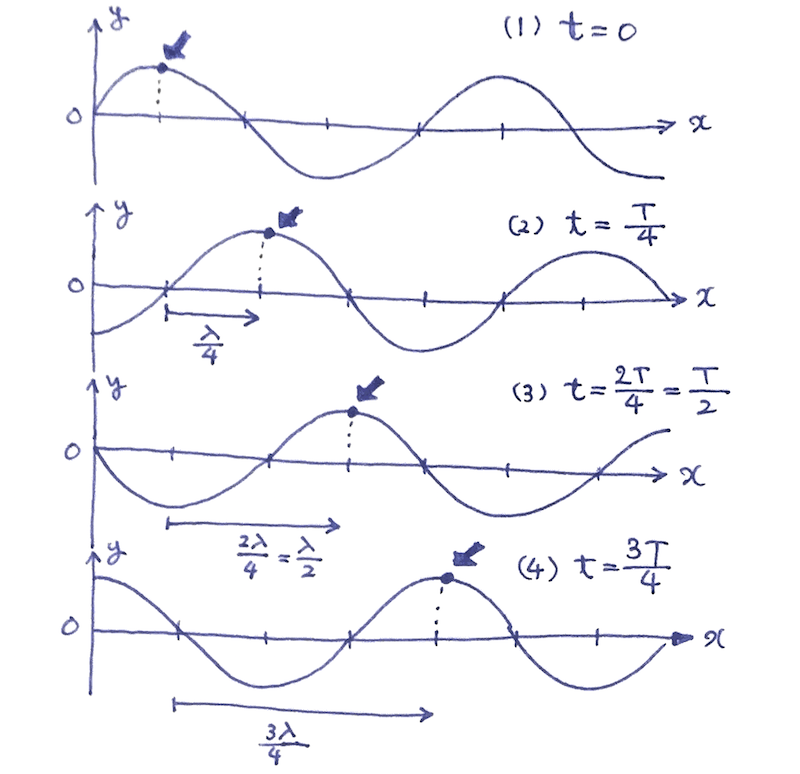
僕「だから、 《位置と水位のグラフ》を見れば、 そこに歴史が刻まれていることがわかるんだよ」
ユーリ「え、お兄ちゃん、いま何て言った?(にやにや)」
僕「いや、ちょっと……茶化すなよ。 つまりね、《位置と水位のグラフ》というのは、 位置 $x$ に対する水位 $y$ を表しているよね。 そして、位置 $x$ での水位 $y$ っていうのは、 過去からの波がやってきたことで、その水位が決まったわけだ」
ユーリ「まーね」
僕「だから、《位置と水位のグラフ》で波が右方向に進んでいるとしたら、 右に行けば行くほど、過去の水位がそこに反映しているし、 左に行けば行くほど、未来の水位がどうなるかわかることになる」
ユーリ「何言ってるかわかんない」
僕「つまり、こういうことだよ。 《位置と水位のグラフ》で波長 $\lambda$ だけ左右を見ると、 それは周期 $T$ だけ未来や過去を見ているということ」

ユーリ「あたりまえじゃん! それが波長と周期ってことだし」
僕「うう……あたりまえか……理解したユーリ最強だな」
ユーリ「ふふん」
僕「ところでこれから考えたいのは《波を数式で表す》ことだよ」
ユーリ「出たな数式マニア。さっき $\dfrac{\lambda}{T}$ で表したばっかりじゃん」
僕「それは、波の速度 $v$ を波長 $\lambda$ と周期 $T$ で表しただけだろ。 そうじゃなくて、波の全体を数式で表したい。 具体的にやりたいことは、位置 $x$ と時刻 $t$ を与えると水位 $y$ がわかるような数式を作りたいんだ」
ユーリ「ふーん……位置と時刻から水位?」
僕「そうだね。ただし、いろいろ決めないと数式は作れない。 たとえば《波長を $\lambda$ とする》とか《周期を $T$ とする》とか。 他には何を決める必要があるだろう」
ユーリ「速度?」
僕「いや、速度は波長と周期から決まるから、 わざわざ決めなくてもいい。 あとは《波の高さ》かな。大きな波と小さな波は違うから。 たとえば《波の高さを $A$ で表す》としよう」
ユーリ「……」
僕「そして、大前提として《波の形はサインカーブ》ということにしよう。 とても基本的な波の形として、サインカーブを使う」
問題3(波を数式で表そう)
波がサインカーブで表せると仮定し、位置 $x$ で時刻が $t$ のときの水位を $y$ とする。 $y$ を $x$ と $t$ の式で表せ。
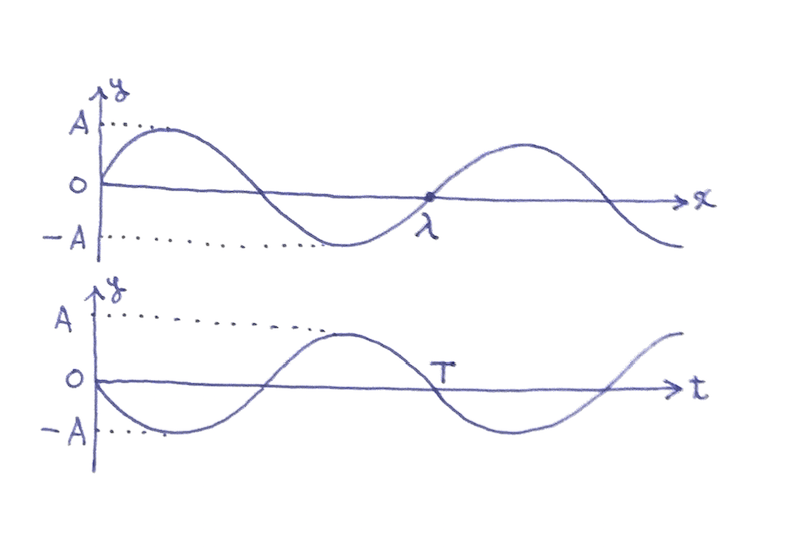
ただし、
僕「ユーリは $\cos$ と $\sin$ は覚えている?」
ユーリ「何となく。コサインとサイン。あのほら、円の $x$ と $y$」
僕「そうだね。半径が $1$ の円のことを単位円といって、 その円周上の点 $P$ を考える。点 $P$ と中心を結んだ半径が、 $x$ 軸の正の向きとなす角度を $\theta$ としたとき、 点 $P$ の $x$ 座標が $\cos \theta$ で、 $y$ 座標が $\sin \theta$ になる」
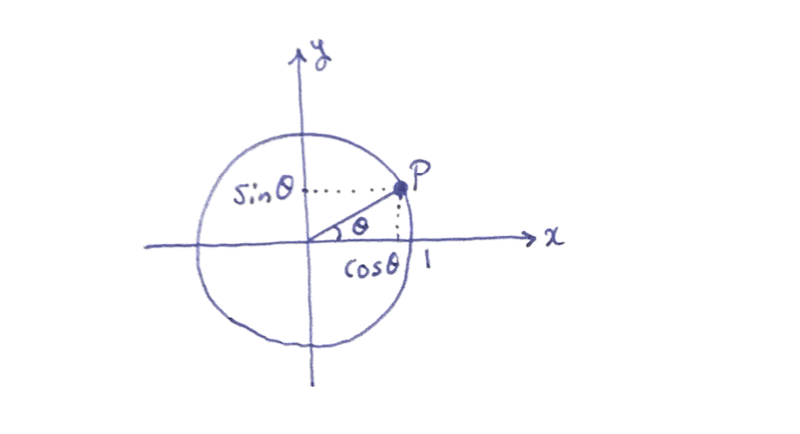
ユーリ「サインカーブ、思い出してきた」
僕「うん。横軸を $\theta$ としたとき、 $y = \sin \theta$ のグラフはこうなるね」
$y = \sin\theta$ のグラフ
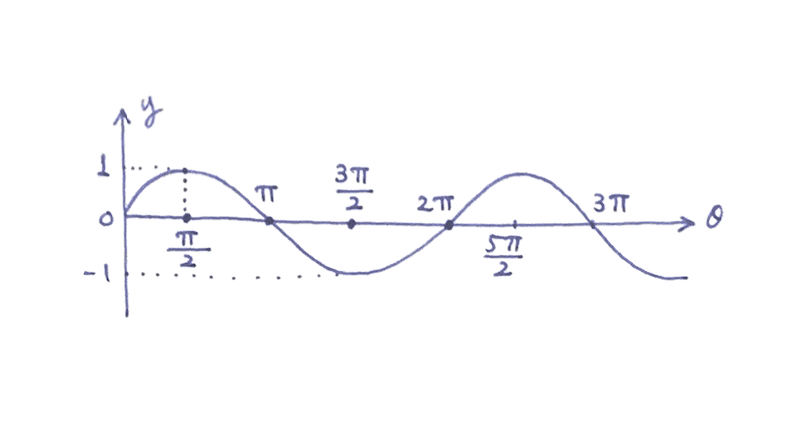
ユーリ「そっか、波なんだ……」
僕「波だね。このグラフは $y = \sin \theta$ という数式で表されている。 つまり、角度 $\theta$ を与えると、 $y$ が決まるわけだ。 $\sin$ という関数でね」
ユーリ「そだね」
僕「これから、 $y = \sin \theta$ のグラフを、 僕たちが作りたい形に変形させていくよ」
ユーリ「グラフを変形させる?」
僕「そう。このサインカーブのグラフを変形させていく。 具体的には $y = \sin \theta$ という数式を少しずつ変えていく。 そして僕たちのゴールは、 波長が $\lambda$ で、周期が $T$ で、 高さが $A$ であるような波の数式を手に入れること!」
ユーリ「盛り上がっているトコ悪いんだけど、 それってめちゃめちゃ難しー話じゃないの?」
僕「そんなことないよ」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2016年1月15日)
この記事は『数学ガールの物理ノート/波の重ね合わせ』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!