![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/積分を見つめて』として書籍化されています。
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。好奇心旺盛で根気強い《元気少女》。
僕「テトラちゃん、それ、何?」
ここは僕の高校の図書室。いまは放課後。 机に向かったテトラちゃんが、《カード》をくるくる回すようにしてながめている。
テトラ「あ、先輩! これ……村木先生の《カード》なんですけど」
数学の村木先生は、僕たちにときどき《カード》をくれる。
問題が書かれているときもあるけれど、
数式が一つだけ、ぽつんと書かれているときもあるし、
色とりどりの《カード》の束が来ることもある。
僕たちはそこから好きなように考えを広げ、数学トークをする。
そして、気が向けば自由にレポートを書く。
いや、成績がつくわけじゃない。これは、僕たちの《おたのしみ》なのである。
僕「それで、どんな問題?」
テトラ「それが、何も書かれていないんです。まっ白で、しかも《丸い》んです!」
僕「丸い?」
僕はテトラちゃんから《カード》を受け取る。
確かに、お皿みたいに丸いなあ。
直径は、ノートの幅と同じくらいかな。
村木先生の《カード》

僕「これは……珍しいな。 そもそもカードが《丸い》のは初めてじゃないかなあ」
僕はカードをテトラちゃんに返す。
テトラ「それでですね、あたしは、何か《すかし》のようなものが書かれているのかな……と調べていたんです。 こうやって……」
テトラちゃんは、カードを両手で持ち上げる。
僕「あ、テトラちゃん! そのカードをそのまま、ずっと上に……」
テトラ「え? こ、こうですか?」
僕「そうそう。両手で持ったまま、頭の上に、水平にして……違う違う。 頭に乗せるんじゃなくて、頭の上にふわっと浮かせる感じに。そうそう!」
テトラ「こうでしょうか?」
僕「そう、そしてそのまま微笑んで!」
テトラ「あ、はい」
素直なテトラちゃんは、白くて丸いカードを両手で持ち、頭の上に浮かせると、にっこりと微笑む。
僕「うんうん」
テトラ「これは……数学のどんな問題になるんですか?」
僕「あ、違うんだよ。そうやっていると、テトラちゃんはまるで《天使》みたいだなって」
テトラ「も、もう! からかうのはやめてくださいっ!」
僕「ごめんごめん。ところでこのカードなんだけど、村木先生はなんて言ってたの?」
テトラ「は、はい……あたしが積の積分のこと(第138回参照)をレポートにして持っていったら、 先生はこれを渡してくださったんです」
僕「じゃあ、これは積分しろという話なのかな」
テトラ「円を積分?」
僕「きっと円の面積を求めよということなんじゃないかなあ」
テトラ「円の面積……というのは $\pi r^2$ ですよね」
僕「そうだね。円周率を $\pi$(パイ)で表すと、 半径が $r$ の円の面積は $\pi r^2$ で求められる。円の面積を表す公式はそうなる」
円の面積を表す公式
円周率を $\pi$ で表すと、半径が $r$ の円の面積 $S$ は、 $$ S = \pi r^2 $$ で求められる。
テトラ「はい。これは小学校のときに習いました。$\REMTEXT{半径} \times \REMTEXT{半径} \times 3.14$ です」
僕「うん、そうだよね。小数の掛け算がめんどうだったの思い出すなあ」
テトラ「公式を説明なさった先生の図が衝撃的でした」
僕「図?」
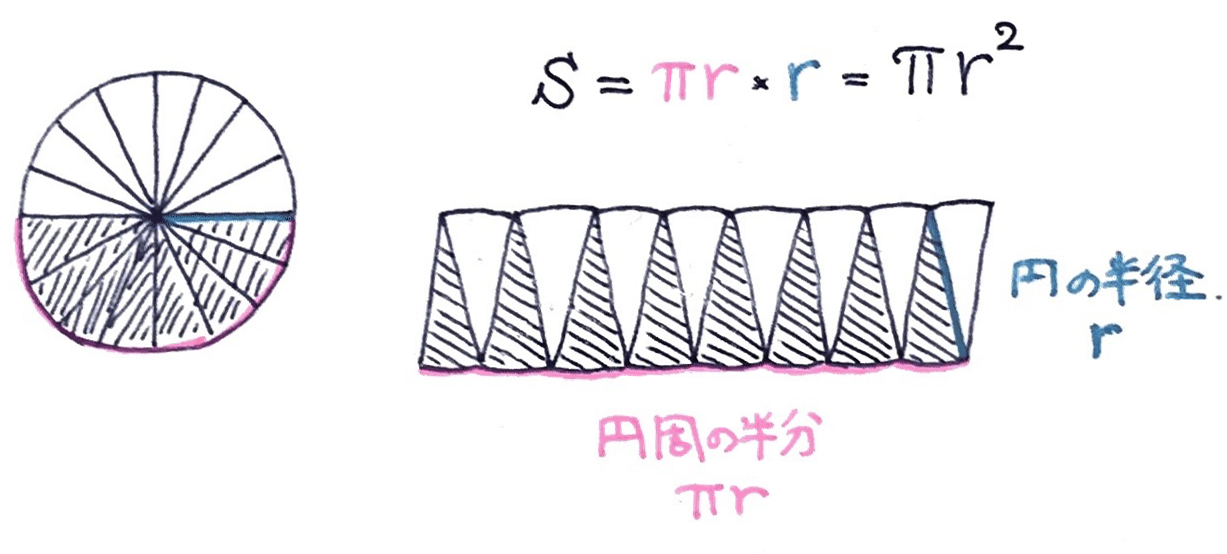
テトラ「そうです。円形のピザをたくさんの扇形に切って、組み替えて、平行四辺形のような形にしていくんです」
僕「ああ、そうだったね。こんな図だよね。たとえばピザを $8$ 枚に分割した場合」
円形のピザを $8$ 枚の扇形に分割して組み替える

テトラ「そうです、そうです。そして、その扇形をした《ピザ $1$ 切れ》をどんどん細くしていくと、 《底辺の長さ》は《円周の半分》で、 《高さ》は《円の半径》に近づいていくから、円の面積が求まる……と」
僕「うんうん、なつかしいなあ」
テトラ「でも、何だかちょっとごまかされた感じがしました。 だって、《ピザ $1$ 切れ》をいくら細くしても、底辺は少しだけ《でこぼこ》しますよね。その《でこぼこ》はどうなるのか……と疑問でした」
僕「小学校や中学校だと、《極限》のことはそうやって説明するしかないんだけどね」
テトラ「極限……あの $\lim$ ですね?」
僕「そうだね。数列の極限、関数の連続、関数の微分、そして積分……と、 数学のあちこちには極限が出てくる。面積を求めるときもね」
テトラ「……」
僕「どうしたの?」
テトラ「もしかして、いまなら……高校生のいまなら、 あのピザの謎が解けるということでしょうか。《極限》で?」
僕「そういうことになるね。確かに極限を計算すると $\pi r^2$ になるってわかるはず」
テトラ「先輩は、もうご存じなんですか? ピザを使った円の面積の求め方」
僕「ええと、うん、そうだね。数学の本に出てきたから、式を追いかけたことがあるよ。 その後、何回か自分でもノートに再現できたから、たぶん理解していると思う。 いっしょに《円の面積の公式》を求めてみようか」
テトラ「はい!」
僕「問題をきちんと書くと、こうかな」
問題
半径が $r$ の円の面積が、 $\pi r^2$ で求められることを証明せよ。
(ピザの分割と、極限を使う)
テトラ「はい」
僕「僕たちはピザを分割して《ピザ $1$ 切れ》をどんどん細くしていき、 その極限をとって円の面積を求めようとしているんだよね」
テトラ「はい、そうですね」
僕「ということは、最後の極限に持っていくときのために、 ピザ……つまり《円を $n$ 分割する》ことにしよう」
テトラ「なるほどです。そして、 $n$ を大きくしていくんですね?」
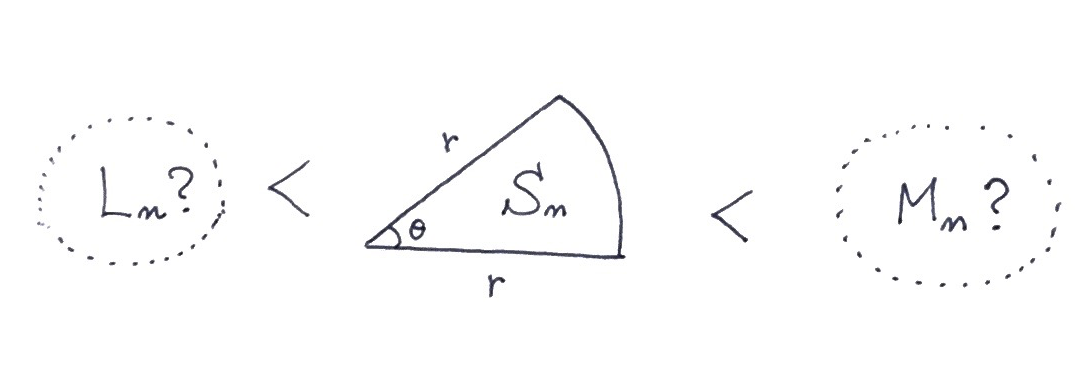
僕「そうだね。 $n \to \infty$ の極限を考えることになる。 ピザを $n$ 分割したときの《ピザ $1$ 切れ》の扇形の面積を求めることになるから……うん。 半径 $r$ の円の面積を $S$ として《ピザ $1$ 切れ》の面積を $S_n$ としよう。 図に描くとこうなるね」
$n$ 分割した《ピザ $1$ 切れ》

僕「中心の角度を $\theta$(シータ)とすると、ぐるっと一回りする $360$ 度、つまり $2\pi$ ラジアンを $n$ 等分しているわけだから、 $$ \theta = \dfrac{2\pi}{n} $$ になるね」
テトラ「なるほどです。 はい、扇形の面積 $S_n$ を求めてそれを $n$ 倍すれば円の面積 $S$ になるということで……でも、先輩、 その《扇形の面積》を《円の面積》から求めてはだめですよね?」
僕「だめだね。それでは循環論法になってしまうから。 使える道具は《はさみうち》だよ。 《ピザ $1$ 切れ》の扇形をはさむような、《二つの形》を見つければいいはず」
テトラ「二つの形?」
僕「一つは《ピザ $1$ 切れ》よりも明らかに《小さな形》で、一つは明らかに《大きな形》。 その《二つの形》の面積で《ピザ $1$ 切れ》の面積を《はさみうち》するんだよ。 そういう二つの形を見つけるんだ。《小さな形》の面積を $L_n$ として、 《大きな形》の面積を $M_n$ とすると、 $$ L_n < S_n < M_n $$ という不等式を作ることになるね」
《二つの形》を見つけよう
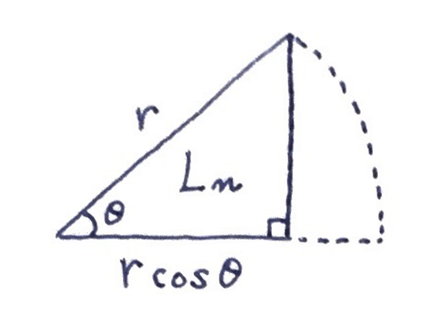
テトラ「ははあ……あ! 《小さな形》は見つかりますよ。こういう直角三角形でいいですよね?」
《ピザ $1$ 切れ》の扇形よりも明らかに《小さな形》となる直角三角形
僕「うん、いいね! これなら面積もすぐにわかるし。面積は……」
テトラ「テトラもわかります。斜辺が $r$ の直角三角形で、角度が $\theta$ なんですから、 底辺は $r \cos \theta$ で、高さは $r \sin \theta$ ですね。 ですから、面積は $\frac12 \cdot r \cos \theta \cdot r \sin \theta$ です!」
僕「そうなるね。この直角三角形の面積を $L_n$ と表すと、式を整理してこうなるかな」
《小さな形》

僕「それで、下はいいとして、上はどうするんだっけかな……」
テトラ「上? 《大きい形》のほうですね」
僕「うん、僕たちはいま $S_n$ を《はさみうち》したい。 テトラちゃんが見つけてくれた三角形 $L_n$ で小さい形はできそうだ。 $L_n < S_n$ だね。 《大きい形》の面積を $M_n$ として、 $$ L_n < S_n < M_n $$ とはさむ。そして……」
テトラ「あ!」
僕「あ!」
テトラ「先輩も見つけました?」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2015年11月27日)
この記事は『数学ガールの秘密ノート/積分を見つめて』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!