![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/積分を見つめて』として書籍化されています。
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだけれど飽きっぽい。
ユーリ「ねーお兄ちゃん、算数って変な問題あるよね」
僕「変な問題って?」
ユーリ「ほら、『水槽に水を入れるときに何分かかりますか』みたいなの」
僕「算数でよくある問題だね。でも何も変じゃないよ」
ユーリ「だってさ『実はその水槽には穴が開いていて、 水が決まった量だけ流れ出しています。さて』みたいなの……それって、 水を入れる前に穴ふさいだほーがいいじゃん!」
僕「ああ、そういうことね。ユーリの言いたいことはわかるけど。 算数の問題は自然に読めるときもあるけど、実際の生活に当てはめるとき、 おかしな場合は確かにあるなあ」
ユーリ「こないだね、テストで計算ミスして、 人間の歩くスピードが《時速300キロ》になった友達いたよ」
僕「あはは、そりゃおかしいな。新幹線より速い。でもそれは計算ミスだから、 出題者は悪くないよね」
ユーリ「それでも『水槽に穴が開いていて』っていうのはちょっとなー」
僕「そういえば、小学校のときすごく悩んだ問題があったな。 算数の問題なんだけど」
ユーリ「へー、どんなの?」
僕「話したことなかったっけ。水槽の問題だよ」
問題1(二本の管と水槽)
円筒形の水槽に水を入れましょう。
太い管と細い管の二本を使って水を入れることができます。
太い管だけを使ったときには、 $3$ 分で水槽はいっぱいになります。
細い管だけを使ったときには、 $6$ 分で水槽はいっぱいになります。
それでは、太い管と細い管の両方を使って水を入れたなら、 水槽は何分でいっぱいになりますか。
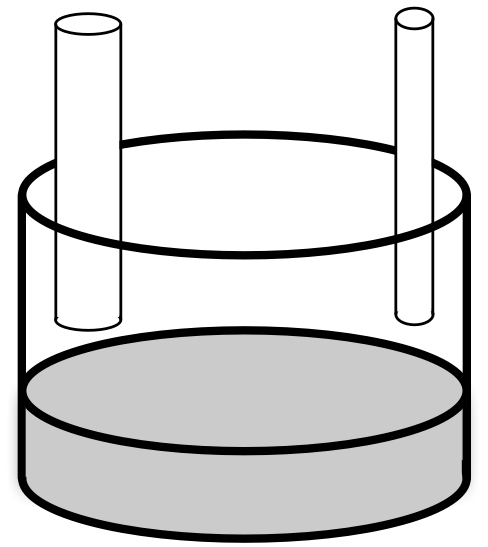
ユーリ「これ、難しーの?」
僕「ユーリだったらどうやって解く?」
ユーリ「普通に解けばいーんでしょ? 太いのが $\frac13$ で細いのが $\frac16$ で、 足したらえっと $\frac{9}{18}$ だから $\frac12$ なので、 $2$ 分。 $2$ 分でいっぱいになる!」
僕「早いな!」
ユーリ「へへ。難しくないじゃん」
僕「小学生のときのお兄ちゃんには難しかったんだよ」
ユーリ「へー、何でなんで? どこが難しかったの?」
僕「ユーリはいま一言で『太いのが $\frac13$』って答えたけど、 その $\frac13$ はどこから来たんだろう」
ユーリ「だって、太い管なら $3$ 分で水槽がいっぱいになるんだから、 $\frac13$ じゃん」
僕「うん、だから、その $\frac13$ という数はどこから、なぜ出てきたのか。 それが小学生のときのお兄ちゃんには納得いかなかったんだよ。 さっきの問題、ちゃんと答えるとこうだよね」
解答1(二本の管と水槽)
太い管だけを使ったときには、 $3$ 分で水槽の全体が水で満たされます。 だから、 $1$ 分では水槽の $\frac13$ が満たされます。
同じように、細い管だけを使ったときには、 $1$ 分で水槽の $\frac16$ が満たされます。
ということは、太い管と細い管の両方を使ったときには、 $1$ 分で水槽の $\frac13 + \frac16$ が満たされます。
$\frac13 + \frac16$ を計算します。
$$ \begin{align*} \frac13 + \frac16 &= \frac6{18} + \frac3{18} \\ &= \frac{6 + 3}{18} \\ &= \frac{9}{18} \\ &= \frac12 \\ \end{align*} $$
ですから、太い管と細い管の両方を使ったときには、 $1$ 分で水槽の $\frac12$ が満たされます。
よって、水槽全体が満たされるのは $2$ 分後です。
ユーリ「ユーリの答えであってるじゃん。 何にも難しくない」
僕「お兄ちゃんがね、そのころ引っかかってたのは、 《あれ? 水槽の大きさはどうなったんだろう》というところなんだよ。 問題を読んだとき、心の中に水槽を思い浮かべるよね。 水槽と、そこに水を入れる管二本を想像する」
ユーリ「そだね」
僕「$3$ 分で水槽がいっぱいになるとか、 $6$ 分で水槽がいっぱいになるとか、 そういうことも全部想像できる。 でも、いざ計算しようと思ったときに《水槽の大きさ》を求められない! と思ったんだよ。それで何だか納得いかなかった」
ユーリ「そーなんだ。お兄ちゃん、考えすぎんじゃないの?」
僕「でも、さっきの解答のように、『$1$ 分たったときどうなるか』を考えたら、 すごく納得した。つまり『$3$ 分でいっぱいになります』という問題文を、 『$1$ 分たった時点では $\frac13$ が満たされています』のように言い換える。 そこで大きなジャンプがあったんだね」
ユーリ「ジャンプって?」
僕「思考のジャンプ。考えの飛躍ってこと。 その言い換えができたとき、頭の中でカチカチカチっとつながった感じがしたんだ。 なぜかっていうと、 $1$ 分たった時点の状態を想像すると、
ユーリ「小学生のお兄ちゃんが?」
僕「いや、もちろん、そんなふうにきちんと考えたわけじゃなくて、 そう感じたということなんだけど」
ユーリ「へー、すごいね」
僕「そんなことないよ。でも、まだ引っかかっていることがあったんだ」
ユーリ「問題は解けたのに?」
僕「問題は解けたのに」
ユーリ「へー」
僕「あのね。さっきの問題は『$1$ 分後にどうなっているか』を想像すればわかる。 $\frac13$ と $\frac16$ を足すことができるからね。 でも、じゃあ、この $\frac13$ や $\frac16$ というのは何を考えていることになるんだろう…… そこが気になったんだよ。すごく便利な考え方だから」
ユーリ「小学生のときにそんなこと考えてたの?」
僕「いや、それはちょっと違うかも。 いまユーリに話したように整然と考えてたわけじゃない。 そんなふうに言語化してたわけじゃない。 もっとぼんやりと『これって何だろう』と考えてたという意味だよ」
ユーリ「んで、結論は?」
僕「そのときは結局ピンと来なかったんだけど、 『$1$ が大事』ということはわかった。つまりね、
ユーリ「ほーほー。『そのとき少年は気付いた、 $1$ が大事であることを』」
僕「なにナレーションやってるんだよ」
ユーリ「倒置法の練習」
僕「いまにして思えば、 『水槽全体を $1$ として考える』というのは《割合》を理解したってことだし、 『$1$ 分たったときのようすを想像する』というのは《速さ》を理解したってことなんだろうな」
ユーリ「速さ?」
僕「そうだね。正負の向きも考えていうなら、 《速度》を理解したってこと。『$1$ 分たったときにどれだけ水がたまったか』 というのは『単位時間あたりの水量』だから、水の速度といってもいいよね」
ユーリ「そゆことか。速度っていえば、 こないだお兄ちゃんから《微分》を教わったときに出てきた(『数学ガールの秘密ノート/微分を追いかけて』参照)」
僕「そうだね。 あのときは《単位時間あたりの位置の変化》で《平均の速度》を考えた」
ユーリ「グラフたくさん描いたよね」
僕「うん、あのときは接線の傾きで微分を……なるほど。 それはちょっとおもしろいかも」
ユーリ「なになに?」
僕「こんな問題はどうだろう」
問題2(?)
深さが $1$ mで、円筒形をした水槽に水を入れます。
太い管を使って水槽に水を入れると、 $3$ 分で水槽がいっぱいになります。
時刻を $t$ 分とし、 底面から測った水面の位置を $x$ メートルとし……
ユーリ「カンタン! だって、ずーっと水がたまっていくんだもん。 こんな感じ!」
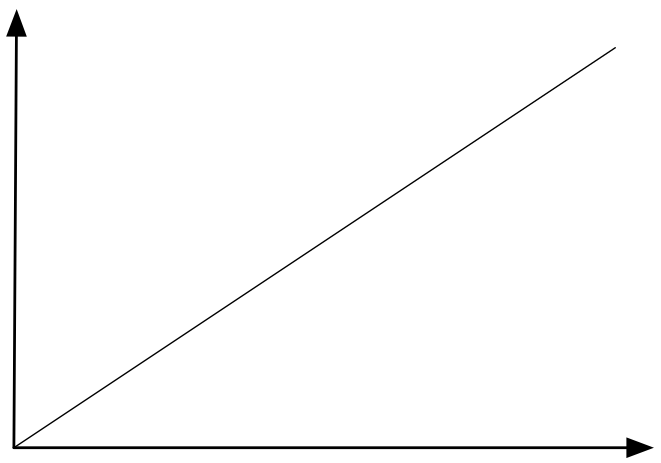
僕「いやいや、早押しクイズじゃないんだから、最後まで問題聞いてほしいな」
問題2
深さが $1$ mで、円筒形をした水槽に水を入れます。
太い管を使って水槽に水を入れると、 $3$ 分で水槽がいっぱいになります。
時刻を $t$ 分とし、 底面から測った水面の位置を $x$ メートルとし、 水面が上がっていく速度を分速 $v$ メートルとする。
時刻 $t$ と速度 $v$ の関係を表すグラフを描きましょう。
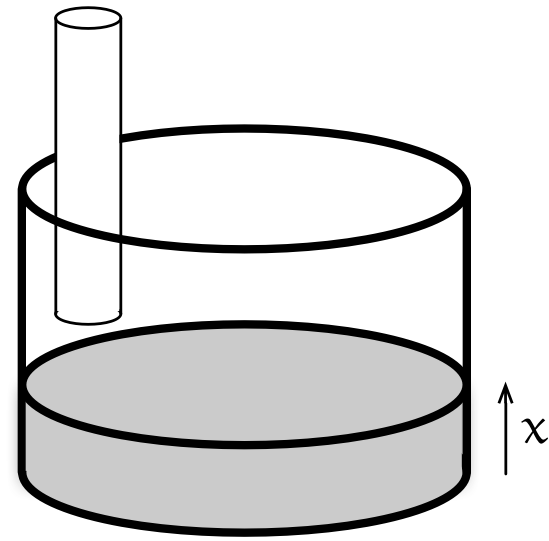
ユーリ「うわずるい! さっきのなし! こーだね!」
解答2
時刻 $t$ と速度 $v$ の関係を表すグラフは以下の通り。
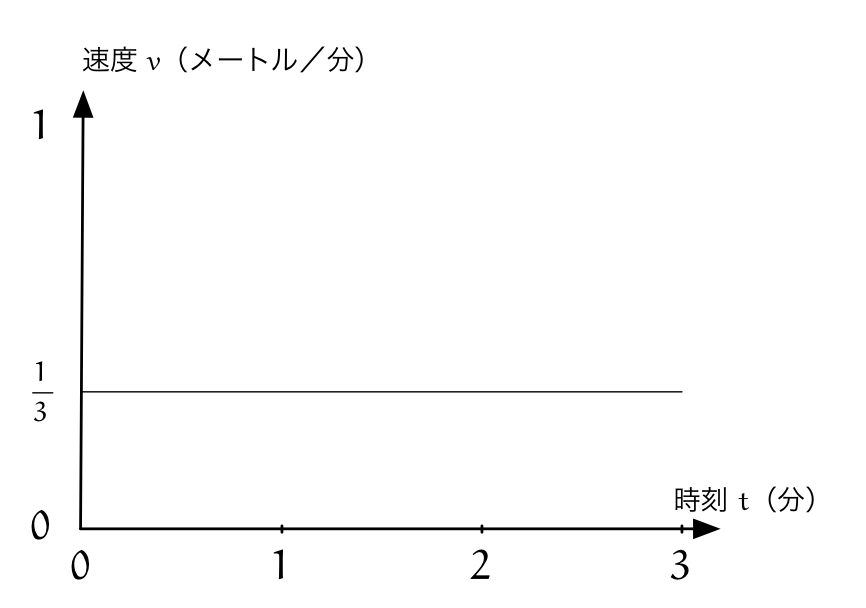
僕「そうだね。時刻と速度の関係を表すグラフなんだから、 ずっと水が増えていくように斜めの線を引いちゃだめだね。 速度はずっと一定で、 $\frac13$ だから」
ユーリ「ふー、あぶなかったぜ」
僕「さっきユーリが描こうとしたのは、 水面が上がる《速度のグラフ》じゃなくて、 水面の《位置のグラフ》だよね」
ユーリ「そだね」
僕「でも、グラフで大事なことを忘れてたよ」
ユーリ「大事なこと……あ、軸?」
僕「そうだよ。グラフでは、軸がなにを表しているかを書かなかったら、 何の意味もない。ただの線になってしまう」
ユーリ「そーだった」
僕「位置のグラフはこうだよね」
時刻 $t$ と位置 $x$ の関係を表すグラフ
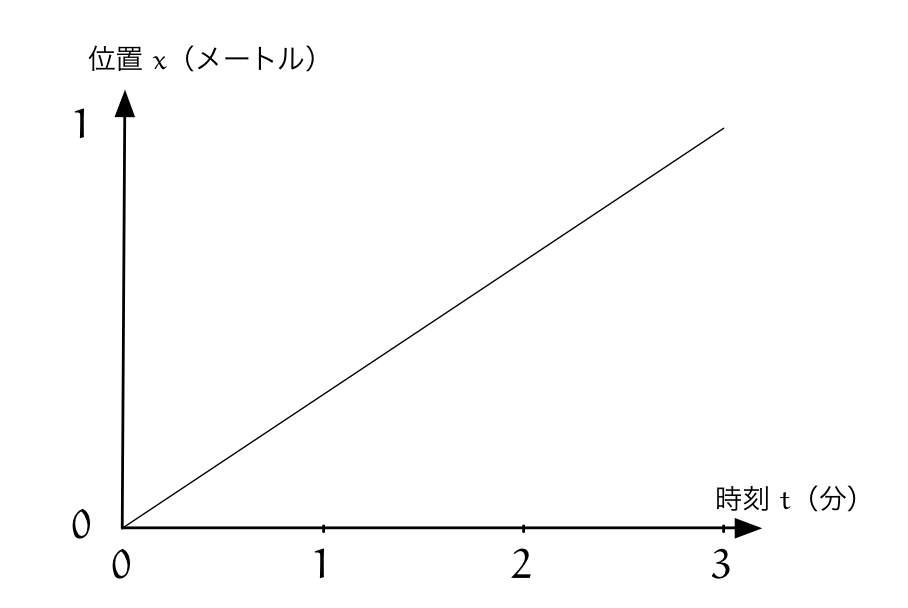
僕「微分の話をしたとき、 《位置のグラフ》から《速度のグラフ》を求めるのは、 ちょうど《時刻で微分する》ことに相当するって話をしたの、覚えてる?」
ユーリ「うん。グラフの傾きでしょ?」
僕「そうだね。この水面の《位置のグラフ》と《速度のグラフ》でも同じことがいえる。 《位置のグラフ》は直線になっていて、その直線の傾きはどこでも $\frac13$ になる。 そしてそれはちょうど《速度のグラフ》がどこでも $\frac13$ という値になっていることを表している」
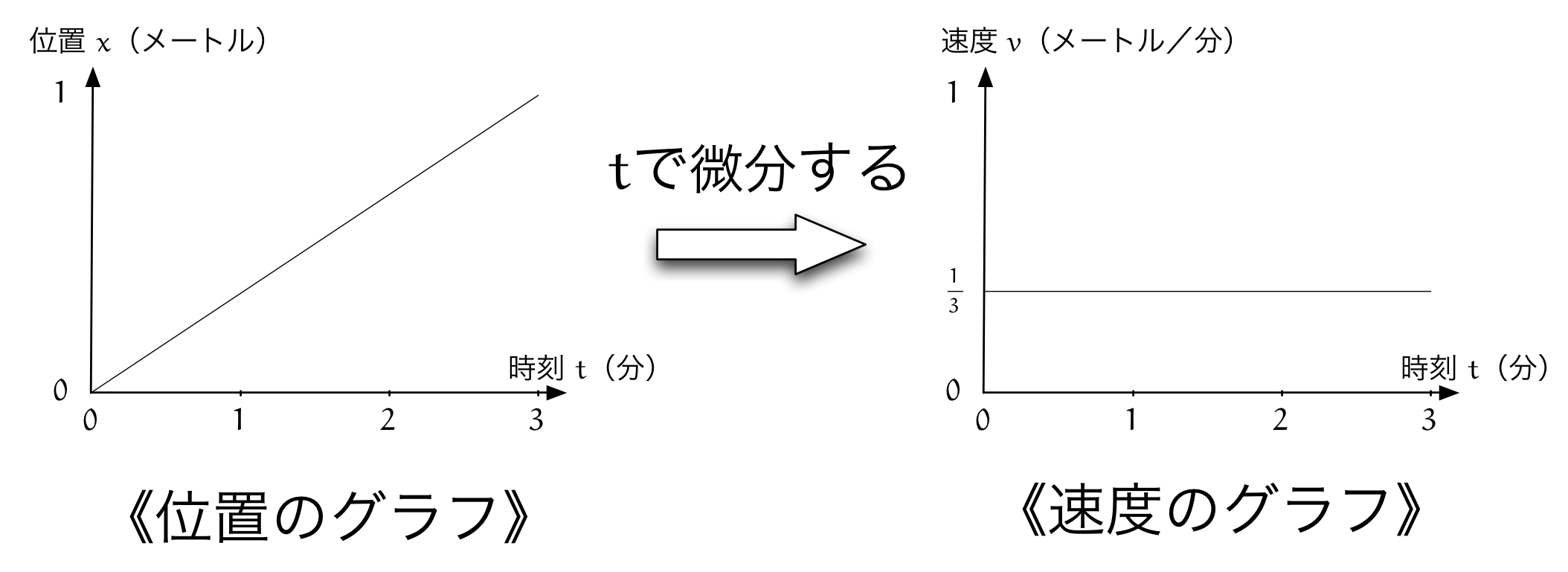
ユーリ「やったやった」
僕「それでね、その《逆》を考えてみよう」
ユーリ「逆って?」
僕「つまり《速度のグラフから位置のグラフを求める》という演算だよ」
ユーリ「ほほー?」
僕「その演算のことを積分というんだ」
ユーリ「せきぶん?」
僕「そう。積分。積分は微分の逆演算。 大ざっぱな言い方をすれば《速度を時刻で積分すると位置を得る》といえる」

ユーリ「積分ってゆーんだ」
僕「それでね、《位置のグラフ》から《速度のグラフ》を求めるとき、 つまり微分するとき、グラフの傾きを求めたよね」
ユーリ「さっきユーリ言ったじゃん」
僕「うんうん、そこで逆だよ。いいかい、ユーリ」
ユーリ「お兄ちゃん、なに前のめりになってんの」
僕「《速度のグラフ》から《位置のグラフ》を求めるとき、 つまり積分するとき、どうしたらいいか。これが問題になる」
問題3
《速度のグラフ》から《位置のグラフ》を求めるには、どうしたらいいか。

ユーリ「そりゃ、グラフの傾きを逆に……」
僕「グラフの傾きを、逆にどうするつもり?」
ユーリ「あり? えーと……っとっと、違うにゃ」
(あなたはもう、気付いていますよね?)
僕「意外に時間がかかるな」
ユーリ「ちがうもん。ちゃんと考えてるだけだもん」
僕「はいはい。それはいいねえ」
ユーリ「あのね。《面積を考えればいい》んじゃない?」
僕「そうだね! たとえば、《速度のグラフ》で $1$ 分、 $2$ 分、 $3$ 分のところまでの面積を考える。 ちょうど《位置のグラフ》はそのときまでの面積をグラフにしたようになる」
《速度のグラフ》が作る面積で《位置のグラフ》を作る
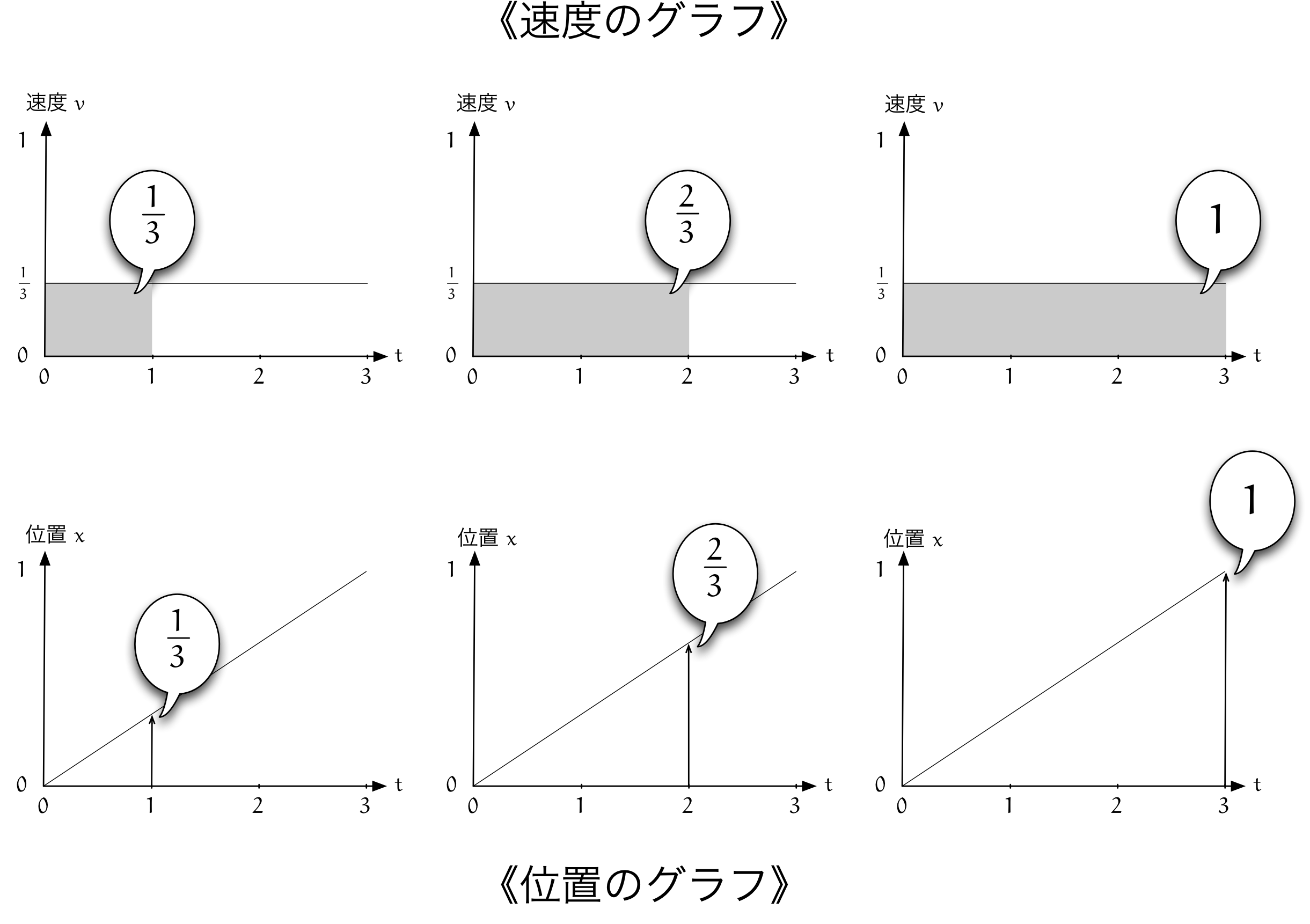
ユーリ「……」
僕「もちろん、それは、 $1$ 分、 $2$ 分、 $3$ 分以外のところでもずっといえる。いくら時刻 $t$ が大きくなってもね」
ユーリ「そこは、ちがうけどね!」
僕「え?」
ユーリ「だって、この水槽の深さは $1$ mなんでしょ?だったら、 $3$ 分過ぎて水がいっぱいになったら、 それ以上水面は高くならないじゃん? あふれちゃうもん!」
僕「あ……そうだね。確かに。深さが $1$ mの水槽ならそうなるな。あふれない範囲において、 《速度のグラフ》が描く面積が《位置のグラフ》を作ることになるね」
ユーリ「しっかりしてよね」
僕「しっかりね……まてよ。さっきの問題は別の点でアバウトすぎたな」
ユーリ「あばうと?」
僕「もっと厳密にいわなきゃいけなかったよ。 つまりね、《速度のグラフ》が描く面積が《位置のグラフ》を作るっていうのは、 《最初に水槽が空っぽのときに限る》からなんだ」
ユーリ「なに言ってるかわかんない」
僕「ほら、さっきの話。《速度のグラフ》の面積で《位置のグラフ》を描いたよね」
ユーリ「あれ、まちがいなの?」
僕「たとえば、最初に水槽が空っぽだったら --- つまり、水面の位置が $0$ mだったなら、 まちがいじゃない。でももしも、水面の位置がたとえば $\frac1{10}$ mつまり $10$ cmなら、 同じ《速度のグラフ》を使っても《位置のグラフ》はこんなふうになるよね」
最初の位置が $\frac1{10}$ mの場合の《位置のグラフ》
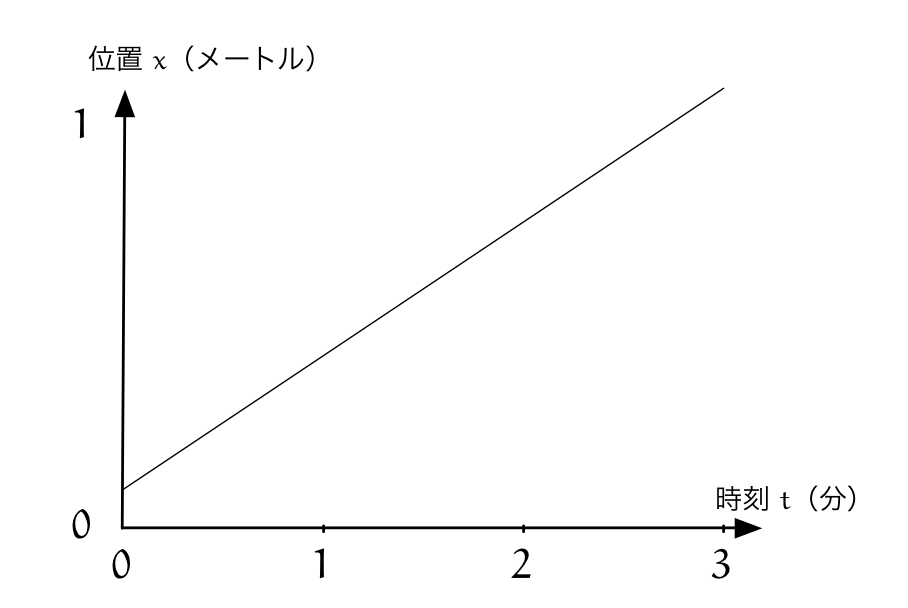
※水槽の深さは $1$ mよりずっと深いものとして考えています。
ユーリ「えーと……あ、そりゃそーじゃん。あったりまえ。 最初 $10$ cmからスタートするからでしょ」
僕「そうそう、そうだね」
ユーリ「だから……最初の水面の位置の分だけ、《位置のグラフ》全体がぐっと上がるだけの話じゃん。 グラフのここんところ」
最初の位置が $\frac1{10}$ mの場合の《位置のグラフ》

僕「その通りだよ。その上がった分のことを積分定数というんだ」
ユーリ「せきぶんていすう?」
僕「そう。積分定数。 ユーリがいうようにあたりまえの話なんだけどね。 《速度のグラフ》だけでは《位置のグラフ》は作れない」
ユーリ「は? さっき、それが積分だって言ったじゃん!」
僕「まあまあ。最初の位置がわからないなら、《速度のグラフ》だけでは《位置のグラフ》は作れない。 でも、最初の位置がわかれば、作れる。そういうこと」
ユーリ「ははあ……」
僕「その最初の位置に相当するのが積分定数なんだよ」
ユーリ「わかったよーな、わかんないよーな」
僕「じゃね、具体的に書いてみよう。《速度のグラフ》を表す数式はこうだよね」
《速度のグラフ》を表す数式
時刻 $t$ での速度を $v$ で表すと、
$$ v = \frac13 $$ となる。
ユーリ「数式ってゆーか、いつでも $v$ は $\frac13$ だってことっしょ?」
僕「そうだね。そして、水槽がはじめに空っぽだった場合の《位置のグラフ》を表す数式はこう」
《位置のグラフ》を表す数式(空っぽからスタート)
時刻 $t$ での位置を $x$ で表すと、
$$ x = \frac13t $$ となる。
ユーリ「あー、ま、そだね。傾きが $\frac13$」
僕「それで、最初の水面の位置を $C$ で表すと、こうなる」
《位置のグラフ》を表す数式(位置 $C$ からスタート)
時刻 $t$ での位置を $x$ で表すと、
$$ x = \frac13t + C $$ となる。
ユーリ「うんうん、そーだね。 $C$ の分だけ、上げたんでしょ?」
僕「その通り。 ここで、速度 $v$ を時刻 $t$ で積分すると位置 $x$ を得る。 つまり、 $\frac13$ を $t$ で積分すると、 $\frac13t + C$ になるんだ。 $C$ を積分定数としてね」
ユーリ「えっ?」
僕「積分は微分の逆演算だから、 微分を使って説明するよ。 ユーリは、簡単な微分を覚えてるかな。 たとえば、 $\frac13t$ を $t$ で微分したら $\frac13$ になる」

ユーリ「うん、それは覚えてるけど……あのね。微分のときって《微分定数》って出てこなかったよね? なんで積分だと《積分定数》 なんて出てくるの?」
僕「それはね……《$\frac13t$ を $t$ で微分したら $\frac13$ になる》というのは正しいんだけど、 微分して $\frac13$ になる関数は $\frac13t$ だけじゃないからなんだよ。 微分して $\frac13$ になる関数は無数にある。 $\frac13t + 1$ も、 $\frac13t + 2$ も、 $\frac13t + 10000$ も……だから、 逆演算として積分を表現するのは難しい」
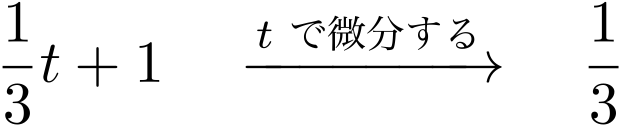
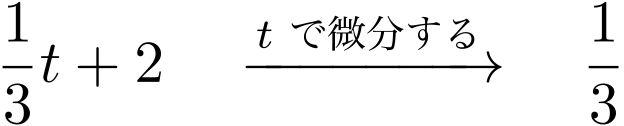
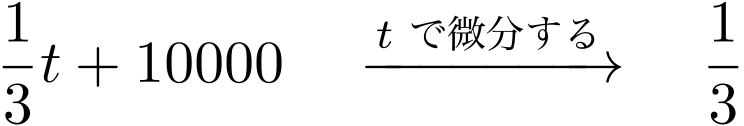
ユーリ「ふんふん?」
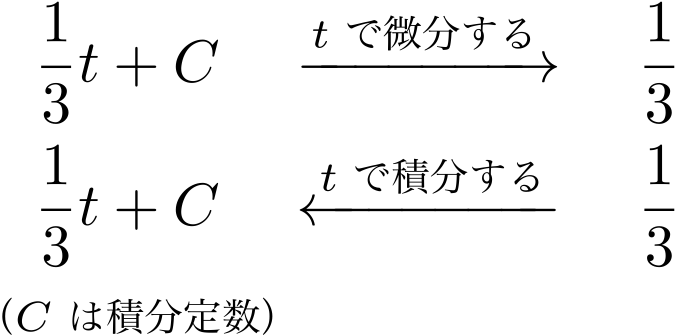
僕「でも、結局ね、無数にあるといっても、定数分だけの違いしかない。 だから、ぜんぶまとめて $C$ としておきましょうっていうことだね。それが積分定数」
ユーリ「ふーん……」
僕「あれ、反応いまいちだな」
ユーリ「あのね、積分定数の話はわかったし、 積分が微分の逆演算ってのもわかったんだけど、 面積って、要するに長方形の面積だし、掛け算すればいいじゃん? それが積分なの? 掛け算が積分?」
僕「なるほど。そこがおもしろいところだよ、ユーリ」
ユーリ「お兄ちゃん、目がきらりんと光ったよ」
この記事は期間限定で「ただいま無料」となっています。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(第131回終わり)
(2015年10月2日)
この記事は『数学ガールの秘密ノート/積分を見つめて』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!