![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/行列が描くもの』として書籍化されています。
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。好奇心旺盛で根気強い《元気少女》。
ミルカさん:数学が好きな高校生。僕のクラスメート。長い黒髪の《饒舌才媛》。
リサ:自在にプログラミングを行う無口な女子。赤い髪の《コンピュータ少女》。
僕とテトラちゃん、それにミルカさんは今日、双倉図書館(ならびくらとしょかん)に集まっている。
ミルカさんの指示でリサがプロジェクタに図形を描いていると、テトラちゃんが平行四辺形について疑問を抱いて……
テトラ「あの……あたし、引っかかることが」
ミルカ「?」
僕「?」
テトラ「以前、先輩からベクトルを教えていただいたとき、 平行四辺形が出てきました(第53回参照)」
ベクトル $\vec a$ と $\vec b$ の和(対角線)
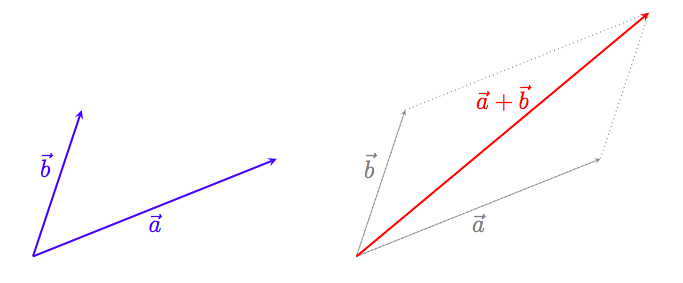
僕「そうだね。ベクトルの和の話」
ミルカ「ふむ」
テトラ「ベクトルの和で平行四辺形が出てきて、行列の変換でも平行四辺形が出てきました。 これには何か意味があるんでしょうか?」
行列 $\left(\begin{array}{cc} 2 & 1 \\ 1 & 3 \end{array} \right)$ で座標平面のマス目を変換する

僕「それはそうだね。ベクトルの和は平行四辺形を作る。 行列で座標平面のマス目を変換すると平行四辺形のマス目になる。 これは同じ話だね」
テトラ「え……でも、あたしは、まだわかっていないようです。 何となくはわかるんですが」
僕「平行移動したベクトル同士は等しいよね。 平行四辺形がベクトルの和に出てくるのはそのため」
テトラ「ええと、あ、はい。わかります。 ベクトル $\vec{a}$ のあとにベクトル $\vec{b}$ をつなげたのが、 ベクトル $\vec{a} + \vec{b}$ だから……ですね?」
ベクトル $\vec a$ と $\vec b$ の和(つなげる)
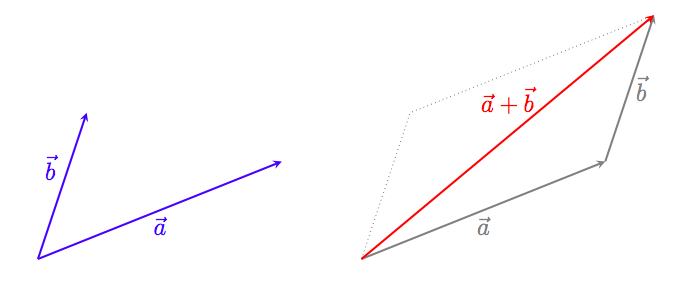
僕「そうそう。ベクトルは平行移動しても変わらないから、 $\vec{b}$ を平行移動させてもかまわない。 だから、ベクトルの和のときに平行四辺形が出てくるんだよね、テトラちゃん」
テトラ「はい、それはわかります」
僕「行列でマス目を変換したときに平行四辺形になるのも同じだよ。 だって、たとえば行列 $\left(\begin{array}{cc} 2 & 1 \\ 1 & 3 \end{array} \right)$ を使えば、 正方形の四頂点を表すベクトル $\VECV00,\VECV10,\VECV01,\VECV11$ は、 それぞれ $\VECV00,\VECV21,\VECV13,\VECV34$ に移るからね」
行列 $\left(\begin{array}{cc} 2 & 1 \\ 1 & 3 \end{array} \right)$ で、正方形の四頂点は平行四辺形の四頂点に移る
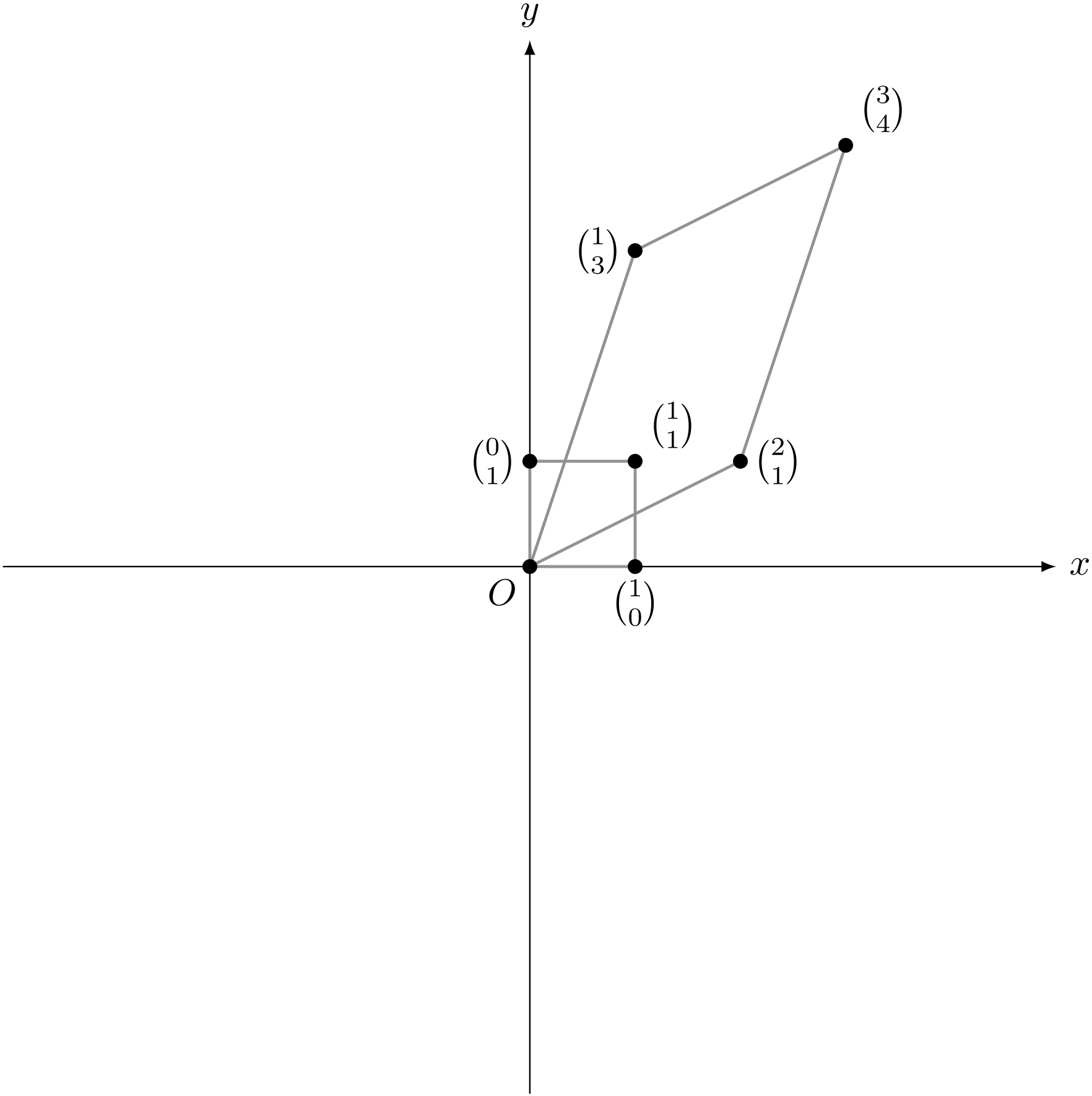
テトラ「は、はあ……」
ミルカ「いや、その説明は言葉足らず」
僕「そう?」
ミルカ「まず、 その説明は $\left(\begin{array}{cc} 2 & 1 \\ 1 & 3 \end{array} \right)$ という一つの行列についてしか語っていない。 それから、《ベクトルの和》と《行列による変換》との関係について語っていない」
僕「うーん……」
ミルカ「 ここは、行列が作り出す変換が線型変換であること、 すなわち《行列による変換の線型性》を語るべきだと思うが」
テトラ「線型性……?」
ミルカ「ベクトルの和を行列で変換し、新たなベクトルを得たとしよう。 そのとき得られるベクトルは、 もとのベクトルを変換して得られるベクトル同士の和になるということ」
テトラ「え、ちょっとお待ちください。ベクトルの……え?」
ミルカ「すなわち、《ベクトルの和を行列で変換すると、 行列で変換したベクトルの和に等しくなる》ということ」
僕「そうか、それを説明すればいいのか。 変換後のベクトルが平行四辺形を作ることになるからだね」
テトラ「す、すみません……あたしは、まだ」
僕「ミルカさんが言ったのは、こういうことだよ。 二つのベクトル $\vec{a}$ と $\vec{b}$ があって、 その和を考える。つまり $\vec{a} + \vec{b}$ というベクトルだね」
テトラ「はい。それはわかります」
僕「たとえば行列を $A$ としたとき、《ベクトルの和を変換したベクトル》 というのは、 $$ A(\vec{a} + \vec{b}) $$ のことだよね」
テトラ「え、えっと」
僕「成分も書いたほうがわかりやすいかな」
ベクトルの和を変換したベクトル
ベクトル $\vec{a}$ とベクトル $\vec{b}$ の和を、行列 $A$ で変換したベクトルは、 $$ A(\vec{a} + \vec{b}) $$ で表される。
たとえば、 $A = \left(\begin{array}{cc} a & b \\ c & d \end{array} \right), \vec{a} = \VECV{a_1}{a_2}, \vec{b} = \VECV{b_1}{b_2}$ とすると、 $$ \left(\begin{array}{cc} a & b \\ c & d \end{array} \right)\VECV{a_1 + b_1}{a_2 + b_2} $$ で表される。具体的には、 $$ \begin{align*} & \left(\begin{array}{cc} a & b \\ c & d \end{array} \right)\VECV{a_1 + b_1}{a_2 + b_2} \\ &= \VECV{a(a_1 + b_1) + b(a_2 + b_2)}{c(a_1 + b_1) + d(a_2 + b_2)} \\ &= \VECV{aa_1 + ab_1 + ba_2 + bb_2}{ca_1 + cb_1 + da_2 + db_2} \\ \end{align*} $$ になる。
テトラ「あ、そういう意味ですね。 《ベクトルを行列で変換する》というのは《行列とベクトルの積》ですから、 行列と、和で表されているベクトルとの積を取る……」
僕「そうそう。 それでね、ミルカさんが言ってたもう一つ《ベクトルを変換したベクトルの和》というのは、 $\vec{a}$ と $\vec{b}$ のそれぞれを行列で変換してから、その後で和を取るという意味なんだよ。 つまり、 $A\vec{a} + A\vec{b}$ のこと」
ベクトルを変換したベクトルの和
ベクトル $\vec{a}$ を行列 $A$ で線型変換したベクトルと、 ベクトル $\vec{b}$ を行列 $A$ で線型変換したベクトルの和は、 $$ A\vec{a} + A\vec{b} $$ で表される。
たとえば、 $A = \left(\begin{array}{cc} a & b \\ c & d \end{array} \right), \vec{a} = \VECV{a_1}{a_2}, \vec{b} = \VECV{b_1}{b_2}$ とすると、 $$ \left(\begin{array}{cc} a & b \\ c & d \end{array} \right)\VECV{a_1}{a_2} + \left(\begin{array}{cc} a & b \\ c & d \end{array} \right)\VECV{b_1}{b_2} $$ で表される。具体的には、 $$ \begin{align*} & \left(\begin{array}{cc} a & b \\ c & d \end{array} \right)\VECV{a_1}{a_2} + \left(\begin{array}{cc} a & b \\ c & d \end{array} \right)\VECV{b_1}{b_2} \\ &= \VECV{aa_1 + ba_2}{ca_1 + da_2} + \VECV{ab_1 + bb_2}{cb_1 + db_2} \\ &= \VECV{aa_1 + ba_2 + ab_1 + bb_2}{ca_1 + da_2 + cb_1 + db_2} \\ \end{align*} $$ になる。
僕「そして、この両者は等しくなるんだ!」
行列による変換の線型性 $$ A(\vec{a} + \vec{b}) = A\vec{a} + A\vec{b} $$
行列による変換の線型性(成分表示) $$ \begin{align*} \left(\begin{array}{cc} a & b \\ c & d \end{array} \right)\VECV{a_1+b_1}{a_2+b_2} &= \left(\begin{array}{cc} a & b \\ c & d \end{array} \right)\VECV{a_1}{a_2} + \left(\begin{array}{cc} a & b \\ c & d \end{array} \right)\VECV{b_1}{b_2} \\ \VECV{aa_1 + ab_1 + ba_2 + bb_2}{ca_1 + cb_1 + da_2 + db_2} &= \VECV{aa_1 + ba_2 + ab_1 + bb_2}{ca_1 + da_2 + cb_1 + db_2} \\ \end{align*} $$
テトラ「……」
僕「納得行かない? 成分表示をよく見ればわかるよね」
テトラ「いえ、すみません。違うんです。 これって、すごいことなんでしょうか? あたしには、 何だかあたりまえのように思えるんですけれど」
僕「まあ、あたりまえといえば、あたりまえだけど」
テトラ「ちがうんです。いえ、ちがわないんですけど。 たとえば、 $$ A(\vec{a} + \vec{b}) = A\vec{a} + A\vec{b} $$ という式なんですが、 これは何というか《分配法則》のようなことが成り立つということですよね。 そう言われれば、そういうのが成り立ってもおかしくないなあと思いますし、 きっと証明もできるんだと思うんですが、 というか、さきほどの成分計算で、成分を比較すれば証明になっているんだと思うんです。それはいいんです。 でも、さっきまで、平行四辺形の話題が進んでいましたよね。 どうして、急にこの分配法則の話になっちゃったんですか? ミルカさんと先輩はその理由がおわかりになっているようです。 でも、あたしにはそのつながりがわからないです。 つまりですね。あたしにはこの式は……この式が成り立つことは、 あたりまえのように思えますけれど、 それがどういうふうに平行四辺形と関係しているのかがわかってないんです。 す、すみません。ものわかりが悪くて」
リサ「饒舌テトラ」
僕「……」
ミルカ「変換前、二つのベクトル $\vec{a} = \VECV{a}{0}$ と $\vec{b} = \VECV{0}{b}$ は、長方形を作る。 $\VECV00, \VECV{a}{0}, \VECV{0}{b}, \VECV{a}{b}$ の四点。四つ目の点は《ベクトルの和》$\vec{a} + \vec{b}$ だ。 四つ目の点がベクトルの和で作られているから、平行四辺形になっている」
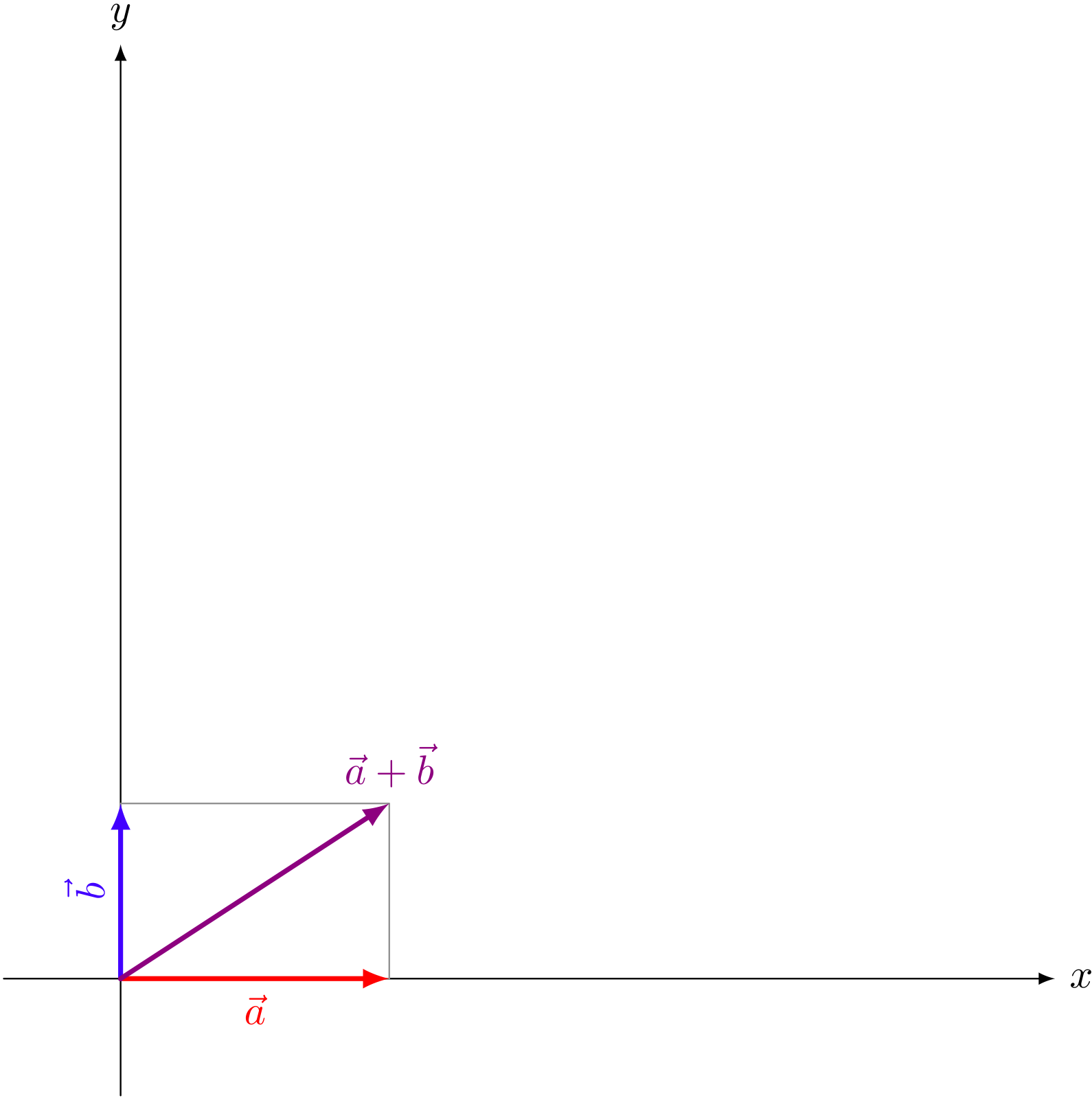
テトラ「はい、大丈夫です。長方形も平行四辺形の一種ですから」
ミルカ「では変換後、 $\vec{a}$ と、 $\vec{b}$ と、そして、この《ベクトルの和 $\vec{a} + \vec{b}$》はどんなベクトルに移るだろうか?」
テトラ「ベクトルの和が、どんなベクトルに移るか……」
ミルカ「そう。 $\vec{a}$ は $A\vec{a}$ に移り、 $\vec{b}$ は $A\vec{b}$ に移る。 では、 $\vec{a} + \vec{b}$ はどこに移るだろうか」
テトラ「ははあ……わかります。 $A(\vec{a} + \vec{b})$ に移りますね」
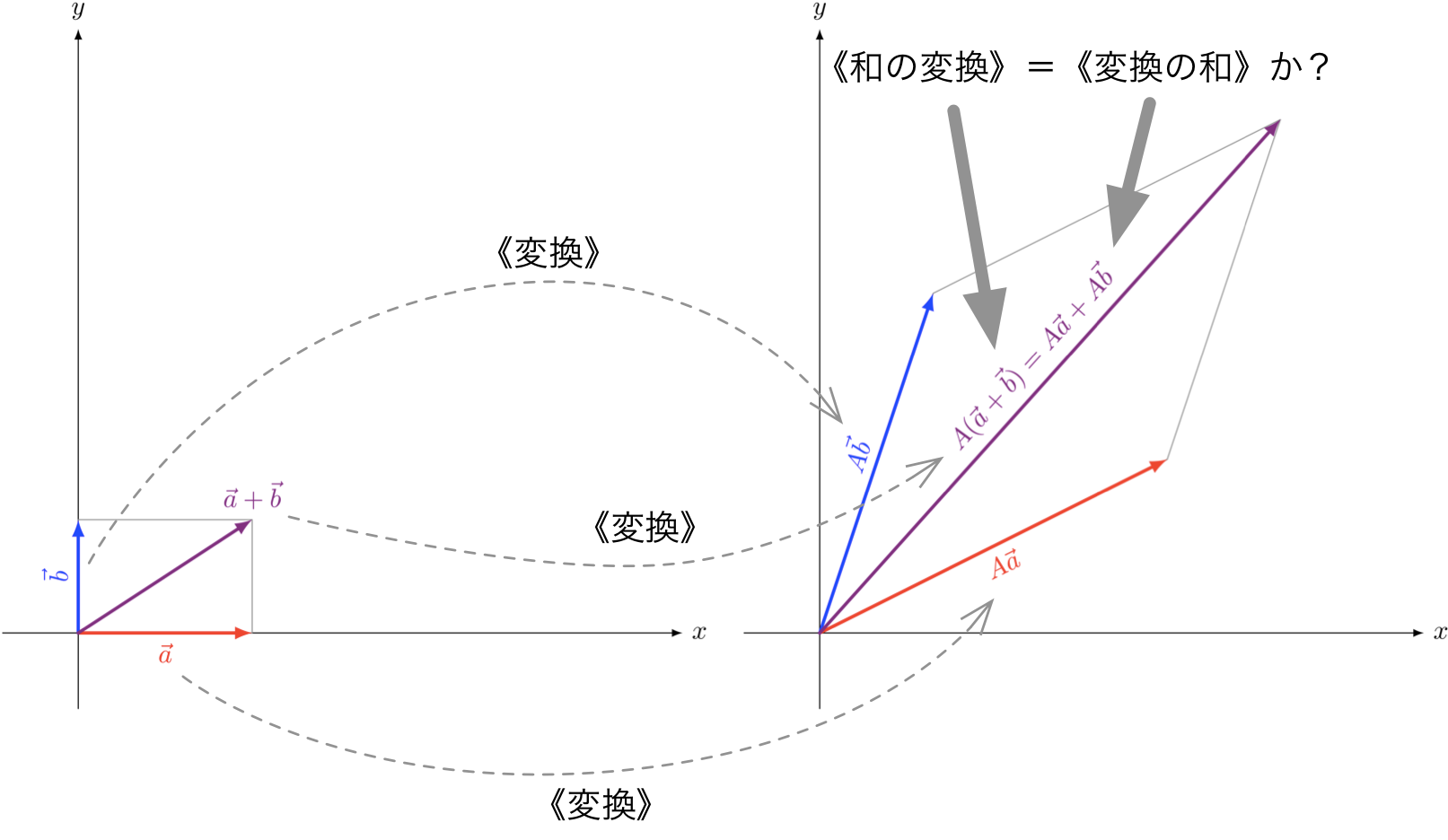
ミルカ「そうだ。 《和を変換したベクトル》は $A(\vec{a} + \vec{b})$ になる。 そして、《変換したベクトルの和》は《$A\vec{a}$ と $A\vec{b}$ の和》すなわち $A\vec{a} + A\vec{b}$ になる。 この両者は等しいかな? つまり、 《和を変換したベクトル》は、《変換したベクトルの和》になるかな? 《和の変換》と《変換の和》。 もしも、この二つが一致するなら−−−テトラは、ベクトルの和が 平行四辺形を生み出すことを知っているのだから−−−行列による変換が平行四辺形のマス目を生み出すことも納得できるのではないかな?」
テトラ「!」
僕「わかった?」
テトラ「わかりました! あ、あれれ? あたし、なんでこんなこと、すぐわからなかったんでしょう!」
ミルカ「線型性は数学のあちこちに出てくる。 すべて、《和の○○は、○○の和》として表現できる。 こんなふうに」
微分の線型性
《和の微分は、微分の和》
$$ \left(f(x) + g(x)\right)' = f'(x) + g'(x) $$
積分の線型性
《和の積分は、積分の和》
$$ \int_{a}^{b} \left(f(x) + g(x)\right)dx = \int_{a}^{b} f(x) dx + \int_{a}^{b} g(x) dx $$
期待値の線型性
《和の期待値は、期待値の和》 $$ E[X + Y] = E[X] + E[Y] $$
行列による変換の線型性
《和の変換は、変換の和》
$$ A(\vec{a} + \vec{b}) = A\vec{a} + A\vec{b} $$
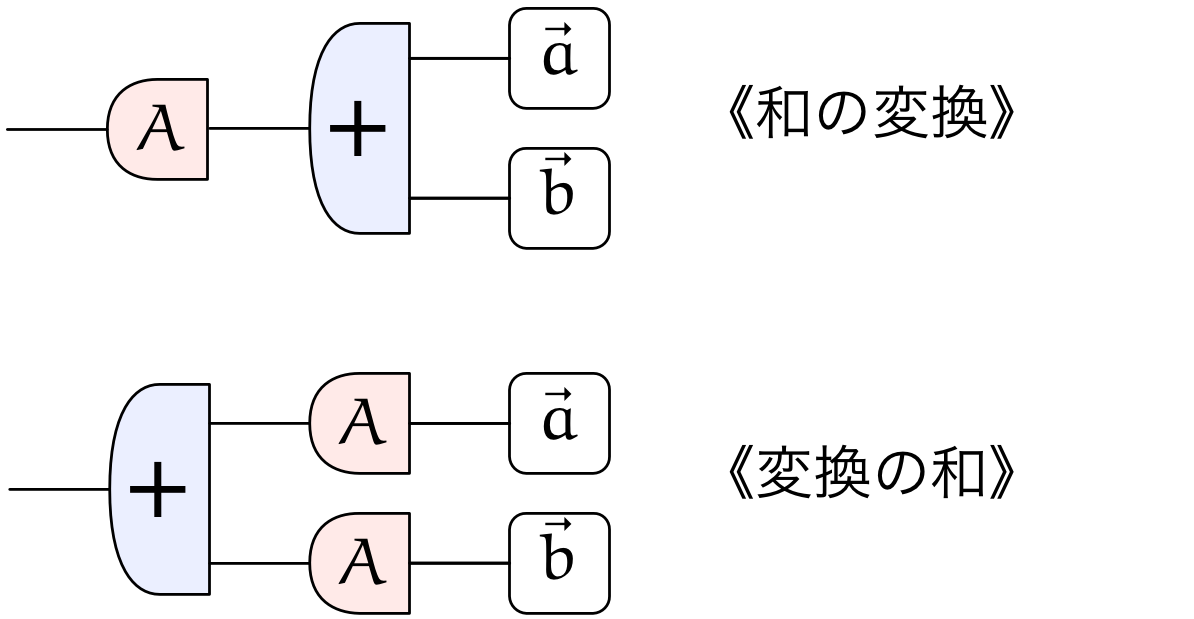
リサ「演算装置の交換」
行列による変換の線型性を演算装置の交換で表現
ミルカ「ふむ、なるほど」
おしゃべりが一段落してから、テトラちゃんが改めて話し始めた。
テトラ「リサちゃん、行列 $\left(\begin{array}{cc} 2 & 1 \\ 1 & 3 \end{array} \right)$ の変換の様子をもう一度表示してもらえますか」
リサ「《ちゃん》は不要」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2015年5月22日)
この記事は『数学ガールの秘密ノート/行列が描くもの』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!