第117回 シーズン12 エピソード7

星空トランスフォーム（前編）

双倉図書館

テトラ「リサちゃんの発表、あたしには難しかったみたいです」

リサ「《ちゃん》は不要」

ミルカ「今回は、大半がマニア向けの話だったような」

リサ「全部が」

テトラ「あ、でも、コンピュータグラフィクスの星空はきれいでした！　あんなのが作れるってすごいです！」

僕「確かにきれいだったよね。あそこから星座の話にもってくるのか、という」

リサ「普通」

テトラ「ああいうプログラムって、難しいんでしょうね……」

リサ「基本は簡単」

ミルカ「簡単なものを基本という。大量の行列計算？」

リサ「ライブラリで一発」

テトラ「行列？　行列がプログラムに出てくるんですか？」

僕「なるほど。座標の計算をすることになるからか」

ミルカ「お茶が済んだら、リサに簡単なデモをしてもらおう。行列計算の基本」

行列計算の基本

リサ「ミルカ氏が解説」

ミルカ「ふむ。まずは、座標平面上に点を打つことにしよう。テトラが点の座標を言う」

テトラ「ど、どこでもいいんですか？　それでは、先手のあたしは、点 $(2,1)$ で」

僕「テトラちゃん……囲碁将棋じゃないんだから」

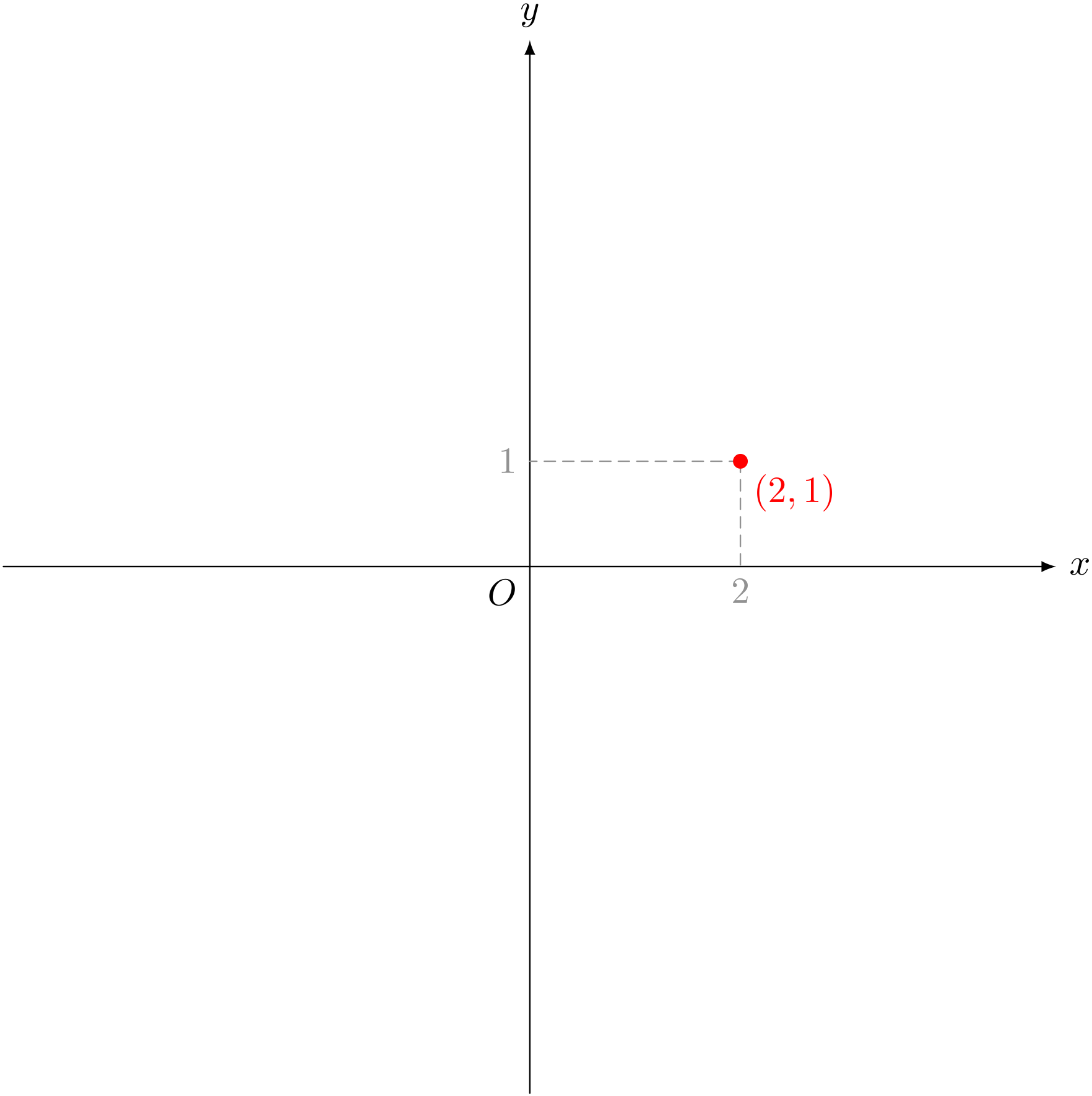
僕「まあ、確かに点 $(2,1)$ だよね」

ミルカ「$x$ 座標と $y$ 座標が決まれば、点が一つ決まる。 だから、ヴェクタを使って……縦ベクトルを使って $\VECV21$ と書いてもかまわない」

ミルカ「そしてここで適当な行列を決めよう。君が決める」

僕「え、適当に決めていいの？」

ミルカ「いい。センスが問われるけれど」

僕「（何のセンスなんだろう）じゃあ、とりあえず簡単なもので……たとえば、 $\left(\begin{array}{cc} 2 & 0 \\ 0 & 2 \end{array} \right)$」

ミルカ「その行列 $\left(\begin{array}{cc} 2 & 0 \\ 0 & 2 \end{array} \right)$ と、点を表しているこの縦ベクトル $\VECV21$ との積を計算すれば $\VECV42$ になる」

テトラ「ちょ、ちょっと待ってください。確認なんですが、 《行列と縦ベクトルの積》というのは、 行列の積と同じような計算をするんですよね。 《掛けて、掛けて、足す》です」

ミルカ「もちろん」

テトラ「すみません、話の腰を折ってしまいました」

ミルカ「行列 $\left(\begin{array}{cc} 2 & 0 \\ 0 & 2 \end{array} \right)$ と縦ベクトル $\VECV21$ を掛けて、 縦ベクトル $\VECV42$ を得た。 もちろんこの縦ベクトル $\VECV42$ も座標平面上の点 $(4,2)$ と見なせる」

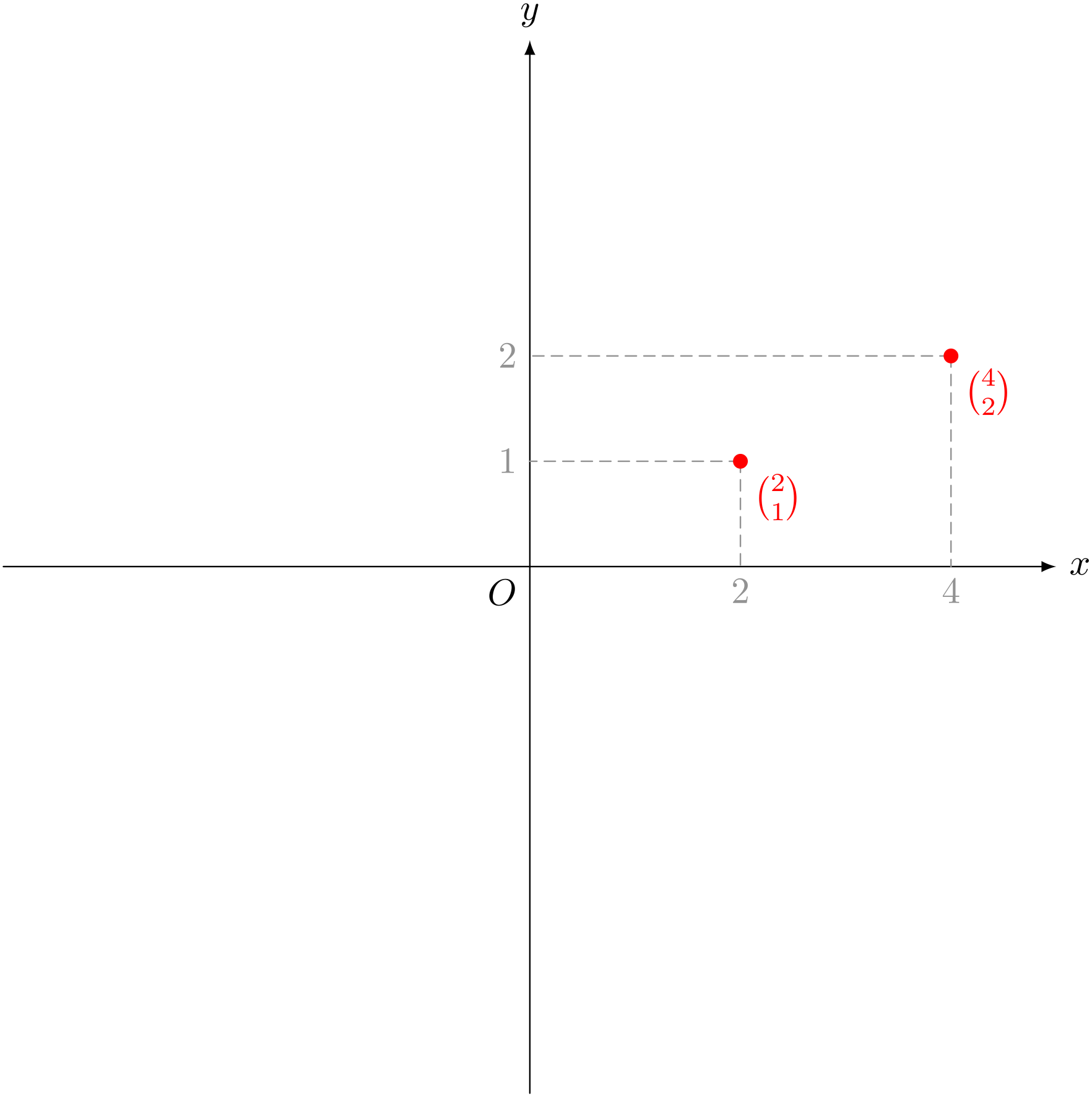
テトラ「そうですね」

ミルカ「こんなふうにも言える。 すなわち、 $\left(\begin{array}{cc} 2 & 0 \\ 0 & 2 \end{array} \right)$ という行列は、点 $(2,1)$ を点 $(4,2)$ に移す」

テトラ「移す……」

ミルカ「リサ、矢印出る？」

リサ「当然」

テトラ「……」

僕「行列が変われば、点が移る先も変わるよね。 たとえば、 $\left(\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array} \right)$ という行列とか」

リサ「いま出す」

テトラ「え、ええっと。あ、そうですね。計算すればすぐに出ます」

テトラ「あ……でも、考えてみれば当たり前です。 だって、点は $x$ と $y$ で決まりますよね。 行列と縦ベクトルの積を取ったら、 $x$ や $y$ の値は変化します。 それで点が動くというのは当たり前……ですよね？」

ミルカ「その通り。しかし、ここで自然な疑問が浮かんでくる」

テトラ「疑問……」

ミルカ「君が答える」

僕「それはもちろん……ひとつの行列が与えられたとき、 《この行列は、どんなふうに点を移すのか？》 という疑問だよね」

テトラ「え？　でも、それは根気よく計算すればいい話ではないんでしょうか。 行列の積の方法はわかっています。ですから、行列が与えられれば、 点がどこに移されるかはわかりますよね。計算すれば」

リサ「あるいはプログラムで」

僕「もちろんそうだよ、テトラちゃん。計算すれば具体的にわかる。 でも、行列はその形を見るだけで、どんな変換を行うかわかるんだ。 パターンがあるんだよ」

テトラ「そうなんですか。……変換？」

ミルカ「$2\times2$ の行列は座標平面上の点を移す。それを、その行列がおこなう変換という。 正確には《一次変換》あるいは《線型変換》という」

テトラ「はあ……」

ミルカ「さっきは一点だけを移動した。行列がおこなう変換を見るために、 もっとたくさんの点を移してみよう。リサはすぐ出せるかな」

リサ「曖昧な指示」

ミルカ「しかし応えるリサ」

テトラ「きゃああっ！　……失礼しました。びっくりしてしまいました」

僕「たくさん出たなあ」

ミルカ「多すぎる。象限ごとに点の描き方も変えて」

リサ「仕様変更」

ミルカ「しかし応えるリサ」

僕「なるほど。一辺が $1$ の……いや、一辺が $2$ の正方形だね」

テトラ「この点を全部、行列を使って変換するわけですね」

ミルカ「たとえば、 $\left(\begin{array}{cc} 2 & 0 \\ 0 & 2 \end{array} \right)$ で変換した後」

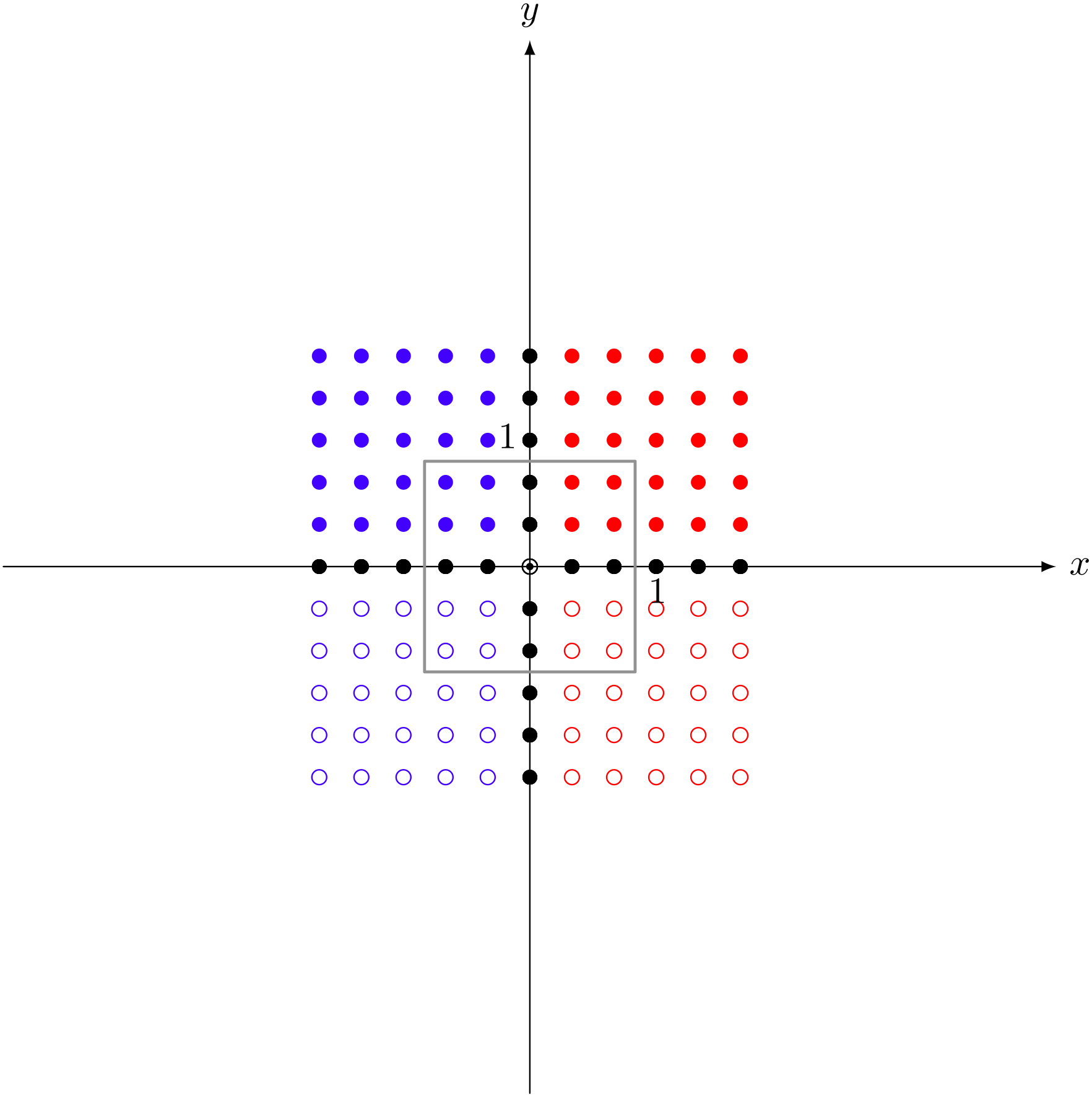
ミルカ「矢印でも出せるかな」

リサ「要求過多」

ミルカ「しかし応えるリサ」

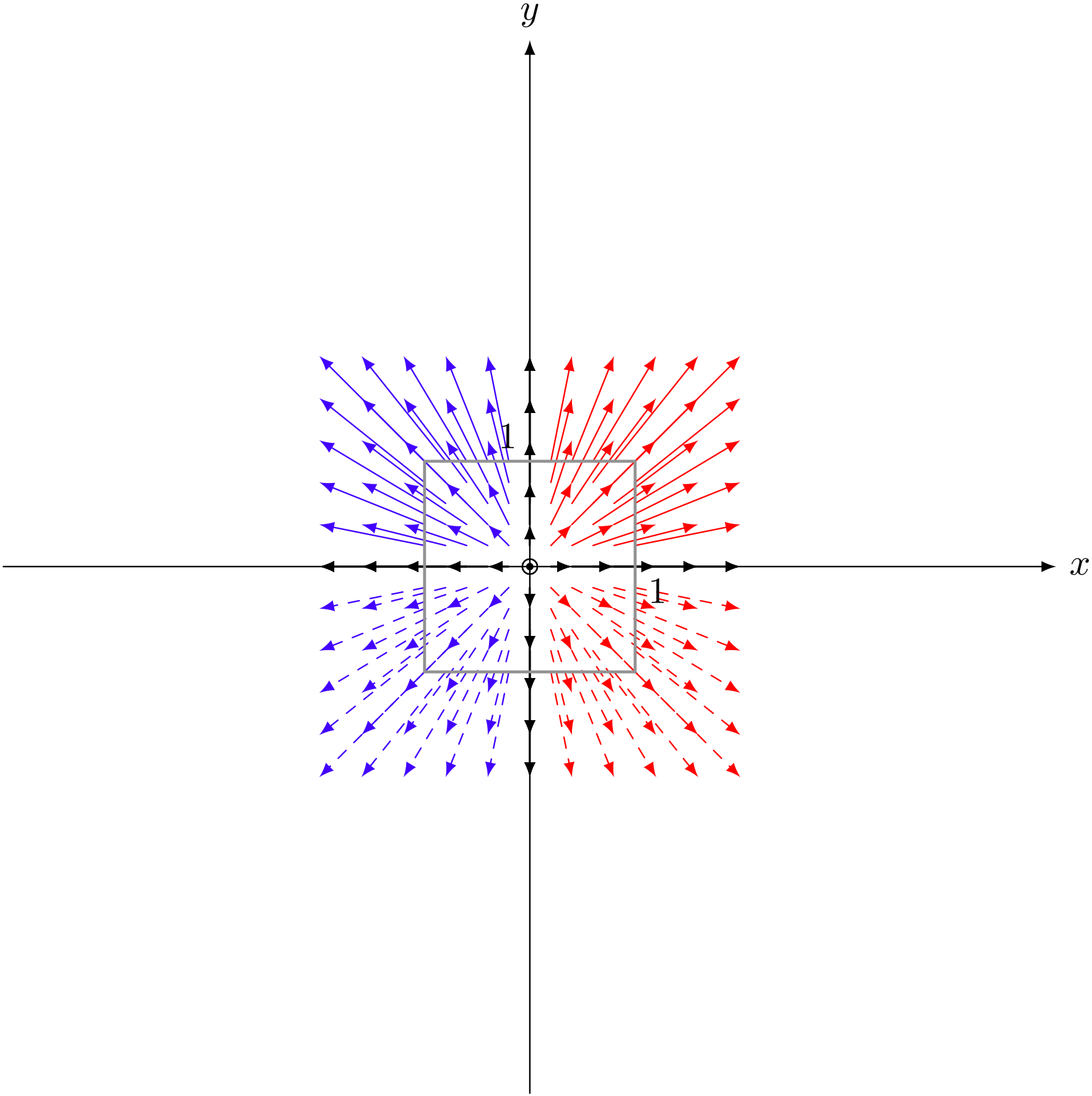
テトラ「なるほどです！　点がわあっと広がって」

僕「$\left(\begin{array}{cc} 2 & 0 \\ 0 & 2 \end{array} \right)$ は $2I$ だからね」

テトラ「$2I$ ……ということは、 $2\left(\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right)$ ということですね。 ははあ、だから $2$ 倍に！　これもまた《たとえ話》です。 《行列の世界》の $\left(\begin{array}{cc} 2 & 0 \\ 0 & 2 \end{array} \right)$ は、《数の世界》の $2$ のたとえ話みたいです」

僕「点が広がる様子は、一般的な点 $(x,y)$ がどこに移動するかを見ればわかりやすいよ。 つまり、縦ベクトル $\VECV{x}{y}$ がどういう縦ベクトルに変換されるか」

テトラ「わかりました。 $x$ 座標も $y$ 座標も、どちらも $2$ 倍になっているから、あのようにわあっと広がったわけですね。 むむ……ということはですよ。もしかして、 $\frac12I = \left(\begin{array}{cc} \frac12 & 0 \\ 0 & \frac12 \end{array} \right)$ を使えば、きゅうっと縮むんでしょうか」

リサ「$0.5$ を使った」

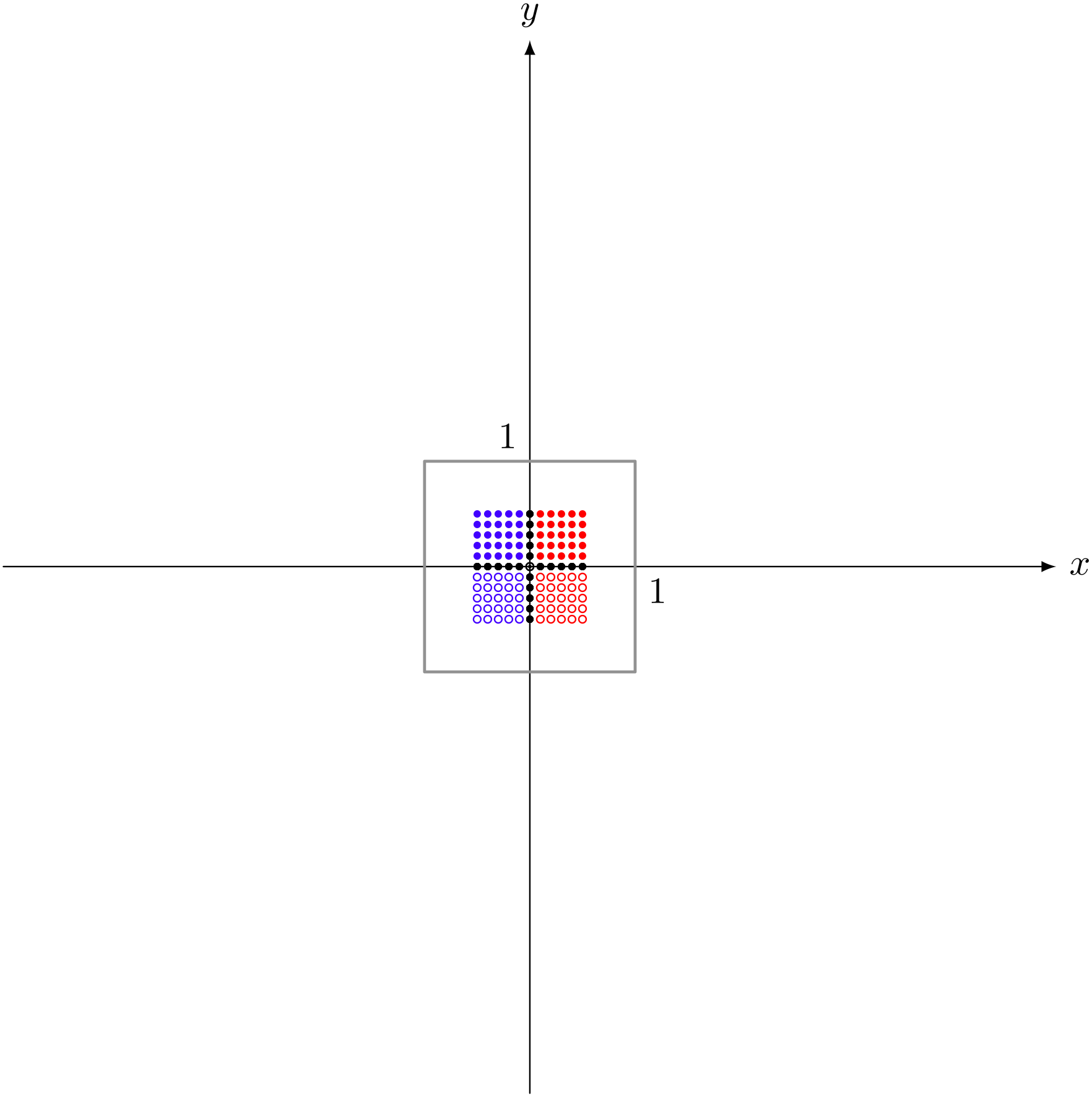
テトラ「なるほどです。 $2I$ なら広がって、 $\frac12I$ なら縮んで、そして単位行列 $I$ ならばそのままですね、きっと」

リサ「単位行列」

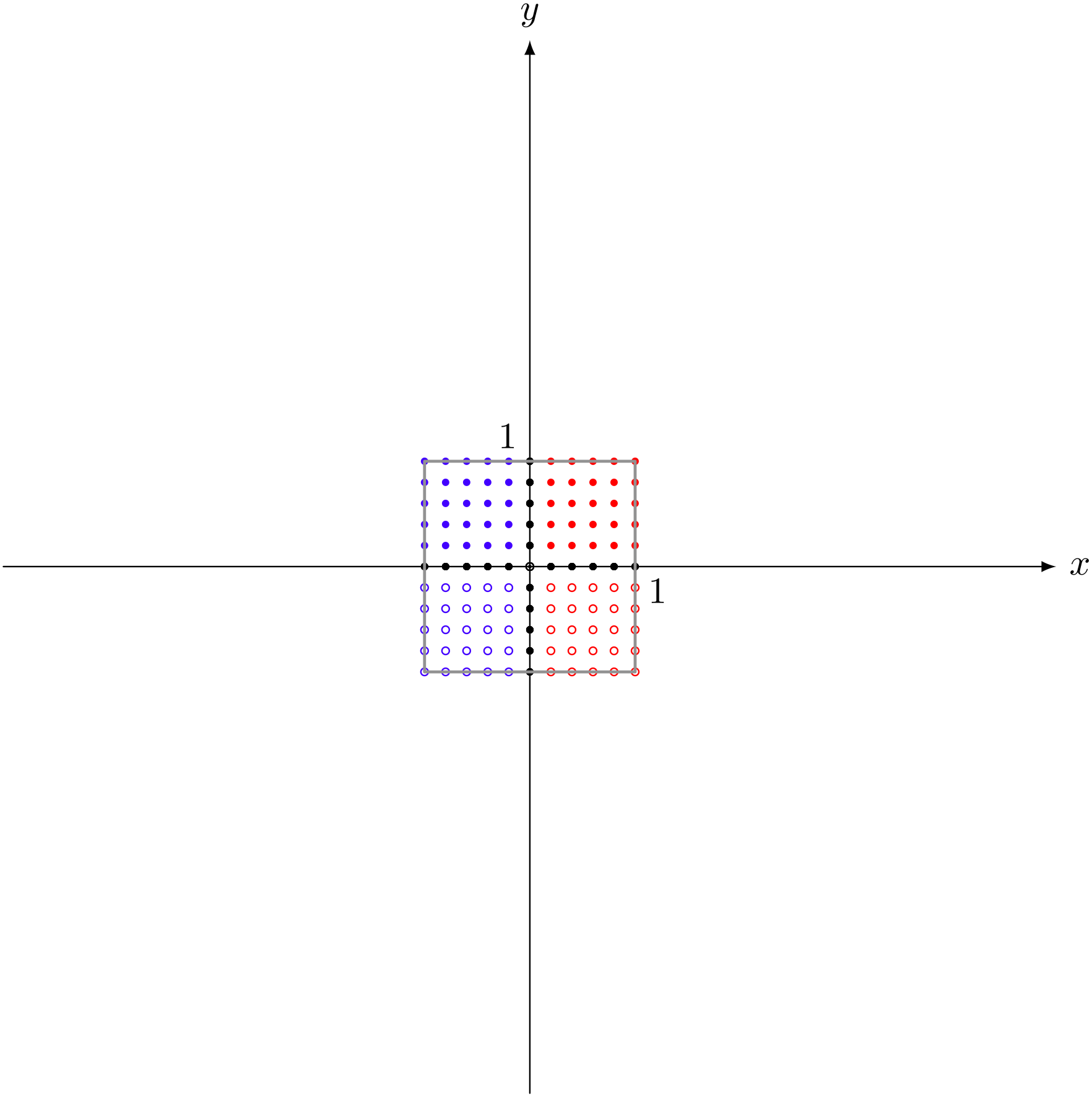
テトラ「パターンという意味が少しわかりました。たとえば、 $a$ という文字を使って、 $\left(\begin{array}{cc} a & 0 \\ 0 & a \end{array} \right)$ という形をした行列を作れば、ちょうど $a$ 倍だけ広がることになるんですね」

僕「そうだね。 $\left(\begin{array}{cc} a & 0 \\ 0 & a \end{array} \right)$ は原点を中心にして拡大する変換になるね。 $a > 1$ なら広がるし、 $0 < a < 1$ なら縮むし、 $a = 0$ なら……」

テトラ「ああ、 $a = 0$ なら、 $\left(\begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array} \right)$ ですから、原点につぶれてしまいますね！」

僕「うんうん」

別の行列

ミルカ「$a \neq b$ の行列を試してみよう。 たとえば、 $\left(\begin{array}{cc} 3 & 0 \\ 0 & 2 \end{array} \right)$ はどんな変換になるか。リサ？」

リサ「表示開始」

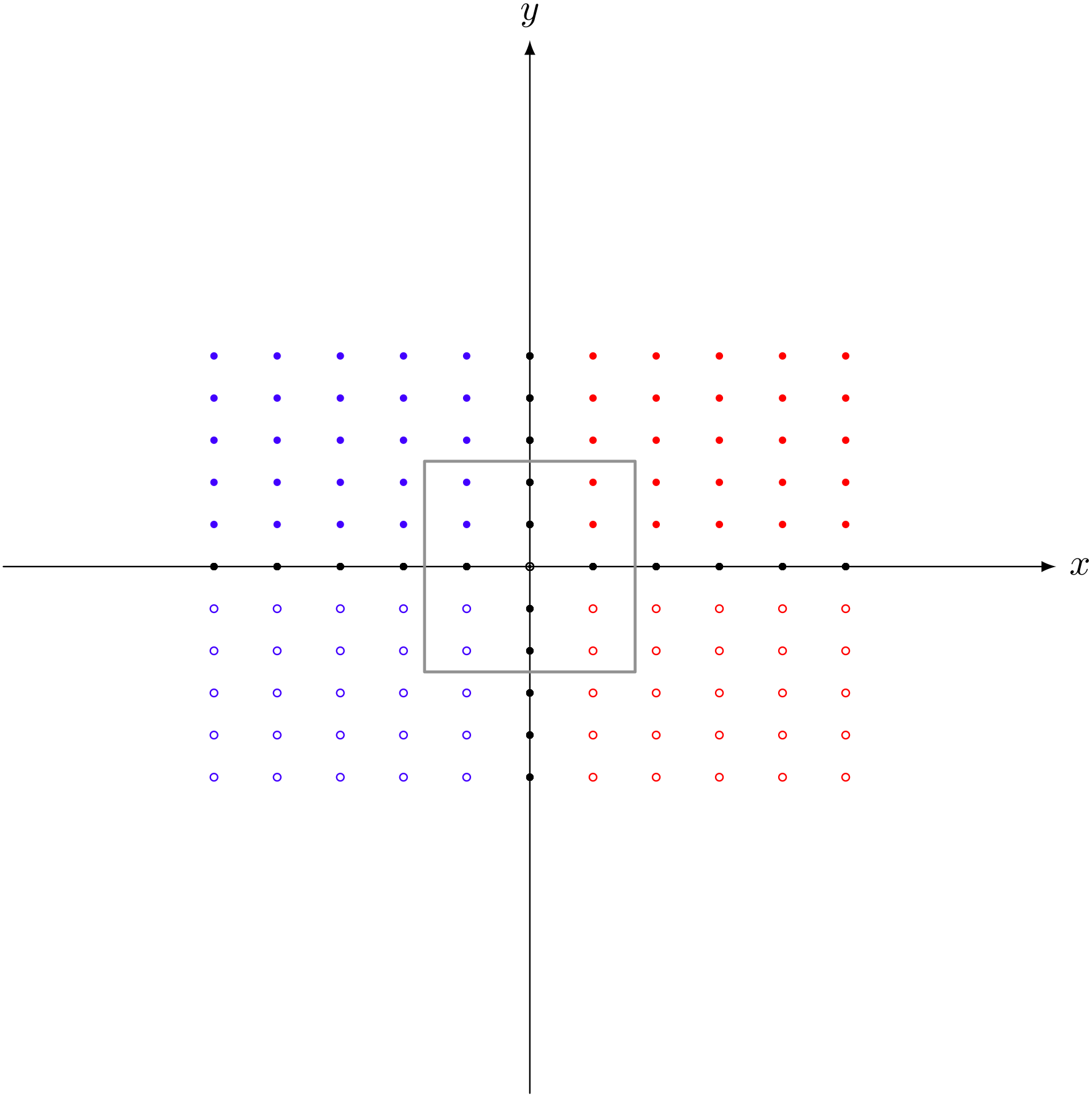
テトラ「なるほどです。横方向には $3$ 倍で、縦方向には $2$ 倍ですね……」

僕「数と違うところだね。《方向》によって変えられる」

さらに別の行列

ミルカ「別の行列を試してみよう。 たとえば、そうだな。 $\left(\begin{array}{cc} 2 & 1 \\ 1 & 3 \end{array} \right)$ でやってみよう。 リサ、表示はストップ。 テトラ、どんな形が現れると思う？」