![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/行列が描くもの』として書籍化されています。
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。僕のことを《お兄ちゃん》と呼ぶ。
ユーリと僕は《行列》について話している。
僕「これで、行列の相等($=$)と和($+$)と差($-$)が定義できて、 零行列 $\left(\begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array} \right)$ も定義できたね(第111回参照)。 つまり、これで、等しいかどうかを調べることと、 足し算と、引き算ができる《数のようなもの》を作ったことになる。 ゼロも作った」
ユーリ「にゃるほど。ねえ、じゃ、次は? 次は何を作るの?」
僕「それはもちろん、アレだよ」
ユーリ「そっかー、アレかー……アレって何?」
僕「行列の世界で《$0$ に相当するもの》として零行列を作ったから、 次は《$1$ に相当するもの》を作ろう」
ユーリ「ゼロ行列じゃなくて、イチ行列?」
僕「壱行列とは言わなくて、ふつうは単位行列というよ」
ユーリ「たんいぎょうれつ……これは簡単だよね。 成分をぜんぶ $1$ にすればいいんでしょ?」
これが単位行列なの?
$$ \left(\begin{array}{cc} 1 & 1 \\ 1 & 1 \end{array} \right) $$
僕「ユーリは、どうしてそう思ったんだろうか」
ユーリ「お兄ちゃんは、どーしてそー聞き返したんだろーか」
僕「何?」
ユーリ「いや、今回の聞き返しはユーリがまちがったから? それとも、 ほんとに理由を聞きたいから?」
僕「その両方」
ユーリ「え、 $\left(\begin{array}{cc} 1 & 1 \\ 1 & 1 \end{array} \right)$ はまちがいなの?」
僕「うん、残念ながら、それは単位行列じゃない」
ユーリ「だって、零行列のときは成分が全部 $0$ だったじゃん?」
僕「そうだね」
零行列はすべての成分が $0$
$$ \left(\begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array} \right) $$
ユーリ「だったら、単位行列は $1$ みたいなものなんだから、 成分が全部 $1$ になるんじゃないの?」
僕「そこだよ。そこで重要な問いかけが出てくる。 さっきは『ゼロって何だろう』という問いかけだった(第111回参照)。 今度は『イチって何だろう』という問いかけになる」
ユーリ「ゼロは、足しても変わらないものだった。イチは、足したら $1$ 増えるものでしょ?」
僕「うん、そう考えることも可能だね。 そしてそう考えると、ユーリが $\left(\begin{array}{cc} 1 & 1 \\ 1 & 1 \end{array} \right)$ をイチにしたくなる理由もわかる。 $\left(\begin{array}{cc} 1 & 1 \\ 1 & 1 \end{array} \right)$ を加えると、行列の成分がぜんぶ $1$ 増えるから」
$$ \left(\begin{array}{cc} a & b \\ c & d \end{array} \right) + \left(\begin{array}{cc} 1 & 1 \\ 1 & 1 \end{array} \right) = \left(\begin{array}{cc} a+1 & b+1 \\ c+1 & d+1 \end{array} \right) $$ユーリ「そー考えたんだけど」
僕「そう考えることももちろん可能だよ。 でも、それは少しつまらないともいえる。 それだと、行列が数と同じふるまいしかしなくなるから」
ユーリ「じゃあ、何がイチなの?」
僕「こんなふうに考えてみよう。 《どんな数にゼロを足しても変わらない》と同じようにして、 《どんな数にイチを掛けても変わらない》というふうにね」
ユーリ「ほほー! なーるほど。足し算じゃなくて掛け算?」
《ゼロとイチ》(数の場合)
$$ \begin{align*} a + 0 &= a && \REMTEXT{どんな数にゼロを足しても変わらない} \\ a \times 1 &= a && \REMTEXT{どんな数にイチを掛けても変わらない} \\ \end{align*} $$
僕「そうだね。こんなふうにも言える。《足し算にとってのゼロ》は、 《掛け算にとってのイチ》」
ユーリ「お兄ちゃん、ちょっとかっこいい……あれ?、ちょっと待ってよ。 《掛け算にとってのイチ》はいーんだけど、 それだったらユーリがさっき答えた $\left(\begin{array}{cc} 1 & 1 \\ 1 & 1 \end{array} \right)$ で正解じゃん? だって、 成分に $1$ を掛けたら変わらないよ?」
僕「あ、いやいや、そうじゃないんだよ。 行列の積は成分ごとの積じゃないんだ。 行列の掛け算……行列の積はまだ定義してなかった」
ユーリ「じゃ、早く定義して!」
僕「二つの行列 $\left(\begin{array}{cc} a & b \\ c & d \end{array} \right)$ と $\left(\begin{array}{cc} s & t \\ u & v \end{array} \right)$ があったと考えよう」
ユーリ「考えたくない」
僕「がく。何を言い出すやら」
ユーリ「お兄ちゃんは数式のまじゅちゅち……まずちゅし……数式の魔法使いだからいーかもしれないけど」
僕「魔術師」
ユーリ「数式の魔法使いだからいーかもしれないけど、 いきなり $a,b,c,d,s,t,u,v$ とかやめてほしー」
僕「やめてほしいといわれても……わかった。じゃあ、こうしよう。 二つの行列 $\left(\begin{array}{cc} a & b \\ c & d \end{array} \right)$ と $\left(\begin{array}{cc} a' & b' \\ c' & d' \end{array} \right)$ があったと考えよう。 $a,b,c,d$ と $a',b',c',d'$ はぜんぶ何らかの数だよ」
二つの行列
$$ \left(\begin{array}{cc} a & b \\ c & d \end{array} \right) \quad \REMTEXT{と} \quad \left(\begin{array}{cc} a' & b' \\ c' & d' \end{array} \right) $$
ユーリ「うん。これならなんとか」
僕「それはよかった。この二つの行列の積を、こんな式で定義する。 二つの行列を並べて積を表すよ」
行列の積を定義する
$$ \left(\begin{array}{cc} a & b \\ c & d \end{array} \right)\left(\begin{array}{cc} a' & b' \\ c' & d' \end{array} \right) = \left(\begin{array}{cc} aa'+bc' & ab'+bd' \\ ca'+dc' & cb'+dd' \end{array} \right) $$
ユーリ「うわ、手加減なしかー。何この式のラレツ!」
僕「定義に手加減もなにもないよ。 いっぺんに全部みるとわけがわからなくなるから、 成分を一つ一つ見てみよう。まず、これ」
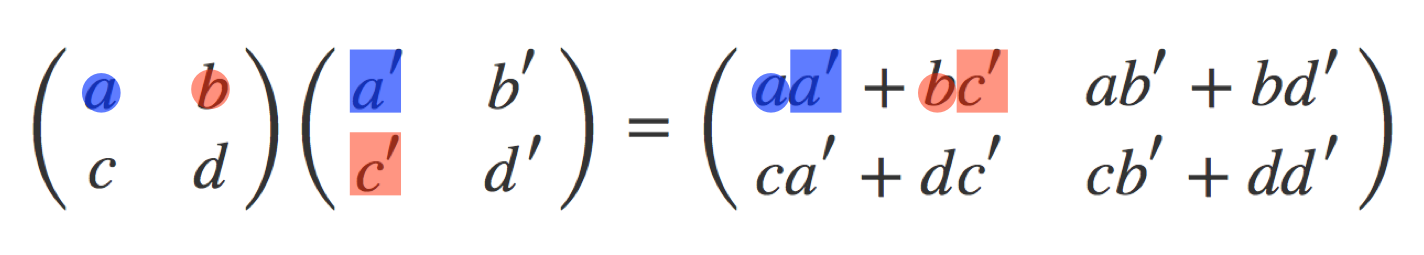
ユーリ「ははー。 $a$ と $a'$ を掛けて、 $b$ と $c'$ を掛けてる……?」
僕「そうだね。そして $aa'$ と $bc'$ を足す。 行列の積で基本になる計算は《掛けて、掛けて、足す》という計算だよ。 ここでは、 $aa' + bc'$ に《掛けて、掛けて、足す》という形が出ているね」
$aa'+bc'$ の《掛けて、掛けて、足す》
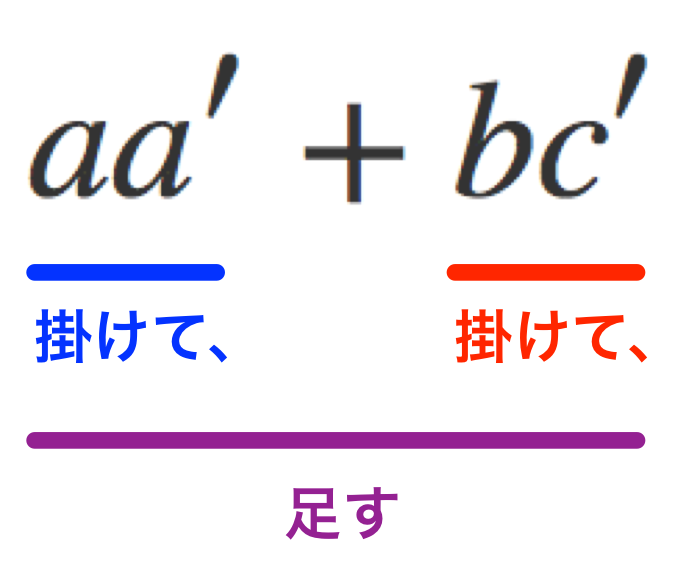
ユーリ「《掛けて、掛けて、足す》……ふんふん?」
僕「二つの行列を掛けたときに、左側の行列では《行》をまとまりとして見る。 右側の行列では《列》をまとまりとして見る。 そして、成分同士について《掛けて、掛けて、足す》という計算をするんだよ」
$aa'+bc'$ がどうやってできたか
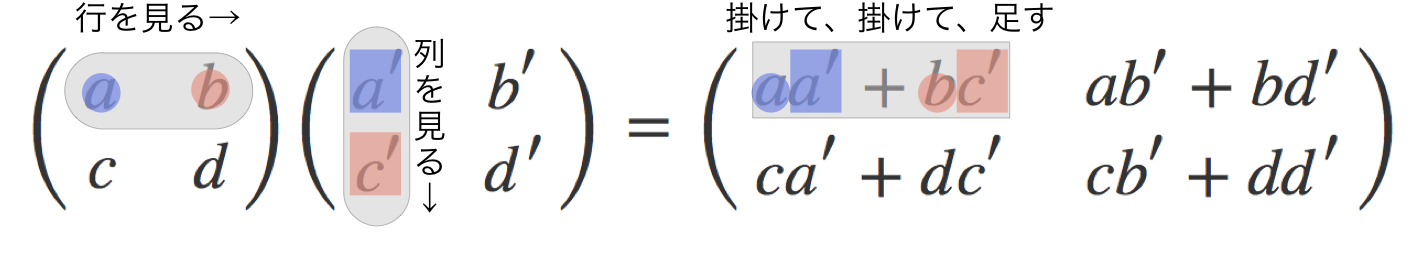
ユーリ「……ふふーん、だいぶ《見えて》きたよ」
僕「それはすごいな。お兄ちゃんは、行列の積を初めて見たとき、この計算に慣れるまで時間が掛かったよ」
ユーリ「左目を横に動かして、右目を縦に動かして見れば、簡単だもん!」
僕「いやいや、それは人間には無理だから!」
僕「他の成分もまったく同じに考える。たとえば、 $ab'+bd'$ はこうやって計算する」
$ab'+bd'$ がどうやってできたか
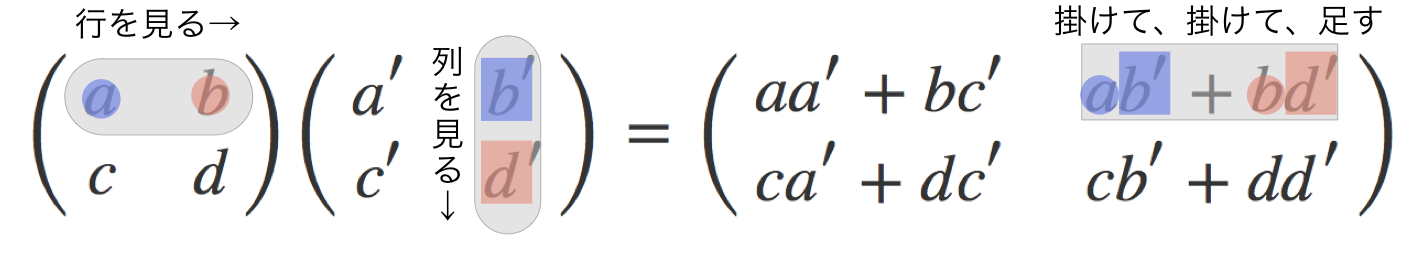
ユーリ「ほんとだ……でたらめに式を書いたんじゃなかったんだね!」
僕「そりゃそうだよ。次に $ca'+dc'$ はこうだよ」
$ca'+dc'$ がどうやってできたか

ユーリ「もーわかったよ」
僕「そして、最後に $cb'+dd'$ はこう」
$cb'+dd'$ がどうやってできたか

ユーリ「わかったって!」
僕「じゃ、試しに計算してみようか。行列の掛け算練習」
問題
次に示す行列の積を計算してみよう。
$$ \left(\begin{array}{cc} 1 & 2 \\ 3 & 4 \end{array} \right)\left(\begin{array}{cc} 1 & 3 \\ 2 & 0 \end{array} \right) $$
ユーリ「掛けて、掛けて、足す……」
(あなたも、やってみましょう!)

僕「どう? できた?」
ユーリ「できたできた。目と頭がごちゃごちゃしてきた」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2015年4月10日)
この記事は『数学ガールの秘密ノート/行列が描くもの』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!